Решение задачи фильтрования суспензий при наложении пульсационных колебаний давления

SOLUTION OF THE PROBLEM OF FILTERING SUSPENSIONS AT SUPERVISION OF PULSATION PRESSURE OSCILLATIONS

Usmonali Saidullaev

Samarkand State University, Uzbekistan, Samarkand

Murodzhon Shoimov

Samarkand State University, Uzbekistan, Samarkand

Jurabek Khuzhakulov

Samarkand State University, Uzbekistan, Samarkand

Shokhrukh Boliev

Samarkand State University, Uzbekistan, Samarkand

Isomiddin Nishonov

Samarkand State University, Uzbekistan, Samarkand

Аннотация. В работе дается решение задачи фильтрования суспензий с учетом явлений конвективного переноса и переменного роста слоя осадка на поверхности фильтра. Математическая модель фильтрования реализована численно. Установлено влияние коэффициента консолидации и конвективных эффектов на характеристики фильтрования.

Abstract. In the paper a suspensions filtering problem with convective transport of particles and variable deposit layer growth on the filter surface is considered. Corresponding mathematical model of the process is numerically realized. Influence of deposit layer consolidation and convective transport effects on filtering characteristics is established.

Ключевая слова: суспензия; фильтрование; кейк-слой; задача Стефена.

Keywords: suspension; filtration; cake; a Stefan problem.

Рассмотрим одномерную задачу процесса фильтрование на базе уравнение консолидации осадка с учетом влияние пульсационных колебаний давления на сжимаемость осадка.

Процесс состоит в следующем: имеется плоский фильтровальный элемент. Суспензия должна соприкасаться с первоначально имеющимся фильтрующим слоем. Под действием разности давлений, которая является периодически изменяющейся во времени, начинается процесс разделения суспензии. Периодически увеличивается и толщина осадка . В данном случае координата осадка направлена противоположна движению суспензии.

Математическая модель фильтрования, записанная относительно гидродинамического давления выглядит следующим образом [1,2,3]:

,                                                   (1)

 ,                                                          (2)

 ,                                                          (3)

 ,     ,                                           (4)

Для одновременного учета роста слоя осадка используется уравнение перемещения границы раздела осадок-суспензия

.                                             (5)

В уравнениях (1)-(5) - поровое давление;  − давление жидкости в начальный момент времени;  - давление на входе в слой осадка;  - давление на выходе из фильтрующего слоя (фильтрующий слой составляет осадок и исходный фильтрующий слой); - вязкость жидкости; - удельное сопротивление осадка; - коэффициент наружного отложения осадка;  − коэффициент консолидации, характеризующий реакцию сжимаемого осадка на внешнее поле давлений, , -модуль сжимаемости осадка;

Вводя новую переменную [1,4]

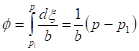
получим

.                                                                    (6)

Тогда уравнение (1) преобразуется к виду

 .                                                                   (7)

После преобразования условий (2) - (5) приходим к виду

,                                                    (8)

,                                                    (9)

 ,    ,                                                (10)

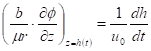 .                                                     (11)

Для численного решения задачи (7) − (11) будем пользовать неравномерную сетку по пространственной переменной [4,5]. Новые узлы этой сетки будем определять из условия, что в этот узел попадает граница раздела осадок-суспензия. В области  построим сетку по правилу:   где  − шаг по пространственной переменной ;  − количество узлов на временном отрезке ;  − шаг по времени. - величина, определяющая сдвиг границы раздела осадок-суспензия за временной промежуток , .

Для решения задачи (7) – (11) составляем следующую разностную схему:

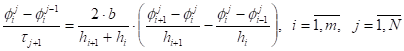.             (12)

Аппроксимация начального и граничных условий (8)-(10) дает

,                                                                 (13)

,                                                                 (14)

.                                                                  (15)

Для аппроксимации условия (11) используем простейшее разностное соотношение

.                                       (16)

Разностная задача (12) - (16) аппроксимирует дифференциальную задачу (7)-(11) с точностью .

Для решения задачи (12)-(16) по определению  и  применим метод прогонки [4,5].

Уравнение (12) приводится к виду

,  

и решение ищется в виде

,  ,   .

Для прогоночных коэффициентов используются следующие формулы

, , ,

, ,  .

Здесь

, , , .

Все коэффициенты  и  вычисляются до . Принимая во внимание граничные условия (15)-(16), приходим к кубическому уравнению для определения 

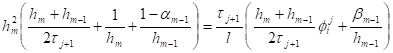
где .

Численные результаты решения задачи (12) - (16) получены при следующих значениях параметров: МПа, МПа, м²с^-1, м^-2, , , .

По результатом численных расчетов построены графики зависимости давления (Рис.1) и толщины осадка от времени (Рис.2). Из Рис.1 видно, что с течением времени давление увеличивается периодически. Толщина осадка (Рис.2) изменяется так же. Необходимо отметить, что характеристики фильтрования зависят от амплитудно-частотных характеристик колебания давления. Используя указанный алгоритм можно оценить различные режимы фильтрования для широкого диапазона изменения амплитуд и частот колебания давления.

Список литературы: