Приближённое вычисление корней многочлена

Аннотация: В данной статье рассматривается вопрос о понятие многочленах и приближенное вычисление корней многочлена. методы вычисления корней многочленов.

Ключевые слова: Многочлен, Методы вычисления корней многочленов, Метод Ньютона, Метод хорд, Метод Лобачевского.

Общий вид уравнения  n-й степени (где n – некоторое целое положительное число) есть:

Коэффициенты  a₀ ,  a₁ ,  a₂ , a_n-1 ,  a_n  , этого уравнения мы будем считать произвольными комплексными числами, причём старший коэффициент a₀ должен быть отличен от нуля.

Если написано уравнение (1), то всегда предполагается, что требуется его решить, т. е. требуется найти такое числовое значение для неизвестного x, которое удовлетворяет этому уравнению и после подстановки вместо неизвестного и выполнения всех указанных операций обращает левую часть уравнения (1) в нуль.

Целесообразно, заменить задачу решения уравнения (1) задачей нахождения корней левой части этого уравнения:

  , называемом многочленом.

Действительные корни любого алгебраического уравнения с действительными коэффициентами могут быть найдены с любой точностью [1] путём вычисления значений многочлена в отдельных точках. Покажем это на примере. Многочлен 

имеет корень в интервале (1;2). Обозначим этот корень через х₀ . вычисляя значения f(x) в точках 1,1 ; 1,2 ; … 1,9 , мы обнаружим, что

f(1,2) < 0        ,   f(1,3)>0   ,

следовательно х₀  лежит в интервале (1,2 ; 1,3). Вычисляя значения f(x) в точках 1,21 , 1,22 , … 1,29 , находим , что

f(1,24) < 0     ,    f(1,25)> 0 .

следовательно, х₀  лежит в интервале (1,24 ; 1,25) .

Таким образом мы можем найти любое количество десятичных знаков искомого корня х₀ , т. е. вычислить его с любой наперёд заданной точностью.

Существуют гораздо более совершенные методы: метод Ньютона, метод итераций,  метод Лобачевского и др.

Первый метод: Метод линейной интерполяции

Данный метод иногда называют методом ложного положения. В качестве приближенного значения корня можно принять полусумму границ a и b   , т.е. середину отрезка, концы которого и есть точки . Вполне естественно предположить, что корень лежит ближе к той из границ , которой соответствует меньшее по абсолютной величине значение многочлена. Метод линейной интерполяции состоит в том, что в качестве приближенного значения корня α берётся число с, которое делит отрезок (a, b) на части, пропорциональные абсолютным величинам чисел f(a) f(b):

;

Знак минус в правой части поставлен потому, что f(a) и  f(b) имеют разные знаки. Преобразуя, получим:

                                                                                                                (1)

Как видно из рисунка 2, геометрически метод линейной интерполяции заключается в том, что на отрезке () кривая y=f(x) заменяется её хордой (отсюда ещё одно название данного метода – метод хорд), соединяющий точки A(a,f(a)) и B(b,f(b)). В качестве приближенного значения корня α принимается абсцисса точки пересечения этой хорды с осью х.

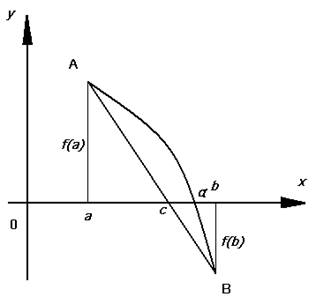
Рисунок 2. Метод хорд

Метод Ньютона

Мы имеем α – простой корень многочлена f(x), тогда  f ^'(α)≠0. Примем также, что и f  ^''(α)≠0, в противном случае вопрос сводится к вычислению корня многочлена f  ''(x), имеющего меньшую степень, чем f(x). Примем также, что отрезок (a, b) не содержит корней f(x), отличных от α, но и не содержит ни корня многочлена f ^'(x),а также и корня многочлена f ''(x).

В таком случае функция y = f(x) на отрезке (a, b) либо монотонно возрастает, либо монотонно убывает, а также во всех точках этого промежутка выпукла вверх или выпукла вниз. В расположенной прямой могут встретится четыре случая, представленных на рис 3-8. Обозначим через а₀ тот из пределов a и b, в котором знак f(x) совпадают со знаком  f ''(x). Так как f(a) и f(b) имеют разные знаки, а f ^''(x) сохраняет знак на всем отрезке (a, b), то такое a₀ может было указано. В случаях, представленных на рис. 3 и 4,

будет a₀ = a, в двух других случаях a₀ = b. В точке кривой y = f(x) с абсциссой a₀ , т.е. в точке с координатами (a₀ , f(a₀)), проведём касательную к этой кривой и обозначим через d абсциссу точки пересечения этой касательной с осью х. Рисунки 3-6 показывают, что число d можно считать приближенным значением корня α. [2]

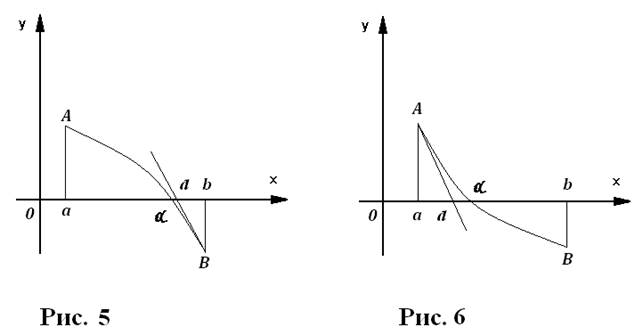
Метод Ньютона состоит, следовательно, в замене кривой y = f(x) на отрезке (a, b) её касательной в одной из границ этого отрезка. Условие, наложенное на выбор точки a₀ , очень существенно: рис. 7 показывает, что без соблюдения этого условия точка пересечения касательной с осью х может совсем не давать приближения к искомому корню.

Выведем формулу, по которой разыскивается число d. Как известно, уравнение касательной к кривой y = f(x) в точке (a₀, f(a₀)) может быть записано в виде:

Подставляем сюда координаты (d, 0) точки пересечения касательной с осью х, получим:

откуда:

                                  d =  .                  (2)

Если соединить на рис. 3-6 точками А и В хордами, то обнаружится, что методы линейной интерполяции и Ньютона во всех случаях дают приближение к истинному значению с разных сторон.

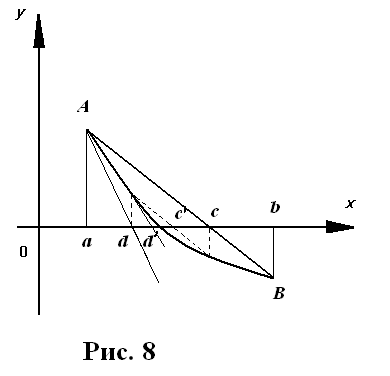
Целесообразно поэтому, если отрезок (a, b) уже такой, как это требуется в методе Ньютона, комбинировать два эти метода. Мы получим этим путем много более тесные границы c и d для корня α.

Если они ещё не дают требуемой точности приближения, то к этим пределам следует применить ещё раз указанные оба метода (см. рис. 8) и т. д., до тех пор пока не вычислим корень α с любой, наперёд заданной, точностью. [3]

Метод Лобачевского-метод приближенного нахождения корней алгебраических уравнений. Лобачевского метод состоит в следующем. Пусть требуется найти корнии x₁,x₂,…,x_n уравнения:  

С помощью указанных Лобачевским формул:

…………………….

строится многочлен: корни которого являются квадратами корней уравнения (*).

Продолжая этот процесс -квадрирование, строят многочлены f₂ (х), f₃(x) ит. д., где многочлен

 его корнями будут числа

при этом коэффициенты a_i^(k+1) многочлена f_k+1 (x) получаются возведением в квадрат коэффициентов a_i(k) многочлена f_k (x) т. е. имеет место приближенное равенство:

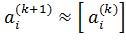 в пределах устанавливаемой точности, следовательно, и корни многочлена f(х) могут быть найдены приближенно по тем же формулам:

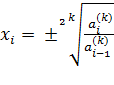. Знак корня определяется подстановкой в исходное уравнение. При этом предполагается, что корни действительны и различны и такие, что удовлетворяют условию:             

 где знак » означает «значительно больше». При выводе формулы (**) используется зависимость (обобщенная теорема Виета) между корнями и коэффициентами уравнения. Нарушение отмеченной закономерности между корнями (когда корни по значению близки или комплексные) влечет за собой нарушение указанной аналогичной закономерности между коэффициентами.

Лобачевского метод может быть использован и для приближенного вычисления комплексных корней, хотя при этом вычисления усложняются, а действительные корни находятся по приближенной формуле (**). Лобачевского метод был описан Лобачевским в его книге «Алгебра или исчисление конечных» (1834).

Лобачевского метод в литературе встречается как Греффе метод — по имени швейцарского математика К. Греффе, или Данделена метод — по имени бельгийского математика Ж. Данделена, открывших этот метод независимо от Лобачевского.

Выводы

Методы математических расчетов человек использовал с давних времен. Становление и развитие математики как науки, возникновение её новых разделов тесно связано с развитием потребностей общества в измерениях, контроле, в таких областях деятельности как промышленность, сельское хозяйство, строительство и многих других.

Понятие числа было неотделимо от культурного прогресса времени, а смысл числа всегда сопровождался и числовыми выражениями, и иллюстрациями. Математика придавала законченный вид всем наукам, где она применялась. Очень большие вычисления связаны с физикой, химией. Многие задачи вычислений связаны с уравнениями и их решением.

Первое знакомство с уравнениями происходит в школьном курсе математики уже в четвёртом классе. В дальнейшем учащиеся знакомятся со всё более сложными уравнениями.