ОБ ОСОБОМ ПОЛИТРОПНОМ ПРОЦЕССЕ С БЛИЗКИМ К ИЗОТЕРМЕ ПОКАЗАТЕЛЕМ

ABOUT A SPECIAL POLYTROPIC PROCESS WITH AN INDEX CLOSE TO ISOTHERM

Nodir Kodirov

Independent researcher, Uzbekistan

Аннотация. В статье показан гипотетический особый политропный процесс, показатель которого оказывается близким к изотерме.

Abstract. The article shows a hypothetical special polytropic process, the index of which turns out to be close to the isotherm.

Ключевые слова: прямой политропный процесс; особый политропный процесс; показатель процесса; политропа; изотерма.

Keywords: direct polytropic process; special polytropic process; process index; polytrope; isotherm.

1. Введение

Из термодинамики известно, что вся подводимая к рабочему телу теплота преобразуется в работу только в одном термодинамическом процессе идеального газа-изотермическом [2, с.84-85]. Целью настоящего исследования является выяснение ответа на вопрос о том, может ли какой-либо другой тепловой процесс быть близким к изотермическому процессу идеального газа. Далее по тексту под работой политропного процесса подразумевается работа рабочего тела, необязательно идеального газа.

2. Метод исследования

Исследование производится графическим способом, который и применил первооткрыватель политропного процесса, Автор источника [1] G.Zeuner в XIX веке, результат исследования проверяется численным расчетом.

3. Результаты исследования

3.1. Прямой политропный процесс

Политропным процессом называется такой процесс, когда теплоемкость идеального газа постоянна [2, с.89]. Графическое изображение прямого политропного процесса, выражаемого кривой a1b, приведено на рис.1 ниже.

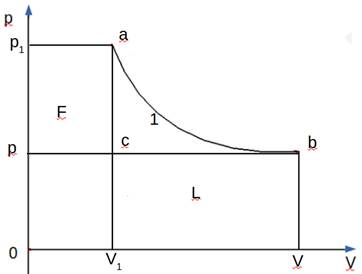
Рисунок 1. Располагаемая внешняя работа и работа изменения объёма в политропном процессе a-1-b на р-V диаграмме [1, с. 144] (дополнен точками с и 1)

Согласно описанию, площадь фигуры, ограниченной точками a-1-b-p-p₁, выражает располагаемую внешнюю работу, а площадь фигуры, ограниченной точками a-1-b-V₁-V, выражает работу изменения объёма, их отношение есть показатель этого процесса. Интересен вывод уравнения показателя процесса, поэтому цитируем первоисточник. Работа изменения объема:

 [1, с.145]                          (1)

Располагаемая внешняя работа:

[1, с.145]                          (2)

Преобразуем последнее уравнение:

= = (3)

Показатель прямого политропного процесса:

                            (4)

Другими словами, открывший политропный процесс G.Zeuner вывел уравнение показателя процесса геометрическим способом без оперирования бесконечно малыми величинами. Выведем это же уравнение несколько иначе. Площадь фигуры a1bc по работе изменения объёма:

                                 (5)

 Площадь той же фигуры a1bc по располагаемой внешней работе:

                                 (6)

Приравниваем:

Преобразуем:

=

=

и получаем уравнение (2), из которого и выводятся уравнения (3) и (4). Кроме того, по определению в политропном процессе:

[1, с.143]

Из чего и уравнения отношения объёмов V и V₁:

                                               (7)

следует:

Откуда:

                                            (8)

3.2. Особый политропный процесс

Допустим теперь, что возможно совершить особый политропный процесс, зеркально симметричный прямому, выражаемый кривой a-2-b, полученный симметричным переносом кривой a-1-b, выражающей прямой политропный процесс, относительно отрезка а-3-b, изображенной на рис.2 ниже. Из рис.2 очевидно, что параметры точек a (p₁;V₁) и b (p;V) не изменились.

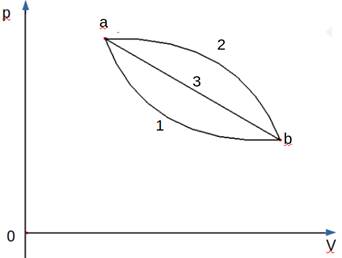
Рисунок 2.Прямой a-1-b и особый a-2-b политропные процессы на p-V диаграмме

Тогда графическое изображение прямого и особого политропных процессов и работ соответствует рис.3. ниже, согласно которому располагаемая внешняя работа особого политропного процесса равна площади фигуры, ограниченной точками р₁-a-2-b-p, которую можно выразить как разницу площадей фигур, ограниченных точками p₁-d-b-p и a-d-b-2, а работа изменения объёма того же процесса, равна площади фигуры, ограниченной точками a-2-b-V-V₁, которую можно выразить как разницу площадей фигур, ограниченных точками a-d-V-V₁ и a-d-b-2.

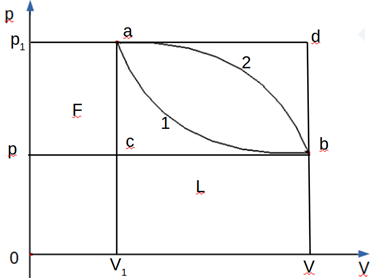
Рисунок 3. Располагаемая внешняя работа и работа изменения объёма в прямом a-1-b и особом a-2-b политропных процессах на р-V диаграмме

Теперь можно вычислить показатель особого политропного процесса. Площадь фигуры adb2 по работе изменения объёма в прямом политропном процессе:

 Площадь той же фигуры adb2 по располагаемой внешней работе в прямом политропном процессе:

Располагаемая внешняя работа в особом политропном процессе через работу изменения объёма в прямом политропном процессе:

=

==      

=

С учетом уравнений (7) и (8):

= =                         (9)

Работа изменения объёма в особом политропном процессе через располагаемую внешнюю работу в прямом политропном процессе:

=

Согласно уравнению (4), располагаемая внешняя работа F больше работы изменения объема L в n раз, поэтому далее можно не преобразовывать, а сразу записать из уравнения (9):

                    (10)

Находим показатель особого политропного процесса:

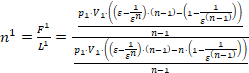=                            (11)

4.Вывод

В табл.1 ниже значения показателей особого политропного процесса, вычисленные по уравнению (11) для разных отношений объёмов и показателей прямого.

Таблица 1

Вычисленные значения показателей особого политропного процесса

Из табл.1 очевидно, что при увеличении отношения объёмов и понижении показателя прямого политропного процесса, показатель особого политропного процесса приближается к 1, то есть к показателю изотермического процесса. Другими словами, если идеальный газ расширяется по особому политропному процессу, то почти точно так же, как и в изотермическом [2, с.84-85], почти вся подводимая теплота, работа изменения объема и располагаемая внешняя работа должны быть равны между собой.

5.Заключение

Как уже сказано выше, только в изотермическом процессе идеального газа, графическое изображение которого приведено на рис.4 a) ниже, вся подводимая теплота, работа изменения объема и располагаемая внешняя работа равны между собой. Строго говоря, так как в таком процессе теплоёмкость постоянна, то изотермический процесс с равным 1 показателем является частным случаем политропного процесса [2, с.88}.

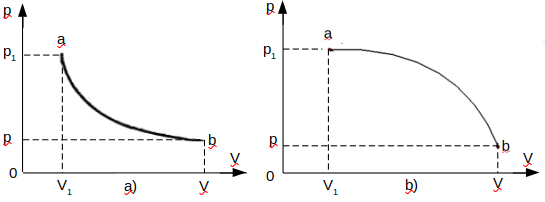
Рисунок 4. Изотермический a-b процесс a) [2, с.84] (отредактированный) и  особый политропный процесс a-b, b) на р-V диаграмме  

Другими словами, если вся подводимая теплота преобразуется в работу в изотермическом процессе, графическое изображение которого приведено на рис.4 a) выше, то теоретически почти вся подводимая теплота преобразуется в работу и в исследованном выше особом политропном процессе, графическое изображение которого приведено на рис.4 b) выше.