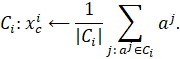КЛАСТЕРИЗАЦИЯ ЭЛЕКТРОЭНЕРГЕТИЧЕСКИХ СИСТЕМ НА ЗОНЫ НАДЕЖНОСТИ С ИСПОЛЬЗОВАНИЕМ МЕТОДА K-СРЕДНИХ НА НЕЙРОННЫХ ПРОЦЕССОРАХ

CLUSTERING OF ELECTRIC POWER SYSTEMS INTO RELIABILITY ZONES USING THE K-MEANS METHOD ON NEURAL PROCESSORS

Dmitry Krupenev

Candidate of Technical Sciences, Associate Professor, Melentyev Energy Systems Institute SB RAS, Russia, Irkutsk

Denis Boyarkin

Candidate of Technical Sciences, Melentyev Energy Systems Institute SB RAS, Russia, Irkutsk

Tatyana Gruzdeva

Candidate of Physico-Mathematical Sciences, Matrosov Institute of System Dynamics and Control Theory SB RAS, Russia, Irkutsk

Аннотация. При оценке балансовой надёжности выполняется многократное решение задачи оптимизации, а именно минимизации дефицита мощности. При этом современные энергосистемы включают в себя огромное количество элементов со своими свойствами и спецификой работы. Всё это приводит к росту размерности данных, описывающих энергосистему и вычислительным трудностям при выполнении расчётов. Для снижения размерности в энергосистемах выделяются укрупненные узлы – зоны надёжности, объединяющие в себе группы элементов. В статье для выделения зон надёжности предлагается использовать метод k-средних, реализованный на нейронном процессоре.

Abstract. When assessing adequacy, a multiple solution of the optimization problem is performed, namely, minimization of power deficit. At the same time, modern energy systems include a huge number of elements with their own properties and specifics of operation. All this leads to an increase in the dimensionality of the data describing the energy system and computational difficulties in performing calculations. To reduce the dimensionality in power systems, enlarged nodes are identified - reliability zones, combining groups of elements. In the article, the k-means method implemented on a neural processor is proposed to be used to identify reliability zones.

Ключевые слова: электроэнергетическая система; балансовая надежность; зона надежности; кластеризация; метод k-средних; NPU.

Keywords: electric power system; adequacy; reliability zone; clustering; k-means method; NPU.

Введение

Электроэнергетические системы (ЭЭС) включают в себя сотни тысяч разнородных элементов, работающих в общем режиме работы [14], в числе которых блоки генерации, электростанции, линии электропередачи, трансформаторы, установки потребления и др. Для стабильной работы ЭЭС как системы регулярно проводятся мероприятия по поддержанию и повышению её надёжности. Для обоснования таких мероприятий выполняются различные аналитические расчёты, в том числе оценка балансовой надёжности [1,6,9]. Для этого, как правило, используется методика, основанная на методе Монте-Карло [10], которая является наиболее вычислительно эффективной по сравнению с другими используемыми методами [4]. Размерность современных ЭЭС, разнообразие свойств её элементов делают анализ балансовой надёжности вычислительно сложным даже при использовании метода Монте-Карло. В таком случае прибегают к снижению размерности исходной задачи, например, к укрупнению структуры рассматриваемой ЭЭС (кластеризации). Для этого ЭЭС разделяется на зоны надёжности (ЗН), включающие в себя различные группы элементов системы, формируются энергетические расчетные модели (ЭРМ), при этом внутри ЗН исключаются сетевые ограничения.

Формирование ЭРМ выполняется, как правило, до проведения расчётов и принимается как новая структура ЭЭС, которая остается неизменной для всего периода, для которого выполняется оценка балансовой надёжности. В этом случае наиболее широко используемым способом определение границ ЗН является экспертный, наиболее существенными недостатками которого являются временные затраты. Однако, может возникать необходимость многократной кластеризации в цикле оценки балансовой надежности. Такое требование возникает при существенном изменении параметров ЭЭС в течении расчетного периода и, соответственно, влиянии этих параметров на возможности сети по передачи мощности. Также это может быть обусловлено тем, что современные ЭЭС имеют сложную структуру с большим разнообразием энергетического оборудования. В таких случаях применение экспертного подхода невозможно, возникает необходимость применения быстрых методов кластеризации, способных уточнять структуру ЭРМ при оценке балансовой надёжности, не оказывая существенного влияния на совокупное время выполнения расчётов. В практике решения задач анализа систем разработаны различные методы кластеризации [2,7], но для оценки балансовой надежности формализованных методик кластеризации не существует. В статье предлагается использование одного их самых простых, но эффективных методов кластеризации – метода k-средних, ускоренного за счёт адаптации к работе на тензорных процессорах. 

Постановка задачи кластеризации ЭЭС

Для максимально быстрого и точного решения задачи кластеризации ЭЭС на ЗН и формирования ЭРМ необходимо разработать подход, который будет максимально полно отражать влияющие критерии и ограничения на уровень БН ЭЭС и позволит достаточно быстро и адаптивно проводить кластеризацию ЭЭС в процессе проведения исследований.

При формировании алгоритма кластеризации ЭЭС на зоны надежности необходимо получить функцию , которая каждый узел ЭЭС () включает в зону надежности . В рассматриваемом случае множество , т.е. количество зон надежности, неопределенно. Оптимальное число зон надежности необходимо определить в процессе вычислений.  Стоит отметить, что, как и в любом примере кластеризации, для решаемой задачи справедлива теорема невозможности Клейнберга, в которой указывается, что не существует оптимального алгоритма кластеризации. Каждый применяемый алгоритм будет вносить свою специфику в конечное решение. Это будет зависеть от выбранного критерия и метрики кластеризации.

Решением задачи кластеризации ЭЭС будет являться ее деление, удовлетворяющее заданному критерию оптимальности. В рассматриваемом случае критерием оптимальности выступает минимизация числа зон надежности:

Стремление к минимуму числа зон надежности является естественным, так как это в дальнейшем анализе балансовой надежности приведет к снижению размерности ЭРМ.

Ограничением при решении поставленной задачи будет выступать ограничение, заданное на метрику, которая формируется из различных признаков. В рассматриваемом случае метрика кластеризации должна включать как технические, так и экономические признаки. К техническим признакам можно отнести: установленную мощность генерирующего оборудования в узлах ЭЭС; среднее значение числа часов использования установленной мощности в узлах ЭЭС; сезонные максимумы и минимумы потребления мощности в узлах ЭЭС; аварийность энергетического оборудования; нормативы на проведение плановых ремонтов энергетического оборудования; длины линий электропередачи(ЛЭП) между узлами ЭЭС; пропускные способности ЛЭП [15]. К экономическим: стоимость ввода генерирующих и сетевых объектов. От выбора метрики в итоге будет зависеть результат кластеризации. Метрика должна максимально отражать специфику работы ЭЭС и влияние учитываемых признаков на кластеризацию.

Кластеризация методом k-средних

В настоящее время разработано достаточно большое количество алгоритмов кластеризации в наборах данных [3,5,8,12], каждый из которых обладает своей спецификой, имеет свои достоинства и недостатки. Метод k-средних (k-means) [5] – это один из наиболее популярных методов кластеризации, принадлежащий к классу методов разбиения. Он основан на разделении вершин графа на заданное число кластеров, так чтобы минимизировать сумму квадратов расстояний между вершинами и центрами кластеров.

Алгоритм k-means состоит из двух основных шагов: назначение элементов данных текущим ближайшим (по квадрату евклидова расстояния) центрам кластеров с последующим пересчетом центров как средних значений элементов данных, назначенных тем же кластерам. Алгоритм завершается, когда нет никаких изменений в назначениях кластеров достаточно большого количества элементов данных:

1. Выбираются начальные центры кластеров  Выбор начальных центров кластеров производится случайным образом, например из числа элементов данных, или по определенному алгоритму.

2. До тех пор, пока кластеры  изменяются, то есть изменяются координаты их центров , выполняются следующие шаги:

2.1. Для каждой точки набора данных , определяется ближайший центр кластера по формуле квадрата евклидова расстояния (2). Таким образом формируются кластеры , состоящие из элементов данных, ближайших к центру .

где m – количество элементов в наборе данных.

2.2. Для каждого кластера вычисляется новый центр как среднее значение соответствующих координат всех точек, относящихся к данному кластеру (центр масс) по формуле (3):

Наиболее трудоемкими операциями в данном алгоритме являются поиск ближайшего центра кластера и пересчет координат центров кластеров. Поскольку они могут выполняться одновременно для каждого элемента данных (кластера), часто применяются процедуры распараллеливания с общей памятью для ускорения работы алгоритма (SMA). Это делает перспективным использование таких процессоров, которые позволяют эффективно выполнять параллельные вычисления, например GPU или NPU.

Нейронные процессоры (NPU) — это узкоспециализированные процессоры, разработанные специально для выполнения задач искусственного интеллекта (ИИ). Они оптимизированы для выполнения сложных и ресурсоемких математических вычислений, необходимых в алгоритмах машинного обучения и искусственных нейронных сетях. Наиболее интересными в контексте задачи являются тензорные процессоры. Такие процессоры работают с тензорами — объектами, которые могут быть представлены как многомерные массивы чисел. Тензорные процессоры специализированы для быстрого выполнения таких операций, как матричное умножение и свёртка, используемых для эмуляции свёрточных нейронных сетей, однако, они подходят для любых алгоритмов, которые могут быть представлены в виде операций с матрицами.

Как сказано выше, в этой статье мы предлагаем использовать реализацию NPU-ускоренного алгоритма k-means, в котором наиболее трудоемкие операции вычисления расстояний и пересчет центров кластеров представлены в виде матриц (говоря в контексте NPU, в виде тензоров) и операций над ними, которые выполняются очень эффективно на нейронных процессорах.

Экспериментальные исследования

Для оценки работы алгоритма k-means, ускоренного NPUбыли выполнены экспериментальные исследования на тестовой схеме Объединенной энергосистемы (ОЭС) Сибири, которая включает в себя Алтайскую, Бурятскую, Иркутскую, Красноярскую, Кузбасскую, Новосибирскую, Омскую, Томскую, Хакасскую и Забайкальскую энергосистемы. Схема была представлена в виде неориентированного графа, в котором каждая из вершин характеризуется генерацией и нагрузкой, а ребра – линии, характеризуются длиной и напряжением. Таким образом задача сводится к кластеризации на графах.  Исходные данные ОЭС Сибири были приняты в соответствии [13], полученный граф по схеме ОЭС Сибири состоит из 540 генерирующих и нагрузочных узлов (вершин) и 1025 линий электропередачи (рёбер).

На рисунке1показан результат работы алгоритма в виде графического представления разделения узлов ОЭС Сибири по зонам надежности (кластерам).

Рисунок 1. Графическое представление отнесения узлов ОЭС Сибири к зонам надежности на основании применения алгоритма k-means

Та же кластеризация, но уже в границах географических регионов представлена на рисунке 2.

Рисунок 2. Результат кластеризации ОЭС Сибири на ЗН на основании применения алгоритма k-means (географическое представление)

В результате выполнения кластеризации методом k-means было получено 14 зон надежности. Время, затраченное на кластеризацию, составило всего 0.05 с., для сравнения в предыдущей работе, где мы использовали алгоритм Лейдена [11], скорость кластеризации составила 1.16 с. Полученный результат является достаточным не только для проведения кластеризации ЭЭС перед проведением оценки балансовой надёжности, но и при необходимости изменения структуры системы в процессе расчёта без существенного изменения времени общего расчёта.

Что касается качества кластеризации, анализ полученных зон надёжности показывает, что алгоритм выполнил кластеризацию по наиболее узким местам ЭЭС с точки зрения плотности взаимосвязей и их пропускной способности, то есть полученное разбиение соответствует реальной обстановке. Полученные зоны надежности получились максимально независимыми с наименьшим количеством связей между друг другом. Такое деление при последующей оценке балансовой надежности будет хорошо определять загруженность связей и объектов энергетической инфраструктуры.

Заключение

В представленном исследовании рассмотрена задача формирования энергетических расчетных моделей, которые используются при оценке балансовой надежности электроэнергетических систем. Был проведен анализ методов кластеризации, и определено, что одним из наиболее подходящих способов кластеризации ЭЭС на зоны надежности является метод k-средних (k-means).

На рисунке 2 видно, что при формировании зон надежности были учтены все основные ограничения на передачу мощности в ОЭС Сибири. Границы сформированных зон надежности коррелируют с соответствующими контролируемыми сечениями в электрической сети, несмотря на то что информация о контролируемых сечениях явно не использовалась в рамках примененного подхода. Это говорит об адекватности полученного результата. Также применение метода k-means позволило существенно ускорить этап разбиения ЭЭС на ЗН, позволяя широко использовать процедуру кластеризации, включая её многократное выполнение в процессе расчёта, ранее это было невозможно.

Таким образом, можно заключить, что использование метода k-means позволяет формализовать определение зон надежности непосредственно в рамках выполнения расчетов, что способствует повышению эффективности решения задач анализа и синтеза балансовой надежности.

Источники финансирования

Исследование выполнено за счет гранта Российского научного фонда № 23-71-01090.