Алгоритм непараметрической оценки регрессии с адаптивной шириной окна
Конференция: VII Международная научно-практическая конференция "Научный форум: технические и физико-математические науки"
Секция: Информатика, вычислительная техника и управление

VII Международная научно-практическая конференция "Научный форум: технические и физико-математические науки"
Алгоритм непараметрической оценки регрессии с адаптивной шириной окна
Nonparametric regression estimation algorithm with adaptive bandwidth
Bugaenko Aleksandr
master, Siberian State University of Science and Technologies, Russia, Krasnoyarsk
Milov Anton
Master, Siberian State University of Science and Technologies, Russia, Krasnoyarsk
Аннотация. В данной работе предлагается подход к нахождению переменной ширины окна при построении непараметрических моделей на основе оценки Надарая-Ватсона. Данный подход позволяет решать ряд задач, связанных с моделированием зависимостей, со временем меняющих свой характер.
Annotation. In this paper we propose an approach for finding the variable bandwidth when constructing nonparametric models based on the Nadaraya-Watson kernel regression estimate. This approach allows us to solve a number of problems related to the modeling of dependencies that change their character over time.
Ключевые слова: ядерное сглаживание; адаптивная ширина окна.
Ключевые слова: kernel regression; adaptive bandwidth.
Непараметрические модели на основе оценки Надарая-Ватсона (1964 г.) широко используются в задачах регрессии, сглаживания данных, поиска выбросов и многих других. Их использование эффективно в тех случаях, когда затруднен выбор подходящей параметрической модели из-за отсутствия априорных знаний о моделируемом явлении. В случае непараметрического моделирования выходной величины, меняющей характер зависимости, возникает трудность настройки параметра размытости, например, в случае моделирования периодических процессов с переменной частотой и (или) амплитудой.
Одним из подходов, позволяющих справиться с данной проблемой, является использование ансамблей непараметрических моделей. Ансамблем называется несколько моделей одного или разных типов, составленных по очереди. Причем, каждая из последующих моделей, добавляемых в ансамбль, аппроксимирует ошибку ансамбля на предыдущей итерации. Подробно данный подход применительно к непараметрическим моделям отражен в [5].
Другой подход подразумевает использование окна переменной ширины, выбираемой таким образом, чтобы в окрестности каждой точки искомая зависимость восстанавливалась наилучшим образом. В литературе данный подход встречается при решении проблем, возникающих в случае работы с разреженными данными [3]. Он заключается в подборе ширины окна таким образом, чтобы в областях с разреженными точками в окно при построении модели попадало не меньше заданного числа точек. Однако такой подход никак не учитывает возможные изменения в характере моделируемой зависимости.
В данной работе предлагается алгоритм построения непараметрических моделей с адаптивной шириной окна для восстановления неизвестных зависимостей, существенно меняющих свой характер на разных интервалах области определения функции.
Постановка задачи.
Пусть задано пространство объектов X и множество возможных ответов Y Ì R. Существует неизвестная зависимость ![]() , значения которой известны только на объектах обучающей выборки. Кроме того, к этим значениям добавляется нормально распределенный шум с нулевым математическим ожиданием и конечной дисперсией. Таким образом получаем выборку
, значения которой известны только на объектах обучающей выборки. Кроме того, к этим значениям добавляется нормально распределенный шум с нулевым математическим ожиданием и конечной дисперсией. Таким образом получаем выборку ![]() . Требуется построить модель
. Требуется построить модель ![]() , аппроксимирующую неизвестную зависимость
, аппроксимирующую неизвестную зависимость ![]() (х).
(х).
При отсутствии знания о структуре уравнения для восстановления зависимости используется непараметрическая оценка регрессии Надарая-Ватсона [2]. Стоит отметить, что указанная в (1) формула обобщает одномерные и многомерные задачи, т.к. ![]() может быть как скалярной величиной, так и вектором.
может быть как скалярной величиной, так и вектором.
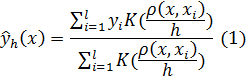
Значение функции ядра ![]() в точке характеризует ее вес при оценке значения восстанавливаемой функции. Функция ядра должна удовлетворять известным условиям сходимости оценок [4] быть четной, гладкой и ограниченной. Таким образом, чем дальше расположена точка обучающей выборки от точки, в которой восстанавливается значение функции, тем меньший вес она будет иметь.
в точке характеризует ее вес при оценке значения восстанавливаемой функции. Функция ядра должна удовлетворять известным условиям сходимости оценок [4] быть четной, гладкой и ограниченной. Таким образом, чем дальше расположена точка обучающей выборки от точки, в которой восстанавливается значение функции, тем меньший вес она будет иметь.
Параметр h называется шириной окна сглаживания. Выбор ширины окна оказывает основное влияние на качество восстановления зависимости. При слишком узком окне функция ![]() стремится пройти через все точки обучающей выборки, что делает оценку чувствительной к помехам измерения. При слишком большом значении h функция становится излишне сглаженной и слабо отражает характер исходной зависимости.
стремится пройти через все точки обучающей выборки, что делает оценку чувствительной к помехам измерения. При слишком большом значении h функция становится излишне сглаженной и слабо отражает характер исходной зависимости.
Проблема данного подхода заключается в том, что подобная оценка в некоторых случаях не способна должным образом аппроксимировать искомую зависимость, например, когда зависимость имеет периодический характер с переменной частотой и амплитудой. На рисунке 1 представлен пример подобной ситуации.
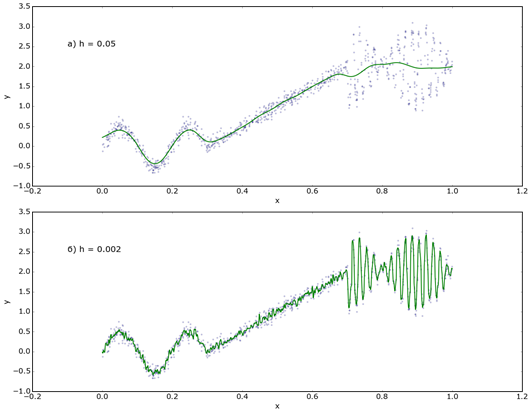
Рисунок 1. Проблемы при аппроксимации значений функции с помощью непараметрической модели с постоянной шириной окна
Для демонстрации описываемого эффекта была взята функциональная зависимость следующего вида:
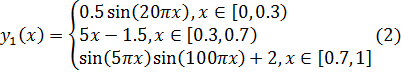
Было сгенерировано 2000 точек, равномерно распределенных на отрезке [0, 1], рассчитано значение функции ![]() в них и добавлена аддитивная помеха, сгенерированная из стандартного нормального распределения
в них и добавлена аддитивная помеха, сгенерированная из стандартного нормального распределения ![]() . Эти точки использовались для построения непараметрической модели с постоянной шириной окна.
. Эти точки использовались для построения непараметрической модели с постоянной шириной окна.
Ширина окна, при которой зависимость хорошо аппроксимируется на интервале (0, 0.7) (рис. 1а), не позволяет восстановить высокочастотные изменения функции на интервале (0.7, 1), и наоборот, ширина окна, являющаяся оптимальной для второго интервала, приводит к переобучению на первом (рис. 1б).
Данную проблему предлагается решить с помощью адаптивной ширины окна, которая находится из описанных ниже соображений.
Алгоритм AdaWind.
Оценка регрессии с использованием адаптивной ширины окна строится в предположении функциональной зависимости ширины окна от значения входной переменной и имеет следующий вид:
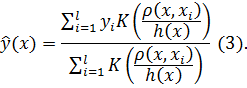
Необходимо найти такую функцию ![]() , которая обеспечивала бы хорошее качество аппроксимации во всех точках обучающей выборки. Для нахождения данной функции использовалась следующая эвристика.
, которая обеспечивала бы хорошее качество аппроксимации во всех точках обучающей выборки. Для нахождения данной функции использовалась следующая эвристика.
Первоначально генерируется множество значений параметра ширины окна ![]() , например, по формуле
, например, по формуле ![]() , j – показатель степени. Основная идея заключается в том, что данное множество должно обеспечивать достаточное разнообразие значений. Иными словами, в нем должны присутствовать такие значения параметра, которые позволяют построить модель с хорошим качеством аппроксимации на каком-либо фрагменте обучающей выборки. Чем больше изменений характера зависимости претерпевает исходная функция, тем лучше должен быть охват значений параметра ширины окна множеством H. В таком случае имеет смысл брать значение параметра
, j – показатель степени. Основная идея заключается в том, что данное множество должно обеспечивать достаточное разнообразие значений. Иными словами, в нем должны присутствовать такие значения параметра, которые позволяют построить модель с хорошим качеством аппроксимации на каком-либо фрагменте обучающей выборки. Чем больше изменений характера зависимости претерпевает исходная функция, тем лучше должен быть охват значений параметра ширины окна множеством H. В таком случае имеет смысл брать значение параметра ![]() близким к единице. Значения
близким к единице. Значения ![]() не должны быть меньше минимальной ширины окна, при которой в любой точке определения функции в окно попадает хотя бы одна точка обучающей выборки. Значение
не должны быть меньше минимальной ширины окна, при которой в любой точке определения функции в окно попадает хотя бы одна точка обучающей выборки. Значение ![]() рекомендуется брать достаточно большим, при котором происходит чрезмерное сглаживание.
рекомендуется брать достаточно большим, при котором происходит чрезмерное сглаживание.
После этого строятся непараметрические модели с различной шириной окна ![]() . В каждой точке
. В каждой точке ![]() выбираем такое
выбираем такое ![]() при котором в ɛ-окрестности этой точки (множество
при котором в ɛ-окрестности этой точки (множество ![]() ) непараметрическая модель даёт наименьший средний модуль ошибки (6). Для вычисления среднего модуля ошибки можно воспользоваться непараметрической моделью с прямоугольным ядром и шириной окна равной ɛ (4, 5).
) непараметрическая модель даёт наименьший средний модуль ошибки (6). Для вычисления среднего модуля ошибки можно воспользоваться непараметрической моделью с прямоугольным ядром и шириной окна равной ɛ (4, 5).
В случае выбора малого значения ![]() ширина окна будет сильно зашумлена, что скажется на итоговой модели. Выбор больших значений приводит к тому, что на участках, где характер исходной зависимости меняется, значения функции ширины окна меняются слишком медленно. В качестве значения параметра ɛ можно взять оптимальное по среднеквадратичному критерию ошибки значение ширины окна h при использовании непараметрической модели с постоянной шириной окна.
ширина окна будет сильно зашумлена, что скажется на итоговой модели. Выбор больших значений приводит к тому, что на участках, где характер исходной зависимости меняется, значения функции ширины окна меняются слишком медленно. В качестве значения параметра ɛ можно взять оптимальное по среднеквадратичному критерию ошибки значение ширины окна h при использовании непараметрической модели с постоянной шириной окна.
На рисунке 2 изображен график значений усредненного по ɛ-окрестности модуля ошибки для различных значений ширины окна ![]() .
.
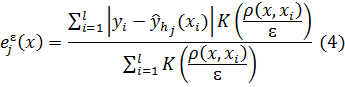
![]()
![]()
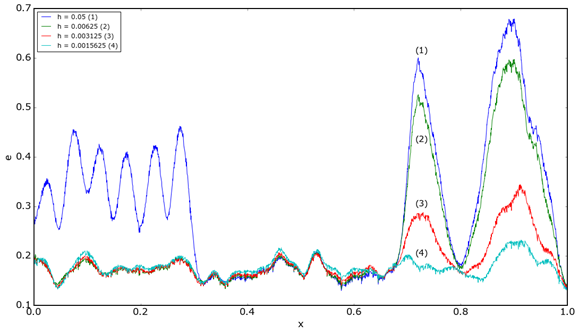
Рисунок 2. График значений усредненного по ɛ-окрестности модуля ошибки для различных значений ширины окна (ɛ = 0.005)
В завершение строится модель регрессии ![]() по имеющимся точкам
по имеющимся точкам ![]()
В данной работе предлагается восстановление функции ![]() c помощью деревьев регрессии. Этот алгоритм позволяет представить функцию
c помощью деревьев регрессии. Этот алгоритм позволяет представить функцию ![]() в виде кусочно-ступенчатой функции. На рисунке 3 отображены выбранные в точках обучающей выборки значения ширины окна
в виде кусочно-ступенчатой функции. На рисунке 3 отображены выбранные в точках обучающей выборки значения ширины окна ![]() и построенная на их основании модель
и построенная на их основании модель![]()
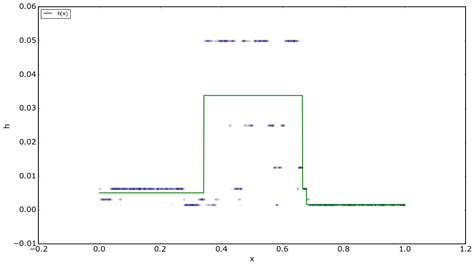
Рисунок 3. Значения ![]() и построенная по ним модель
и построенная по ним модель ![]()
Алгоритм построения деревьев регрессии для построения функции ширины окна был выбран по причине того, что он позволяет наглядно выделять интервалы, на которых характер зависимости разнится. Подробное описание данного алгоритма содержится в [1].
При восстановлении значения в новой точке ![]() , сначала находится значение предпочтительной ширины окна в этой точке
, сначала находится значение предпочтительной ширины окна в этой точке ![]() и затем вычисляется оценка регрессии по формуле (3).
и затем вычисляется оценка регрессии по формуле (3).
Результаты.
Для тестирования алгоритма использовалась описанная задача восстановления регрессии. Уравнение исходной зависимости представлено в (2).
Относительная ошибка аппроксимации (7) составила с помощью модели с постоянной шириной окна составила 0.11, при использовании алгоритма AdaWind эта величина составила 0.09.
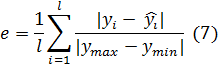
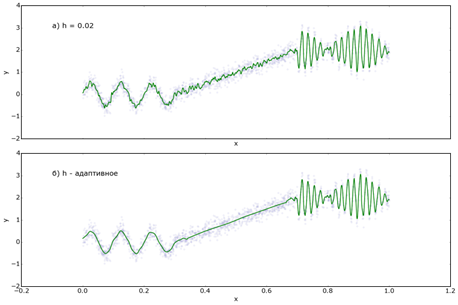
Рисунок 4. Восстановление зависимости ![]() c использованием непараметрической модели с постоянной шириной окна (а) и алгоритма AdaWind (б)
c использованием непараметрической модели с постоянной шириной окна (а) и алгоритма AdaWind (б)

