О предполагаемом методе Ферма

ABOUT THE PROPOSED FERMAT’S METHOD

Vyacheslav Chursin

 candidate of physico-mathematical sciences, assistant professor, Russia, Orsk

Аннотация. В статье рассматривается доказательство теоремы Ферма для случаев n=3,5. Целью публикации является показать, что П. Ферма скорее всего обладал методом элементарного доказательства неразрешимости уравнения  в ненулевых целых числах. Помимо доказательства теоремы Ферма в публикации рассматриваются новые классы так называемых псевдочетных чисел.

Abstract. The article discusses the proof of Fermat's theorem for the cases n=3, 5. The purpose of the publication is to show that P. Fermat probably possessed the elementary method of proof of the unsolvability of the equation in nonzero integers. In addition to the proof of Fermat's theorem in the publication describes the new classes of the so-called pseudogenic numbers.

Ключевые слова: Последняя теорема Ферма, метод элементарного доказательства теоремы Ферма для случаев n=3,5.

Keywords: Fermat's last theorem, the method of the elementary proof of Fermat's theorem for the cases n=3,5.

История доказательства Последней теоремы Ферма – это уникальная история математической проблемы, волнующая умы профессиональных математиков и любителей математики на протяжении почти трехсот с лишним лет. Доказательство теоремы, представленное Эндрю Джон Уайлсомв 1995 г., не сняло другого вопроса –  обладал ли П.Ферма элементарными методами доказательства этой теоремы? Сложность доказательства теоремы, предложенного Э. Уайлсом, заставило сомневаться некоторых математиков всамойвозможности доказательства данной проблемы П.Ферма при помощи тех элементарных методов, которые были в его распоряжении. В представленной статье попытаемся дать положительный ответ на поставленный вопрос и показать (пусть хотя бы и для частных случаев), что существуют элементарные методы, при помощи которых можно доказать данную теорему.

Прежде чем переходить к анализу предлагаемых методов, обратимся к знаменитым комментариям, которые дал сам П.Ферма по данной проблеме:

«Невозможно разложить куб на два куба, биквадрат – на два биквадрата и, в общем случае, любую степень, большую двух, в сумму таких же степеней; я нашел поистине чудесное доказательство, но эти поля слишком узки, чтобы его поместить» [1; с.13].

Исходя из данного комментария, большинствопозднейших предложенных методов решения поставленной теоремытрактовались следующим образом:

«Для произвольного натурального n>2 уравнение вида:

                                                                                                       (1)

не имеет решения в целых числах, каждое из которых отлично от 0». Таким образом, если следовать данной трактовке проблемы, то необходимо найти такие целые x,y и z, которые удовлетворяли бы уравнению (1).

В представленной публикации (в соответствии с комментарием П.Ферма) предлагается сместить акценты и трактовать формулировку задачи в следующем виде:

«Для произвольного натурального n>2, при ,для уравнение вида:

                                                           (2)

невозможно представить  в виде n–ой степеникакого-либо целого числа».Очевидно, что при такой формулировке любые целые являются решением уравнения (2).И тогдаперед нами стоит только один вопрос: является ли первыйодночлен уравнения (2)n–ой степеньюкакого-либо целого числа или нет?

Дальнейшие рассуждения относительно доказательства теоремы Ферма основываются на представлении в виде уравнения (2), а так же некоторых определений и теорем (которые здесь не доказываются и являются предметом рассмотрения последующих публикаций).

Определение 1. Пусть p–простое натуральное число. Тогда однородный симметрический многочлен вида:

                                                                                       (3)

будем называть псевдочетной по p функцией, определенной на множестве целых чисел.

В ходе дальнейшихрассуждений будем использовать альтернативное представление псевдочетных по pфункций, определенных на множестве натуральных чисел и имеющих вид:

и

Определение 2.Функциювида(x±y), x, yÎN, будем называть сопряженной с функциейи наоборот – функцию будем называть сопряженной с функцией (x±y).

Основным свойством псевдочетныхпо pфункций является:

Лемма 1.  Псевдочетная по p функция обладает следующим свойством:

Следует так же отметить и обратное свойство псевдочетных по p функций, а именно то, что из того, что  следует, что
, и из того, что  следует, что
.

Лемма 2. Пусть p– простое натуральное число,  – система наименьших неотрицательных вычетов по модулю p. Тогда справедлива следующая формула:

                                                                                                     (4)

Теорема 1. Если p–простое натуральное число, то для всех m=0,1,..,p–1справедливо, что

                                                                                                       (5)

Исходя из вышеизложенной трактовки проблемы, попытаемся оценить эффективность предложенного метода и начнем рассмотрение с уравнения вида .

При поиске решения уравнения  будем исходить из следующих условий:

1)   

2)    x, y и z – взаимнопростые натуральные числа;

3)      изначально и  не предполагаются взаимнопростыми натуральными числами и имеют вид:

                                                                                                     (6)

где m и n– взаимнопростые натуральные числа.

Для решения системы (6) возведем оба уравнения системы в квадрат и вычтем из первого уравнения системы второе уравнение системы. Получим, что 4yz=q²(m²–n²)(m²+n²). Учитывая требование, что x, yиz – взаимнопростые натуральные числа, получаем, что q²=4 или q=2. Учитывая, что y<z, получим известную формулу [2; с.20]: . Из полученного решения можно вывести все хорошо известные свойства уравнения и переменных x, yиz. Хотелось бы при этом отметить следующее:

– как видно из применяемого метода, вопрос о разрешимости уравнения  свелся к вопросу о разрешимости в целых числах системы линейных уравненийc четными свободными членами, имеющими особое представление;

– одночлен  представляет собой произведение не взаимно простых сомножителей. В частности, если , то получим, что

Перейдем к рассмотрению уравнения вида:

                                                                                                   (7)

где x, y и zÎN.

Лемма 3. Если справедливо уравнение (7), то из того, что  следует, что или .

Доказательство. Преобразуем левую часть уравнения (7) к виду:
. Так как , тоимеем, что и  (согласно лемме 1). Преобразуем функцию  к виду: (здесь неявно используется теорема 1). В результате раскрытия скобок в уравнении (7), получим уравнение вида: . С учетом того, что  следует, что и , что возможно, только если  или .

Лемма 4. Если справедливо уравнение (7), то из того, что  следует, что  или .

Доказательство. Преобразуем уравнение (7) к виду:
. Так как , то  и  (согласно лемме 1). Преобразуем функцию  к виду:  (здесь неявно используется теорема 1). В результате раскрытия скобок в уравнении (7), получим уравнение вида: . С учетом того, что  следует, что и , что возможно, только если  или .

Лемма 5. Если справедливо уравнение (7), то из того, что  следует, что  или .

Доказательство. Так как переменные  входят симметрично в уравнении (7), то отсюда следует справедливость леммы 5.

Теперь уточним требования к решению уравнения (7), а именно: если требуется найти решение уравнения (7), то переменные x, yиzдолжны быть взаимнопростыми натуральными числами. Исходя из данного требования и учитывая леммы 3-5, получаем справедливость следующей теоремы 2.

Теорема 2. Если существуют решения уравнения (7), то справедливо, что произведение  не делится на 3.

Теорема 3. Не существует решения уравнения (7) на множестве N.

Доказательство. При доказательстве теоремы 3 будем исходить из метода отпротивного и предполагать, что существуют решения уравнения (7), которые удовлетворяют следующим условиям:

1)   

2)     не делится на 3;

3)    x, y и z – взаимнопростые натуральные числа;

4)      изначально  и  не предполагаются взаимнопростыми натуральными числами.

Как уже отмечалось ранее, при заданных условиях 1)-4) уравнение (7) является алгебраическим тождеством и остается только выяснить выполнимость условия 1). Для этого, прежде всего, выясним, какими свойствами обладают переменные .

Пусть

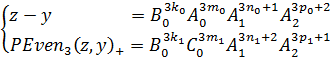
где и  – взаимнопростые числа.

Очевидно, что при таком представлении выполняется условие 1). Найдем . Тогда с учетом формулы (4) леммы 2, получим:, где . Вычитая  из второго уравнения системы, получим (с учетом теоремы 1):

,                                                                    (8)

где, ,  –функция, которая возвращает минимальное значение для значений k₁иk₂.

Очевидно, что не могут делиться на 3, так как это означало бы, что , что противоречит условию 2). Если ни одно из значений  не делится на 3, то это означает, что , так как в противном случае это означало бы, что x, yиz не взаимнопростые натуральные числа, что противоречит условию 3) (таким образом, получаем, что  и –взаимнопростые натуральные числа). С учетом вышеизложенного, формула (8) принимает вид: . В полученной формуле левая часть равенства делится на 3, в то время как правая часть делится на 3² (согласно лемме 1), что означает, что или , или , что противоречит условию 2). Таким образом, приходим к противоречию, которое и означает, что теорема 3 верна.

Рассмотрим уравнение вида:

                                                                                                     (9)  

где x, y и zÎN.

Лемма 6. Если  и не делится на 5, то .

Доказательство. Из условия  согласно лемме 1 следует, что . Тогда . Тогда учитывая, что
, а так же то, что  не делится на 5, 2 и 5 – взаимно простые числа, получаем утверждение леммы 6.

Лемма 7. Если справедливо уравнение (9), то из того, что  следует, что  или .

Доказательство. Преобразуем левую часть уравнения (9) к виду
. Так как , то имеем, что  и  (согласно лемме 1). Преобразуем функцию  к виду:  (здесь неявно используется теорема 1).В результате раскрытия скобок в уравнении (9), получим уравнение вида:. Так как , то из этого с необходимостью следует, что так же делится на , на  и так далее. Однако, из делимости на  выражения  не следует делимость на  выражения , когда  не делится на 5. Следовательно, для делимости на выражения  необходимо, что бы  или , из чего и следует справедливость леммы 7.

Аналогичным способом доказываются леммы 8 и 9.

Лемма 8. Если справедливо уравнение (9), то из того, что  следует, что  или .

Лемма 9. Если справедливо уравнение (9), то из того, что  следует, что  или .

Поиск решения уравнения (9) будем осуществлять при условии, что x, yиz являются взаимно простыми натуральными числами. Тогда с учетом вышеуказанного условия и лемм 7-9 справедлива следующая теоремы 4.

Теорема 4. Если существуют решения уравнения (9), то справедливо, что произведение  не делится на 5.

Теорема 5. Не существует решения уравнения (9) на множестве N.

Доказательство. При доказательстве теоремы 5 будем исходить из метода от противного и предполагать, что существуют решения уравнения (9), которые удовлетворяют следующим условиям:

1)   

2)     не делится на 5;

3)    x, y и z – взаимно простые натуральные числа;

4) изначально  и  не предполагаются взаимнопростыми натуральными числами и представляются следующим образом:

где и  – взаимнопростые числа.

Очевидно, что при таком представлении выполняется условие 1). Найдем . Тогда с учетом формулы (4) леммы 2, получим:. Вычитая  из второго уравнения системы, получим (с учетом теоремы 1):

,                                                    (10)

где, .

Очевидно, что не могут делиться на 5, так как это означало бы, что , что противоречит условию 2). Следовательно, только  или  делятся на 5. Однако, согласно лемме 1,  и  делятся на 5 одновременно. Таким образом, правая часть формулы (10) делится на 5², а левая делится на 5. С учетом условия 2) получаем, что  должно делиться на 5. Преобразуем  к виду:

Для первого уравнения справедливо, что из делимости  на 5 и неделимости на 5 произведения  следует, что  не делится на 5. То же самое можно утверждать и длявторого уравнения, из чего следует, что  так же не делится на 5. Но тогда, согласно лемме 6,  делится на 5, что неизбежно приводит к тому, чтоили , или , что противоречит условию 2). Таким образом, приходим к противоречию, которое и означает, что теорема 5 верна.

Выводы:

Проведенный анализ поиска решений уравнения Ферма для случаев n=3, 5 показывает:

– что существует возможность доказательства теоремы Ферма (n=3, 5) с использованием в совокупности элементарных методов и формализма псевдочетных функций;

– если удастся доказать, что , то доказательство теоремы Ферма в общем случае будет представлять собой скорее техническую, чем методологическую сложность;

– автор считает, что формализм псевдочетных функций следует рассматривать не только как инструмент классической теории чисел, но и как механизм порождения новых псевдочетных арифметик.

Список литературы:

1.  Рибенбойм П. Последняя теорема Ферма для любителей: Пер. с англ. – М.: Мир, 2003. – 429 с.

2.  Эдвардс Г. Последняя теорема Ферма. Генетическое введение в алгебраическую теорию чисел: Пер. с англ. – М.: Мир, 1980. – 477 с.