Программный алгоритм составления перестановок, размещений и сочетаний

The software algorithm of compiling permutations, placements and combinations

Ilvira Zibirova

Candidate of pedagogical Sciences, senior lecturer North Ossetian state University. K. L. Khetagurova, Russia, Vladikavkaz

Аннотация. В статье приведен компьютерный алгоритм авто­матического формирования перестановок, размещений и сочетаний элементов исходного набора.

Abstract. The paper presents a computer algorithm for automatic formation of permutations, placements and combinations of elements of the original set.

Ключевые слова: алгоритм; формирование размещений; формирование сочетаний; формирование перестановок.

Keywords: algorithm; the formation of placements; the formation of combinations; generation of permutations.

Формулы расчета количества перестановок, размещений и сочетаний изучаются в начальных курсах комбинаторики и теории вероятностей. Существует класс задач, которые решаются с их помощью. В большинстве случаев их решение основано на расчете лишь общего количества возможных комбинаций и не рассматривает качественных показателей отдельных комбинаций. Это связано с тем, что ручной подбор является долгим и трудоемким процессом. Например, дано 6 букв русского алфавита. Сколько слов, состоящих из 5 знаков, можно составить из этого набора? По формуле количества размещений несложно рассчитать, что всего можно составить 720 комбинаций. Но сколько из них будет слов? В данной статье приводится компью­терный алгоритм, позволяющий автоматически формировать комбинации перестановок, размещений и сочетаний элементов исходного набора.

Важно отметить, что в специализированной литературе, в частности [1], есть примеры алгоритмов подобного назначения, но наш вариант коренным образом отличается от них большей простотой, скоростью работы, надежностью и использованием рекурсии. Алгоритм представлен в виде готовой процедуры и подробно описан, что значительно облегчает его интеграцию в прикладные программы.

Комбинаторные методы используются во многих отраслях. В частности, криптографии, лингвистике, статистике и многих других. Даже в быту мы нередко сталкиваемся с задачами, в которых необходимо выбрать то или иное сочетание из ограниченного числа объектов. Например, расположение книг на полке, расстановка мебели, очередность выполнения дел. В каждой из этих ситуаций человек сравнивает между собой возможные комбинации и выбирает ту из них, которая наиболее полно отвечает определенному критерию.

Для расчета количества комбинаций используют три базовые зависимости.

Рабочие формулы

1. Формула расчета количества перестановок. Перестановками называются комбинации, состоящие из одних и тех же n различных исходных элементов и отличающиеся только порядком расположения элементов [2].

Число возможных перестановок

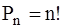,                                                                                                              (1)

где:   n – число переставляемых элементов, n! – факториал числа n.

2. Формула расчета количества размещений. Размещениями назы­вают комбинации, составленные из n различных исходных элементов по m элементов в каждой комбинации, отличающихся либо составом элементов, либо их порядком. В дальнейшем, число элементов в каждой комбинации мы будем называть количеством позиций.

Число возможных размещений

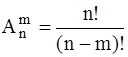.                                                                                                       (2)

Формула расчета количества сочетаний. Сочетаниями называют комбинации, составленные из n различных исходных элементов по m позиций, отличающиеся хотя бы одним элементом. (Порядок элементов не учитывают    12 и 21 считаются одним сочетанием).

Число возможных сочетаний

.                                                                                                  (3)

Важно отметить, что данные формулы справедливы только для выборок с неповторяющимися исходными элементами. Если элементы в выборке повторяются, то расчет проводят по другим формулам.

Выше были названы задачи, в которых необходимо найти не только количество возможных комбинаций, но и сами комбинации. Для этих целей мы разработали на языке программирования MS Visual Basic 6.0 алгоритм, который формирует комбинации перестановок, размещений и сочетаний из заданных последовательностей чисел, букв, символов или любых других объектов, отличающихся между собой по какому-либо признаку.

Описание алгоритма

Алгоритм представляет собой рекурсивную процедуру [3] (т. е. процедуру, вызывающую саму себя с изменяющимися параметрами).

Из блока программы в процедуру обязательно должны пере­даваться следующие переменные и массивы (рекомендуется сделать их глобальными, т. е. видимыми в любой части программы):

· переменная N целочисленного типа. Предназначена для хранения общего количества элементов. Она всегда больше 0;

· переменная M целочисленного типа. Предназначена для хранения количества позиций. Всегда больше 0. Если расчеты проводятся по первой формуле M = N;

· одномерный массив b строкового типа, содержащий N элементов. Перед вызовом процедуры массив заполняется значениями исходных элементов, из которых и составляются комбинации;

· одномерный массив с тоже строкового типа, содержащий N элементов. Перед вызовом процедуры все элементы массива должны иметь значение, равное Empty. Массив предназначен для формирования комбинаций из исходных значений элементов в процессе работы алгоритма;

· одномерный массив znach – строкового типа, содержащий количество элементов, равное количеству комбинаций, вычисленному по рабочей формуле. Перед вызовом процедуры все элементы массива должны иметь значение, равное Empty. Массив предназначен для хранения полученных комбинаций;

· переменная z с типом Long (длинное целое число) – счетчик массива, при вызове процедуры в первый раз, должна иметь значение, равное нулю;

· переменная proverka – логического типа. Если расчеты проводятся по первой или второй формуле, то proverka равна False. Если по третьей формуле –proverka равна True.

Текст алгоритма

Параметры, передаваемые в процедуру при вызове:

· переменная i целочисленного типа. При вызове процедуры из текста программы i всегда равна 1. При рекурсивном вызове перемен­ная i увеличивает своё значение на единицу;

· переменная u целочисленного типа. При вызове процедуры из текста программы u = 1. При рекурсивном вызове переменная u либо не изменяет значение (proverka = False), либо увеличивается на единицу (proverka = True).

Построчное описание алгоритма

1. Работа алгоритма начинается при первом запуске процедуры с параметрами i и u.

2. Вторым шагом является объявление локальных переменных s, k и j, которые мы будем использовать только внутри текущей процедуры. Переменная s накапливает очередную комбинацию из заданных эле­ментов массива B. Переменные k и j используются в качестве счетчиков циклов. В ходе работы процедура вновь и вновь вызывает саму себя. Это приводит к тому, что данная строка повторяется, следо­вательно, значения k и j обнуляются согласно формату оператора Dim.

3. Открываем цикл со счетчиком k, изменяющимся от u до N. Если расчет проводится по первой или второй формулам, то начальное значение переменной-счетчика k при каждом новом входе в процедуру будет изменяться от 1 до N. Цикл служит для определения номера элемента массива b, передаваемого в массив с.

Для того чтобы вывести комбинацию в виде текстовой переменной, а затем присвоить ее значение элементу строкового массива нужно последовательно рассмотреть два условия:

4. Условие 1: Если k-й элемент массива b не равен Empty, т. е. еще не передан в массив c, начинаем проверять условие 2. Если же k-й элемент равен Empty, то рассматриваем следующий элемент массива b.

5. Условие 2: Если i = M, т. е. мы рассматриваем последний элемент составляемой комбинации, начинаем выводить очередную составленную комбинацию. Если рассматриваемый элемент не последний – переходим к пункту 12 и продолжаем дальше собирать комбинацию.

Если оба условия выполняются, то это означает, что очередная ком­бинация собрана и программа выполняет алгоритм вывода комбинации. В приведенном алгоритме комбинации записываются в массив znach. Этот блок реализован в строках 6–11. Если условие 2 не выполняется, то это говорит о том, что комбинация еще не составлена и система производит действия, описанные в строках 12–15.

Для того чтобы вывести комбинацию:

6. Присваиваем k-ое значение массива b i-му значению массива с. Такое решение приводит к тому, что после вывода комбинации в мас­сиве b всегда остается один элемент, значение которого не равно Empty.

7. Обнуляем текстовую переменную s, в которой будет накапли­ваться (собираться) комбинация.

8. Открываем цикл со счетчиком j, изменяющимся от 1 до M.

9. Составляем комбинацию из элементов массива c, путем после­довательного накапливания значений всех элементов массива в одной строковой переменной s.

10. Сформированные комбинации необходимо считать. Эту задачу выполняет счетчик полученных комбинаций z. С каждой итерацией, а точнее шагом рекурсии он увеличивается на единицу.

11. Значение счетчика используется для формирования текстового массива znach, в котором хранятся полученные комбинации. Счетчик служит номером очередного элемента, которому присваивается очередное значение переменной s. После этого управление выходит из конструкции IF и переходит к оператору Next k (16). Значение k увеличивается на 1. Для решения прикладных задач между строкой 11 и оператором Else можно поместить блок анализа каждой комбинации.

12. В строку 12 управление приходит в том случае, если не выполняется условие i = M (5), т. е. пока комбинация не полностью сформирована. Составление комбинации происходит следующим образом: мы передаем значение из k-ой ячейки массива b в i-ую ячейку массива с. Обнуляем b(k) и в зависимости от выбранной формулы (1, 2 или 3) вызываем процедуру CalcCombin. При вызове процедуры счетчик i увеличивается на 1 для любой формулы, а k – только для формулы (3), при работе по формулам (1) и (2) значение этого счетчика при вызове CalcCombin приравнивается к единице.

13. После передачи k-й элемент массива b становится равным Empty.

14. Для нахождения нужного элемента массива b нам нужно переменную i увеличить на единицу. Для этих целей мы используем рекурсию, она выступит в качестве цикла, счетчиком которого является переменная i.

При рекурсивном вызове процедуры, система обязательно выполняет три действия:

а) сохраняет те данные, которые ей понадобятся для продолжения работы после выхода из рекурсии;

б) проводит подготовку к вызову процедуры и передает ей управление;

в) когда вызываемая процедура завершается, система восстанав­ливает данные, сохраненные на первом шаге, и передает управление первому оператору, расположенному за вызовом процедуры CalcCombin (в нашем случае в строку 15).

15. Возвращаем значение i-ой ячейки массива с в k-ую ячейку массива b. Мы воспользовались элементом – вывели комбинацию, а теперь возвращаем элемент на прежнее место.

16. Проверяем значение переменной-счетчика k. Если k = N, то переходим к строке 17, иначе – к строке 3, увеличив значение k на единицу.

17. Точка выхода из процедуры.

Пример использования алгоритма

С помощью описанного алгоритма были получены следующие комбинации перестановок чисел “2”, “4”, “6”, “8” (4!=24):

Таблица 1.

Приведенная процедура может стать основой программ, решающих прикладные задачи, или быть интегрирована как отдельный блок в программные продукты более широкого назначения.