Перколяционная проводимость керметных материалов на основе порошковой смеси проводящего и диэлектрического материалов

Percolation conductivity of cermet materials based on a powder mixture of conductive and dielectric materials

Ye Yint Ko Ko

Post-Graduate Student, Kaluga Branch of Bauman Moscow State Technical University, Russia, Kaluga

Аннотация. Проведены экспериментальные и теоретические исследования влияния объёмных долей проводящей фазы на электрическое поведение керметных материалов. За счет эффекта перколяции происходит резкое снижение удельного сопротивления керметных материалов с концентрацией вольфрама выше 16 об.%.

Abstract. Experimental and theoretical studies were done to examine how the volume fractions of the embedded conducting phase affect the electrical behaviour of cermet materials. Due to the percolation effect, a sharp decrease in the specific resistance of cermet materials with the tungsten concentration higher than 16 vol. %.

Ключевые слова: керметный материал; удельное сопротивление; теория перколяции; электропроводность.

Keywords: cermet material; specific resistance; percolation theory; conductivity.

В соответствии с теорией перколяции частицы проводящей фазы образуют электропроводящие цепочки в изолирующей фазе. С увеличением концентрации проводящей фазы происходит формирование бесконечного кластера, т.е. токопроводящей цепочки, пронизывающей весь объем тела, что сопровождается резким снижением электросопротивления рассматриваемого кермета, называемым порогом перколяции (протекания). Классическая теория протекания с достаточно высокой точностью описывает процесс электросопротивления ниже и выше порога в соответствии с формулировкой

, при ,                                                                                                 (1)

 , при ,                                                                                                 (2)

, при ,                                                                                                (3)

где x – концентрация проводящей фазы; x_c – пороговое значение концентрации проводящей фазы; ρ, ρ_изо., ρ_пров. – удельное электросопротивление композиционного материала, изолирующей фазы и проводящей фазы, соответственно; g, t, s – степенные коэффициенты, связанные между собой выражением: .

Теория прыжковой проводимости позволяет переход электрона от одного донора к другому. В нашей работе частицы вольфрама выступают в качестве доноров. Частицы вольфрама были аппроксимированы сферами. В связи с этим рассматривалась задача сфер теории перколяции [1] для описания пороговых явлений в композиционных материалах.

В рамках этой модели считают, что в пространстве построены сферы с некоторым радиусом, центры которых распределены хаотически в пространстве и в среднем равномерно. Среднее количество центров сфер, которое приходится на единицу объёма, равно N. Если две сферы перекрываются друг с другом, то они считаются связанными. Необходимо найти критическое значение концентрации N, при котором возникает бесконечный кластер связанных друг с другом шаров [2]. Бесконечный кластер будет представлять сетку с расстоянием между узлами порядка , где r_Д – среднее расстояние между донорами (). В теории прыжковой проводимости такая сетка называется критической.

Рисунок. Зависимость удельного сопротивления керметов от объёмной доли проводящей фазы

Модель «сетка сопротивлений» используют для расчётов критической концентрации. Эта модель формулируется на языке обыкновенных электротехнических сопротивлений. Предположим, что сопротивление между каждой парой доноров включено. Сами доноры с определенной окрестностью можно воображать в виде узлов, к которым припаяны проволочки от большего количества сопротивлений. Другой конец каждого из этих сопротивлений припаян к другому узлу. В результате получится беспорядочная трёхмерная сетка сопротивлений c периодом R_c.

Сопротивления, включённые между донорами, должны быть вычислены, исходя из туннельного тока, который течёт между этими донорами при заданном электрическом поле. В связи с этим, решение этой задачи сводится к решению квантово-механической задачи [2, 3]:

 ,                                                                                                                (4)

где R₀ – собственное сопротивление частиц проводящей фазы, r_c – расстояние между узлами,  – размер агломератов проводящей фазы. Сопротивления между различными частицами проводящей фазы могут сильно отличаться друг от друга, по этой причине аппроксимируем все сопротивления максимальным значением R_mаx.

Для того чтобы получить удельное электросопротивление, необходимо умножить полное сопротивление кубика R_max на площадь его грани () и разделить на длину ребра (R_c):

 .                                                                                                         (5)

Считаем, что каждый агломерат имеет диаметром  нм, а r_c – это радиус сферы, т.е. расстояние между узлами. Значение r_c напрямую связано с объёмной концентрацией проводящей фазы выражением: 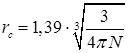 [74]. В работе рассматривалась трехмерная задача для образцов композиционных материалов. Была найдена зависимость удельного электросопротивления от концентрации проводящей фазы на пороге протекания, описываемая выражением [2]:

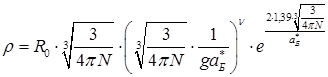 ,                                                                                            (6)

где R₀ – собственное сопротивление частиц проводящей фазы, N — объёмная концентрация проводящей фазы. Пользуясь предложенных в работе [2] диапазоном значений коэффициента ν, было подобрано значение для трехмерной задачи (ν = 0.8). На рис. 1 представлена зависимость удельного сопротивления керметов от объёмной концентрации проводящей фазы. Из графика видно, что материалы при малых концентрациях проводящей фазы (объёмная доля проводящей фазы менее 16%) являются диэлектриками, а при дальнейшем увеличении объёмной концентрации вольфрама наблюдается снижение электросопротивления на несколько порядков.

Выводы. Таким образом, получены керметные материалы на основе вольфрам и нитрида алюминия. Теоретически и экспериментально найдена зависимость электропроводности таких керметных материалов от объёмной доли проводящей фазы. Такая зависимость носит пороговой характер. Определен порог перколяции 0,16 об.% W для изученных керметных материалов.