Определение запаса устойчивости модели ракеты-носителя

DETERMINATION OF THE STABILITY RESERVE OF THE LAUNCH VEHICLE MODEL

Maxim Arevkov

Assistant, Amur State University, Russia, Blagoveshchensk.

Ruslan Buzikov

Student, Amur State University, Russia, Blagoveshchensk.

Alexander Voronkov

Student, Amur State University, Russia, Blagoveshchensk

Аннотация. Одной из востребованных задач, решаемых при постройке ракет, является стабилизация, т. е. обеспечение устойчивого полета по необходимой траектории. Устойчивость модели ракеты – это способность возвращаться в положение равновесия, при его нарушении внешними силами.

Abstract. One of the required problems to be solved in the design of model rockets is stability, that is ensuring a stable flight on the required trajectory. Stability of the model rocket is the ability to return to the equilibrium position when it is disturbed by external forces.

Ключевые слова: модель ракеты; устойчивость; твердотопливный ракетный двигатель; центр тяжести; центр давления.

Keywords: model rockets; stability; solid rocket motors; centre of gravity; centre of pressure.

Цель исследования: определить запас устойчивости модели ракеты-носителя, построенной на тематической смене «Морской старт» в ВДЦ «Океан».

В данном исследовании использован аэродинамический метод обеспечения устойчивости. Суть этого метода заключается в изменении аэродинамических сил, действующих на модель ракеты в полёте. Аэродинамическая устойчивость зависит от взаимного расположения центра тяжести (ц.т.) и центра давления (ц.д.).

Предположим, что в нашем распоряжении две ракеты. Первая (рисунок 1.а) выполнена таким образом, что ее ц. д. находится впереди ц.т., а у второй (рисунок 1.б) ц.д. расположен позади ц.т. Допустим, что под действием возмущающих сил эти ракеты повернулись вокруг ц.т. на одинаковый угол. Рассмотрим, как будет вести себя каждая из моделей ракет. При изменении угла атаки ракеты, в ц.д. появится аэродинамическая сила R, которую можно разложить на две силы: осевую – F и нормальную N. Так как осевая сила F проходит через ц.т., то никакого момента относительно ц.т. она не создает. Нормальная сила создает относительно ц.т. момент M, действие которого для первой ракеты направлено на увеличение угла атаки, а для второй ракеты для уменьшения угла атаки до начального положения. Такой момент M называется стабилизирующим. Ракета (рисунок 1.а) является неустойчивой так, как под действием момента M, ракета будет увеличивать угол атаки и изменять свою траекторию, что является недопустимым. Ракета (рисунок 1.б) является устойчивой так, как под действием момента M, ракета будет уменьшать угол атаки до первоначального и придерживаться заданной траектории.

Можно сделать вывод, что аэродинамическая стабилизация обеспечивается только в том случае, когда ц.д. расположен сзади ц.т. ракеты.

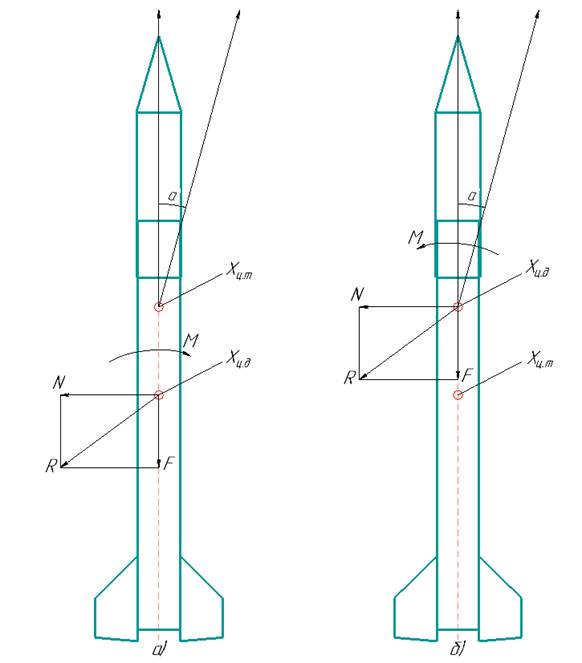
Рисунок 1. Влияние взаимного расположения ц. т. и ц. д. на устойчивость модели ракеты

а – модель устойчивая в полете; б – модель неустойчивая в полете.

Задачей данной модели ракеты-носителя является вывод полезной нагрузки на высоту 80-150 метров.

Чертеж модели ракеты представлен на рисунке 2.

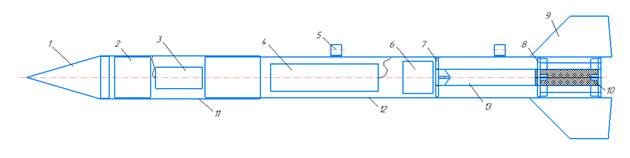
Рисунок 2. Модель ракеты

1 – конусообразный обтекатель; 2 – полезная нагрузка; 3 – парашют отсека полезной нагрузки; 4 – парашют модели ракеты-носителя; 5 – направляющие; 6 – пыж; 7 – якорь; 8 – шпангоуты; 9 – стабилизаторы; 10 – РДТТ; 11 – отсек полезной нагрузки; 12 – корпус модели ракеты-носителя; 13 – отсек для установки двигателя.

Определение положения центра тяжести ракеты-носителя из распределительного свойства центров тяжести.

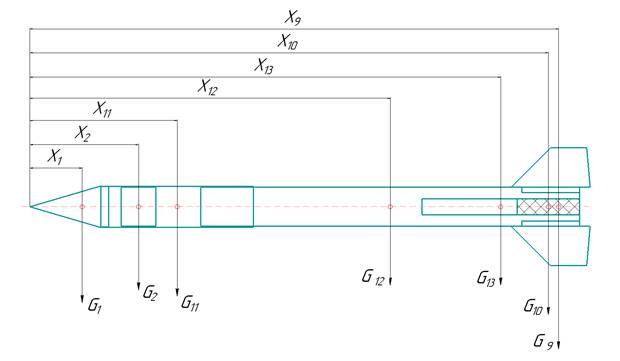
Рисунок 3. Чертеж модели ракеты для определения центра тяжести

В расчете пренебрегаем элементами ракеты-носителя с незначительной массой.

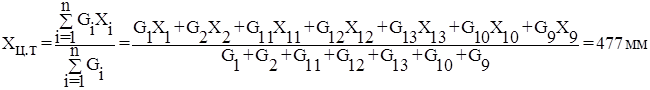
Определение положения центра давления ракеты-носителя методом площадей.

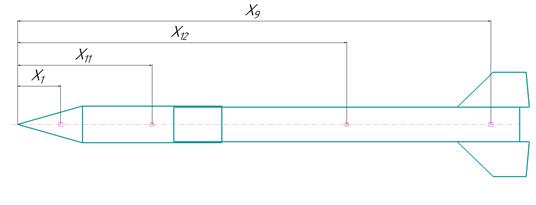
Рисунок 4. Чертеж модели ракеты для определения центра давления

Вычисление запаса устойчивости.

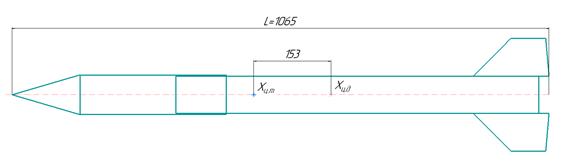
Рисунок 5. Чертеж модели ракеты для определения запаса устойчивости

Исходя из данных расчетов видно, что исследуемая модель ракеты является устойчивой. Запас устойчивости лежит в допустимых пределах.  

Также рассчитаем высоту полёта модели.

Для расчета высоты полёта модели ракеты будем использовать баллистические уравнения, с помощью которых можно приближенно, но довольно точно определить числовое значение.

Для расчета понадобятся характеристики двигателя.

Был использован твердотопливный ракетный двигатель (РДТТ) от компании Real Rockets, со следующими техническими характеристиками:

Таблица

Технические характеристики РД1-50-5М

Максимальная высота полета модели ракеты — это сумма высоты активного и пассивного участков полёта:

;

;

 ;

 ;

;

.

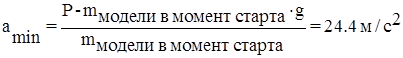По результатам расчетов, видно, что требуемая задача по высоте выполняется.