Возможности быстрого решения транспортной задачи

Формулировка транспортной задачи

Формулировку транспортной задачи можно найти в книгах по линейному программированию, или содержащих раздел – линейное программирование.

Задача линейного программирования заключается в определении решения неопределенной системы линейных уравнений, при котором целевая функция достигает наименьшего, или наибольшего значения. Решение заключается в определении первого опорного плана и перехода к оптимальному плану.

Транспортная задача

Однородный продукт, сосредоточенный в m пунктах отправления в количествах а₁,а_2, …а_м единиц соответственно необходимо доставить в каждый из n пунктов назначения в количествах b₁, b₂ …b_n. Общий запас продукта в пунктах отправления равен суммарной потребности в этом продукте пунктов назначения. Обычно пунктов назначения больше пунктов отправления. n>m.

Стоимость перевозки единицы продукта из i - того пункта отправления в j – й пункт назначения равна с_ij и известна для всех комбинаций {I,j}. {I,j} – маршрут перевозки из i  того пункта отправления к j тому пункту назначения. xij – количество продукта перевозимого по маршруту {I,j}.

Условия транспортной задачи записывается в виде таблицы перевозок, таблицы стоимостей перевозок по различным маршрутам и выражения целевой функции.

Наличие матрицы стоимостей перевозок дает возможность значительно упростить решение задачи и быстро получить оптимальный план перевозок.

Таблица 1.

Таблица перевозок

Таблица 2.

Таблица стоимостей перевозок

Выражение для целевой функции C=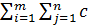 _ij*x_ij

Запас продукта в i - том пункте отправления измеряется величиной a_i. Потребность в продукте j-того пункта назначения равна b_j.

Задача заключается в определении таких величин x_ij, для всех перевозок {I,j}, при которых суммарная стоимость перевозок была бы минимальной.

Пример № 1

Предприниматель имеет центры распределения, находящиеся в Атланте, Чикаго и Нью – Йорке. Эти центры имеют в распоряжении соответственно 40, 40, 40 единиц некоторого однородного товара. Рынкам сбыта требуются следующие количества единиц товара: Кливленду 25, Луисвиллю 20, Мемфису 30, Питтсбургу 30 и Ричманду 15. Стоимость перевозки единицы товара между каждым центром и рынком в долларах указана в следующей таблице.

Таблица 3.

Суммарный объем товара в пунктах отправления равен 120 единицам и равен суммарным потребностям в пунктах назначения. Пример заимствован из книги [2] списка литературы. Прежде всего, на этом примере покажем, что условие транспортной задачи можно записать в виде системы линейных уравнений. Затем запишем формулировку транспортной задачи в матричном виде, сформулируем теорему построения опорного плана и учитывая матрицу стоимостей перевозок найдем оптимальный план.

Запишем развернутую систему уравнений

Всего 8 уравнений. Но линейно независимых 7. Если сложить уравнения от 4 до 8 и вычесть сумму уравнений от 2 до 3, то получим первое уравнение. Таким образом одно из восьми уравнений, мы получили первое, линейная комбинация остальных. Исключим первое уравнение и систему запишем в матричном виде A*X = P0.

Где А – матрица размером 7 на 15 с элементами равными 1 и 0. Х – матрица – строка определяемых объемов перевозок между пунктами отправления и пунктами назначения. P₀ – матрица–столбец объемов продукта в пунктах отправления и потребностей в пунктах назначения. С – матрица-строка стоимостей перевозок.

Вектор X = {x _11, …, x_{in ,} …, x₂₁  … x_3n  … x_m1  … x_mn  }              

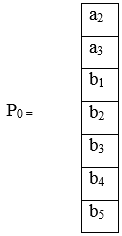
C = {c_11…c_ij,…c_mn }

Формулировка транспортной задачи приводится к такому виду

A*X = P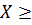₀

0

C*X - минимум

Сформулируем теорему построения опорного плана транспортной задачи. Пусть для определенности n > m.

Теорема

Существует план, содержащий не менее n и не более, чем m+n-1 положительных перевозок x_ij. При этом система векторов P_ij, соответствующих таким перевозкам линейно независима.

План перевозок должен содержать не менее n не нулевых значений, чтобы обеспечить потребности в пунктах назначения.

Мы предлагаем при решении задачи опираться на принцип организации перевозок по маршрутам с минимальной стоимостью перевозок.

В каждом столбце определяется маршрут с наименьшей стоимостью перевозок и назначается значение перевозок равное b_j. Если в столбце имеются равные значения стоимостей перевозок, то перевозки назначаются по маршруту, которому соответствует большее a_i. В этом столбце остальные перевозки принимаются нулевыми.

Составляется матрица перевозок с последним столбцом равным a_i- 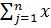 _ij.

Таблица 4.

Так-как a₁ –b_{2 =} a₂ –b₂ =20, то x₁₂ = x₂₂ =10

Для каждой строки определена разность a_{i - 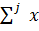ij}

Для получения опорного плана осталось привести к равенству количества перевозимого товара и заданных значений в пунктах отправления. Перемещение по столбцам выполняется с учетом стоимостей перевозок. Так в третьей строке уменьшаем x₃₄ на 5 единиц, перемещая их в ячейку [2,4].

Получим опорный план.

Таблица 5.

Значение целевой функции 3625; План содержит 7 не нулевых значений x_ij.

Выполняется утверждение теоремы построения опорного плана m+n -1 = 7

Проверим опорный план на оптимальность.

На маршрутах с не нулевыми перевозками стоимость перевозки запишем в виде суммы

c_ij = u_i + v_j. Полученная система уравнений неопределенная и имеет множество решений.

Примем одну переменную равной минимальному значению соответствующих с_ij

Подсчитаем косвенные значения стоимостей перевозок с*_шо = u_ш + v_о. На маршрутах с не нулевыми перевозками косвенные стоимости равны значениям в таблице стоимостей перевозок. Поэтому косвенные стоимости подсчитываем только для нулевых перевозок. Если косвенные стоимости не превышают значений в таблице стоимостей перевозок, то план оптимальный.

c*₁₁ =u₁ + v₁ = 35

c*₁₄ = u₁ + v₄ = 45

c*₁₅ =u₁ + v₅ = 40

c*₂₃ = u₂ + v₅ = 40

c*₂₅ = u₂ + v₅ = 40

c*₃₁ = u₃ + v₁ = 25

c*₃₂ = u₃ + v₂ = 20

c*₃₃ = u₃ + v₃ = 30

Так как все косвенные стоимости не превышают соответствующих значений в таблице стоимостей, то полученный план оптимальный. Получили оптимальный план без дополнительных итераций.

Пример 2

Таблица 6.

Таблица перевозок

Таблица 7.

Таблица стоимостей перевозок

В каждом столбце по маршрутам с минимальной стоимостью перевозок планируем перевозки в объемах, определяемых пунктами назначения. В последнем столбце записываем отклонения объема товара в пунктах отправления и планируемых перевозок.

Таблица 8.

Составим таблицу с вакантными местами для изменения плана перевозок

Таблица 10.

План, обеспечивающий заданные перевозки

Таблица 11.

Проверим план на оптимальность   

Система уравнений имеет множество решений. Требуется найти решение, в котором все переменные неотрицательные.

Подсчитываем косвенные стоимости.

c*₁₂ =u₁ + v₂ = 15 + 20 - 35

c*₁₃ = u₁ + v₃ = 15 + 25 = 40

c*₁₄ =u₁ + v₄ = 15 +35 = 50

c*₂₁ = u₂ + v₁ = 5 + 10 = 15

c*₂₃ = u₂ + v₃ = 5 + 25 = 30

c*₂₅ = u₂ + v₅ = 5 + 25 = 30

c*₃₁ = u₃ + v₁ = 0 + 10 = 10

c*₃₂ = u₃ + v₂ = 0 +20 = 20

Косвенные стоимости не превышают соответствующих значений в таблице стоимостей перевозок. План оптимальный.

Подсчитаем среднюю стоимость перевозок найденного плана.

C_ср = {x₁₁ * c₁₁ + x₁₅ * c₁₅ + x₂₂ * c₂₂ + x₂₄ * c₂₄ + X₃₃ * c₃₃ + x₃₄ * c₃₄ + x₃₅ * c₃₅} / 90 =

{ 20 * 25 = 10 * 40 + 15 * 25 + 5 * 40 + 30 * 25 + 5 * 35 = 5 * 25 } / 90 = 28

Средняя стоимость перевозок меньше минимальной стоимости по маршрутам, не входящим в план перевозок.

План содержит m + n – 1 = 3 + 5 – 1 = 7 не нулевых перевозок.

Пример 3

Таблица 12.

Таблица перевозок

Таблица 13.

Таблица стоимостей перевозок

Минимальные стоимости в столбцах сразу определяют оптимальный план перевозок.

Таблица 14.

В этом примере число не нулевых перевозок равно числу пунктов назначения.

Выводы

1. Предлагаемый алгоритм решения транспортной задачи состоит из четырёх шагов:

В каждом столбце назначаются перевозки в объемах, требуемых пунктами назначения по маршрутам с наименьшей стоимостью перевозок. 

Подсчитывается столбец отклонений запаса продукта в пунктах отправления при первом шаге решения задачи.

Исправляется план перевозок распределением товара в столбцах с учетом требований обнуления столбца отклонений и стоимостей перевозок по различным маршрутам.

Проверяется план на оптимальность.

Выполнение первого и третьего шагов решения задачи с учетом матрицы стоимостей перевозок позволяет достаточно быстро найти оптимальный план перевозок.

2. Для любой транспортной задачи существует план. Существует план, содержащий не менее n и не более чем m+n-1 положительных перевозок x_ij. При этом система векторов P_ij, соответствующих таким перевозкам линейно независима.

3. Подсчет средней стоимости перевозок менее трудоемкий по сравнению с решением неопределенной системы линейных уравнений. Поэтому, если средняя стоимость планируемых перевозок меньше любого значения элемента матрицы стоимости, соответствующего нулевым перевозкам, то план перевозок оптимальный. В других случаях следует проверять план на оптимальность сравнением косвенных стоимостей перевозок с заданными.