ПРОЕКТИВНАЯ ГЕОМЕТРИЯ В 3D ТЕХНОЛОГИЯХ

Статья посвящена использованию современных 3D технологий для визуального представления основных теорем проективной геометрии.

В наши дни активно развиваются технологии, позволяющие представлять различного рода визуальную информацию в трехмерном, четырехмерном и даже пятимерном пространстве. Область трехмерного моделирования и анимации активно совершенствуется и в образовании, что вооружает преподавателя высококачественными учебными материалами, экономя, таким образом, время на объяснение сложных понятий; визуализирует «сложные» темы программы, помогая обучающимся лучше понимать изучаемый материал; повышает мотивацию к обучению; способствует усвоению большего объема информации.

В связи с этим является актуальным использование 3D технологий при обучении проективной геометрии.

В настоящий момент, в свободном доступе имеется большое количество различных программ, поддерживающих функцию 3D моделирования и интерпретации различной графической информации в формате анаглифной, поляризационной и других 3D технологий. В данной статье мы рассмотрим элементарные и доступные способы применения 3D технологий в процессе изучения основной теоремы проективной геометрии – теоремы Дезарга: если прямые, соединяющие соответственные вершины двух трехвершинников  пересекаются в одной точке S, то точки пересечения соответственных сторон этих трехвершинников лежат на одной прямой.

Задача конструирования теоремы Дезарга в 3D технологиях была разбита на следующие этапы:

1.  Конструирование чертежа к теореме;

2.  Анимирование чертежа к теореме;

3.  Представление чертежа в анаглифной 3D технологии.

1.  Конструирование чертежа к теореме.

При конструировании чертежа к теореме Дезарга мы пользовались кроссплатформенной динамической математической программой GeoGebra.

GeoGebra – бесплатная математическая программа, обладающая множеством возможностей в области геометрии, алгебры, различных вычислений, позволяющая строить графики, чертежи, кривые, выполнять действия с матрицами, комплексными числами, работать с таблицами и многое другое.

1)  Запустив программу GeoGebra, в строке меню выберем команду Вид → Полотно 3D (рис. 1).

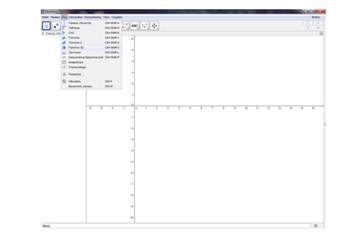
Рисунок 1. Рабочее окно программы GeoGebra

2)  В появившемся поле создадим требуемый чертеж, начав с основных точек построения. Для этого в появившемся меню примитивов будем выбирать необходимые инструменты (Точка \ Прямая \ Перпендикуляр \ Многоугольник и т. д.) (рис. 2).

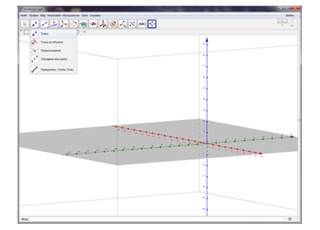
Рисунок 2. Создание чертежа

3)  Все построенные объекты можно перемещать в пространстве рабочего поля с помощью указателя мыши. Изменять размер, цвет, толщину объектов в зависимости от необходимости, можно с помощью команды: правая кнопка мыши (по интересующему объекту) → Свойства. В меню Свойства, выбирая нужную вкладку, выполним необходимые преобразования объекта. При необходимости можно удалять ненужные объекты с помощью команды: правая кнопка мыши (по интересующему объекту) → Удалить.

Для удобства работы с чертежом, в меню инструментов выберем: Вращать чертеж. С помощью данной команды можно выполнить вращения построенного чертежа под удобным углом.

При необходимости, для предотвращения загруженности чертежа, можно воспользоваться следующими командами. В основном меню выберем команду: Настройки →Дополнительно. В появившемся окне выберем вкладку «Настройки − Полотно 3D».

Сняв галочку с пункта «Показывать оси» можно отменить отображение координатных осей на чертеже. С помощью вкладки «Цвет полотна» можно изменить цвет рабочей зоны. Вкладка Clipping (ограничение) отвечает за границы выполняемого чертежа. Сняв галочку с пункта «Use clipping (использовать ограничения)» можно отменить использование наложенных ограничений на данный чертеж. Сняв галочку с пункта «Show clipping (отображать ограничения)» можно отменить отображение ограничений данного чертежа. Вкладка «Clipping box size (размер границ ограничений)» отвечает за размер отображаемого чертежа. По своему желанию можно выбрать соответствующий размер чертежа. Используя предлагаемые программой инструменты, завершаем все необходимые построения по данному чертежу (рис. 3).

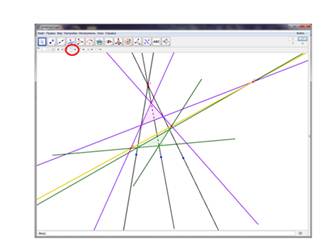
Рисунок 3. Анимирование чертежа

Также, с помощью иконки «Начать или прекратить вращать вид», на дополнительной строке инструментов, можно задать вращение построенного чертежа с необходимой скоростью.

2.  Анимирование чертежа к теореме.

Изучение основных проективных теорем может быть проиллюстрировано GIF-анимацией, демонстрирующей пошаговое выполнение чертежей, относящихся к решению конструктивных задач с помощью конструкций проективных теорем, либо самих теорем и следствий из них. Для создания подобной GIF-анимации по готовым изображениям мы воспользовались программами Easy GIF Animator и Bandicam.

Easy GIF Animator – это простой инструмент для создания анимированных GIF изображений.

Bandicam – приложение для захвата видео с экрана монитора, а также и для снятия скриншотов в высоком качестве.

Итак, процесс создания всей необходимой GIF-анимации и видеофайлов к теореме Дезарга выглядит следующим образом:

1)  при помощи программы Bandicam создадим серию скриншотов, иллюстрирующих пошаговое создание чертежа к теореме Дезарга. Для создания подобных скриншотов, во время работы с программой GeoGebra, запустим программу Bandicam. При запуске данной программы, открывается два окна: основное окно программы и рабочая рамка для снятия фото и видео. В основном окне программы Bandicam, в строке «Папка вывода», укажем путь к папке, в которую желаем сохранить все сделанные фото и видео: D:\Геометрия\Теорема Дезарга.

Свернем основное окно программы, оставив рабочую рамку. Можно настраивать размеры рабочей рамки с помощью курсора мыши в соответствии с той областью, которую мы собираемся снимать. Открыв программу GeoGebra и не сворачивая рабочей рамки программы Bandicam, выполним построение необходимого чертежа. Сделаем скриншот каждого шага построения с помощью соответствующей иконки фотоаппарата в правом верхнем углу рабочей рамки программы Bandicam (рис. 4).

Во время построения не обязательно сворачивать рабочую рамку, т.к. она не влияет на процесс построения и не мешает ему. После создания необходимых скриншотов, можно открыть папку, указанную в строке «Папка вывода» и просмотреть их.

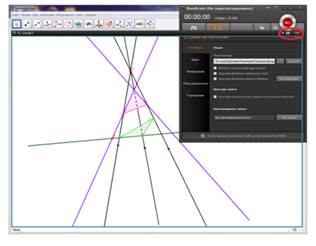
Рисунок 4. Создание серии скриншотов

Для создания видеофайла к соответствующему чертежу, активируем функцию вращения чертежа в программе GeoGebra, нажатием на иконку «Начать или прекратить вращать вид». Нажав в правом верхнем углу рабочей рамки иконку «REC», активируем запись видео. Для прекращения записи повторно нажмем на иконку «REC».

2)  Используем программу Easy GIF Animator для создания необходимой GIF-анимации из полученной серии скриншотов. Запустим программу Easy GIF Animator и в появившемся окне выберем пункт «Создать новую анимацию». В открывшемся основном окне программы (окно подсказок можно закрыть), слева выберем вкладку «Вставить изображение (F3)». В появившемся окне найдем папку с сохраненными скриншотами и выберем первый скриншот. Аналогичным образом, в соответствующем порядке, импортируем в программу все необходимые скриншоты. С помощью вкладки «Свойства анимации» можно настроить количество повторов созданной анимации и фон рабочей области. Пользуясь вкладкой «Свойства кадра» можно установить желаемую скорость смены выбранных кадров (рис. 5):

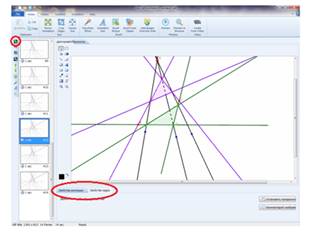
Рисунок 5. Создание GIF-анимации

С помощью команды (File → Save), сохраним созданную GIF-анимацию в необходимую папку.

3.  Представление чертежа в анаглифной 3D технологии.

Для создания видеофайлов в формате 3D воспользуемся соответствующими возможностями программы GeoGebra, позволяющими переводить готовые чертежи в анаглифный 3D формат.

1)  Откроем созданный чертеж относящейся к теореме Дезарга в программе GeoGebra. На дополнительной строке инструментов выберем иконку «Выбрать тип проекции», и воспользуемся функцией “Projection for glasses”, для отображения данного чертежа в анаглифном 3D формате (рис. 6):

Воспользовавшись командой (Настройки →Дополнительно), и выбрав вкладку «Настройки − Полотно 3D», можно перейти к настройкам типов проекции. В открывшемся окне выберем вкладку «Projection». В строке «Очки», можно настроить изображение в соответствии с такими параметрами, как: расстояние между линзами, отображать изображение в цветном или в черно-белом формате.

2)  Приведем полученный чертеж в движение при помощи иконки «Начать или прекратить вращать вид» и, воспользовавшись программой Bandicam, создадим соответствующий видеофайл в формате 3D, относящийся к теореме Дезарга. Технология создания подобных видеофайлов была рассмотрена выше.

Также можно пользоваться готовым чертежом в программе GeoGebra для представления различных теорем. Это позволит в режиме реального времени изменять чертеж в зависимости от необходимости.

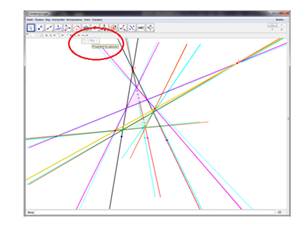
Рисунок 6. Представление чертежа в анаглифном 3D формате

При просмотре полученного 3D видеофайла необходимо воспользоваться соответствующим оборудованием, например, анаглифные 3D очки любого формата.

Рассмотренные приемы интерпретации проективной геометрии в 3D технологиях, легко могут быть применены для создания необходимого наглядного материала при изучении различных теорем и проективных задач.