ВРЕМЕННЫЕ РЯДЫ В ПОСТПРОГНОЗЕ ПАВОДКА ДАЛЬНЕГО ВОСТОКА 2013 года

Летом и осенью 2013 года на Дальнем Востоке прошел катастрофический паводок. Данная работа студентов ТОГУ посвящена построению модели паводка по временным рядам уровня рек Дальнего Востока.

По данным на июль—сентябрь 2011, 2012 и 2013 годов вначале были построены линейные модели паводка рек Амур, Бира, Зея, Уркан [1; 2; 3; 5]. Построение моделей велось с помощью табличного процессора MS Excel. Этот модуль позволяет выполнить статистический анализ выборочных данных [4]. Режим работы Регрессия этого модуля осуществляет вычитание коэффициентов линейной множественной регрессии с k переменными, построение доверительных интервалов и проверку значимости уравнения регрессии. Построенные линейные модели существенно отличаются от реальных значений. Это обусловлено тем, что в создании модели невозможно предугадать появление случайных параметров, таких как аномальные изменения циркуляции воздушных масс над югом российской Сибири и Дальним Востоком (увеличение амплитуды волн России), снежная зима в районе бассейна Амура и поздняя весна. Однако эти параметры могут оказать колоссальное влияние на рассматриваемое явление.

При построении полиномиальных моделей результаты оказались лучше. Стоит отметить, что полиномиальная аппроксимация используется для описания величин, попеременно возрастающих и убывающих. Она полезна, например, для анализа большого набора данных о нестабильной величине. Степень полинома определяется количеством экстремумов (максимумов и минимумов) кривой. Полином второй степени может описать только один максимум или минимум. Полином третьей степени имеет один или два экстремума. Полином четвертой степени может иметь не более трех экстремумов.

Так для реки Бира в городе Биробиджан полиномиальная модель представлена на рис. 1 для 2011 года и на рис. 2 для 2012 года.

Для реки Уркан возле города Зея полиномиальная модель представлена на рис. 3 для 2011 года и на рис. 4 для 2012 года.

Для реки Зея в районе г. Благовещенска полиномиальная модель представлена на рис. 5 для 2012 года.

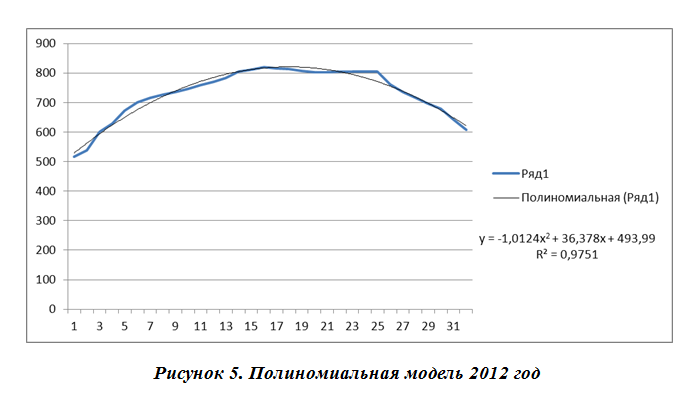
 Для реки Амур в районе г. Комсомольск-на-Амуре полиномиальная модель представлена на рис. 6 для 2011 года и на рис. 7 для 2012 года.

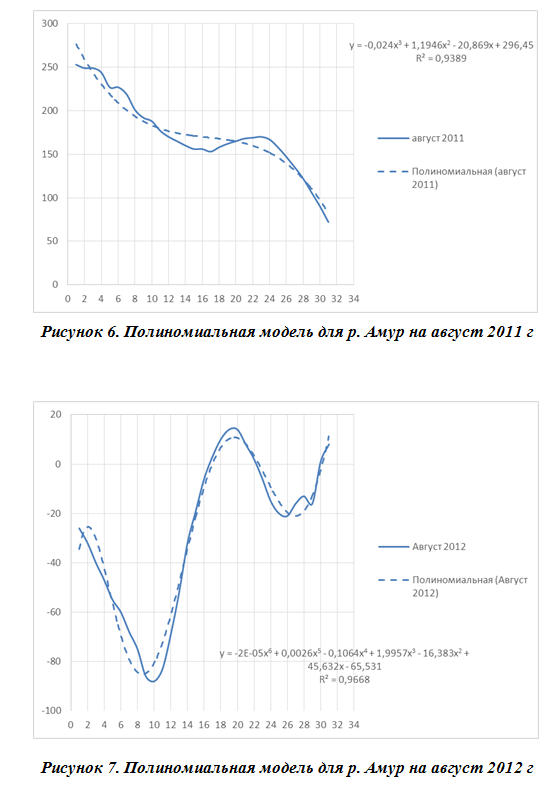
При построении краткосрочного пргноза более адекватными оказались также нелинейные модели для рассматриваемых рек.

На рис. 8 представлена полиномиальная модель для реки Бира в городе Биробиджан на август 2013 года.

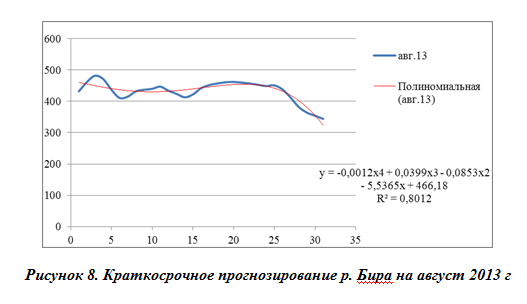
По данному графику можно увидеть, что полиномиальная модель является адекватной, следовательно, дает нам право краткосрочного прогнозирования.

Для реки Уркан возле города Зея полиномиальная модель на август 2013 года представлена на рис. 9.

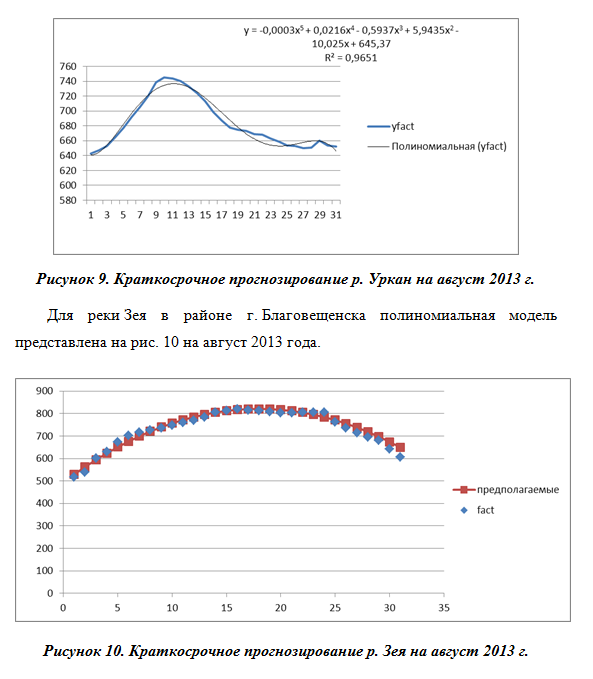
Для реки Амур в районе г. Комсомольск-на-Амуре были рассмотрены линейная и логарифмическая модели (рис. 11).

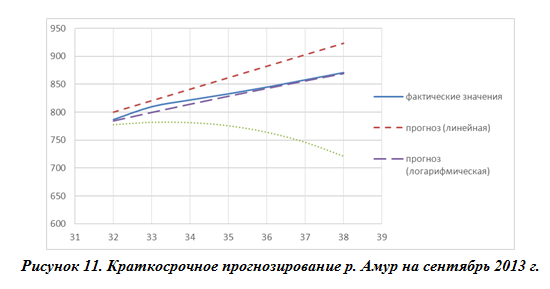
 Для реки Амур в районе г. Хабаровска были построены линейная и экспоненциальная модели (рис. 12).

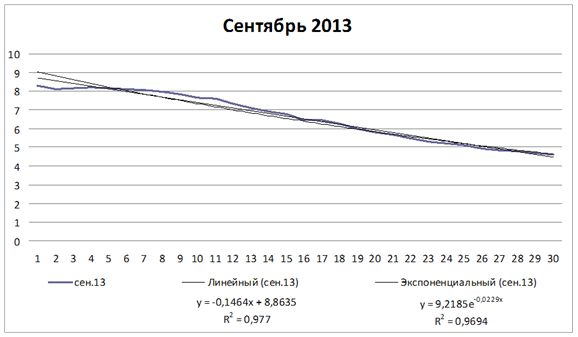
Рисунок 12. Краткосрочное прогнозирование р. Амур на сентябрь 2013 г.

При краткосрочном прогнозировании только нелинейные модели довольно хорошо справилась с поставленной задачей. Это объясняется несколькими причинами. Для улучшения точности прогнозов, по словам ученых из Института водных проблем Российской академии наук, необходимо расширять сеть гидрологических постов. Так, на Амуре, где осенью этого года произошло рекордное наводнение с печальными последствиями, действует лишь два пункта замера расхода воды. Один из них находится в селе Богородском, второй — в Хабаровске. Получаемых с этих пунктов данных ученым недостаточно не только для точных прогнозов, но и для адекватной оценки происходящего непосредственно в момент наводнений.

Список литературы:
1.    График хода уровней поста Биробиджан [Электронный ресурс]. — Режим доступа: URL: http://lifelikbez.ru/ (дата обращения: 07.12.13).
2.    График хода уровней поста в близи Комсомольска-на-Амуре [Электронный ресурс]. — Режим доступа: URL: http://lifelikbez.ru/r.php?navSelect=http%3A%2F%2Flifelikbez.ru%2Fr.php%3Foutput_type%3Dflash%26recordID%3D5805&navSelect2=http%3A%2F%2Flifelikbez.ru%2Fr.php%3Foutput_type%3Dflash%26recordID%3D5019&output_type=flash&current=&aver=&d0=01&m0=06&y0=2013&d1=01&m1=09&y1=2013&recordID=5024&draw_type=graph (дата обращения: 07.12.13).
3.    Новостной портал Хабаровского края [Электронный ресурс]. — Режим доступа: URL: http://www.dvhab.ru (дата обращения: 07.12.13).
4.    Обработка экспериментальных данных в MS Ecel: методические указания к выполнению лабораторных работ для студентов дневной формы обучения/ сост. Е.Г. Агапова, Е.А. Битехтина. — Хабаровск: Изд-во Тихоокенаский государственный университет, 2012. — 32 с.
5.    Оперативная информация, ГУ МЧС России по Еврейской Области [Электронный ресурс]. — Режим доступа: URL: http://www.79.mchs.gov.ru/forecasts/index.php?PAGEN_2=3 (дата обращения: 07.12.13).