КОЛИЧЕСТВО ОБРАЗУЮЩИХ МАТРИЦ ЦИКЛИЧЕСКОГО (N, K) КОДА, ИСПРАВЛЯЮЩЕГО ОШИБКИ КРАТНОСТИ S

В данной статье автором проведено исследование о количестве образующих матриц циклического (n, k) кода, исправляющего ошибки кратности S. Подсчитаны общее количество образующих матриц (n, k) кода, количество образующих матриц систематического (n, k) кода и их отношение.

Передачей информации можно назвать своего рода физический процесс, посредством которого осуществляется перемещение информации в пространстве и времени.

Для того чтобы перенести информацию в пространстве и времени, её представляют форме сообщения. Сообщение же всегда представляется в виде сигнала. Построение сигнала по определенным правилам, обеспечивающим соответствие между сообщением и сигналом, называют кодированием.

Если понимать кодирование в широком смысле, то это преобразование сообщения в сигнал. Кодирование в узком смысле — это представление дискретных сообщений определенными сочетаниями символов.

Одним из наиболее важных кодов является циклический код. Циклические коды применяются при записи на CD и DVD, при передаче аудио и видео информации, при использовании USB-портов для обмена информацией.

Циклический код — это линейный код, обладающий свойством цикличности. Иначе говоря, каждая циклическая перестановка кодового слова также является кодовым словом. Циклический код является разновидностью группового кода и не отличается от него по уровню помехозащищенности.

Циклические коды легко реализуются технически. Именно поэтому они нашли широкое применение. Также циклические коды незаменимы при необходимости передачи информации по каналам связи, в которых отсутствует возможность повторной передачи.

При кодировании сообщений длинная последовательность обычно формируется из кодовых комбинаций, каждая из которых соответствует одному знаку. Число символов, из которых составлена такая кодовая комбинация, называется длиной кода.

Количество передаваемых дискретных сообщений — объем кода — и заданная корректирующая способность являются исходными данными для построения группового кода.

Количество информационных разрядов k по заданному объему кода Q определяется из условия

2^k -1>= Q                                                                                  (1)

Каждой из 2^k-1ненулевых информационных последовательностей нужно поставить в соответствие n-разрядный избыточный код — разрешенную комбинацию.

Чтобы обеспечить возможность определения и исправления ошибок кратности до S включительно, должно выполняться неравенство

                                                                    (2)

Длину кода n при кодировании k информационных разрядов определим из неравенства (2).

Образующая матрица — это матрица, которая состоит k линейно независимых строк. Каждая из этих строк является разрешенной кодовой комбинацией. Остальные разрешенные комбинации могут быть представлены в виде линейной комбинации строк образующей матрицы.

Если код должен быть систематическим, то образующая матрица представляется в виде двух блоков: единичной матрицы и матрицы-дополнения. Строки матрицы-дополнения определяются путем вычисления многочленов r (x) для каждой строки, то есть делением на образующий многочлен g (x).

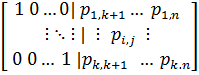M_n,k=[E_kP_k,n-k]=                                                     (3)

Из формулы (1) видно, что для кодов, исправляющих различное количество ошибок при одинаковых k, будут разные значения n. Образующая матрица так же будет менять размерность, однако это всегда будет матрица размера (n, k) для любых n, k и S.

Перестановка строк (столбцов) образующей матрицы приводит к эквивалентному коду с той же корректирующей способностью. Таким образом, чтобы посчитать количество образующих матриц для заданного образующего многочлена, нужно посчитать количество всех возможных перестановок строк и столбцов.

Формула подсчета количества перестановок из m элементов P_n =m·(m−1)·(m−2)...3·2·1 = m! (4)

Зафиксируем строки на своих местах.

Таблица 1.

Образующая матрица

Количество всех перестановок столбцов будет равняться n!

Поменяем местами две строки и снова зафиксируем.

Таблица 2.

Образующая матрица c двумя переставленными строками

Количество всех перестановок столбцов также будет равняться n!

Таблица 3.

Образующая матрица, в которой переставлены i-тая и i+1 строки

Для этой перестановки строк количество перестановок столбцов так же будет n!

Таким образом, для каждой из k! перестановок строк будет n! перестановки столбцов, то есть будет k!*n! всех возможных перестановок строк и столбцов.

Если код должен быть систематическим, то переставлять местами мы можем только последние n-k столбцов. То есть всего будет (n-k)! Образующих матриц систематического кода.

Тогда, для заданного образующего многочлена отношение количества матриц систематического кода к количеству всех образующих матриц будет равно

Список литературы:

1. Дмитриев В.И. Прикладная теория информации. Учебник для студентов ВУЗов по специальности «Автоматизированные системы обработки информации и управления». — М.: Высшая школа, 1989 — 320 с.

2. Евсеев А.И Передача информации — [Электронный ресурс] — Режим доступа. — URL: http://peredacha-informacii.ru/.

3. Прохоров В.С. Теория информации Лекции — [Электронный ресурс] — Режим доступа. — URL: http://profbeckman.narod.ru/Informat.files/Teorinf.pdf.

4. Фурсов В.А. Лекции по теории информации: Учеб. пособие под редакцией Н.А. Кузнецова –Самара: Изд-во СГАУ,2006. – 148с.