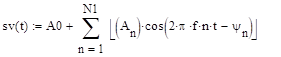ОЦЕНКА ЛИНЕЙНЫХ ИСКАЖЕНИЙ ШИРОКОПОЛОСНОГО СИГНАЛА ПРИ НИЗКОЧАСТОТНОЙ ФИЛЬТРАЦИИ

При работе всех систем передачи информации ставится задача не допустить значительных искажений передаваемого сигнала в процессе его распространения по системе. Эти искажения могут возникать вне устройств канала связи (работа других передающих устройств, атмосферные процессы электрической природы и т.д.) и в самих устройствах канала связи (нелинейные преобразования сигнала, несоответствие характеристик линейных блоков спектральным характеристикам сигнала и т.д.). В данной работе исследовалось искажение широкополосного сигнала в линейных блоках, связанных со спадом усилении в области верхних частот. Такой спад наблюдается у всех реальных линейных цепей по ряду причин, в частности в связи с паразитными параметрами элементов.

Была составлена программа в среде Mathcad, позволяющая проводить восстановление временной функции сигнала по его спектру, оценивать погрешность восстановления временной функции при ограниченной ширине спектра сигнала, проводить цифровую фильтрацию сигнала, строить графики временных функций и спектральных характеристик.

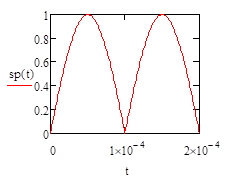
В качестве примера сигнала был рассмотрен вариант двухполупериодного выпрямления гармонического колебания. На рис. 1 представлены графики временной функции и амплитудного спектра этого сигнала:

Рисунок 1. График временной функции и амплитудного спектра

Восстановление сигнала по известным параметрам спектра производилось по формулам (1).

Восстановление сигнала проводилось с помощью ряда Фурье (2).

В реальной жизни говорить о сигналах с бесконечно широким спектром нельзя, так как даже если бы такие сигналы и существовали, то, проходя по реальным электрическим цепям с конечной полосой пропускания, они неизбежно превратились бы в сигналы с ограниченным спектром. Поэтому для сигналов нужно ограничить реальную ширину спектра. Конечно, исключение из рассмотрения каких-то частот скажется на точности представления временной функции. Но всегда можно выбрать верхнюю границу так, чтобы возникающая при этом погрешность не была слишком большой. Активной шириной спектра как раз и называют полосу частот, которая содержит основную информацию о сигнале [1]. Для оценки активной ширины спектра исследуемого сигнала рассчитывалась среднеквадратическая погрешность восстановления сигнала по ограниченному числу гармоник N. График этой зависимости приведен на рис 2.

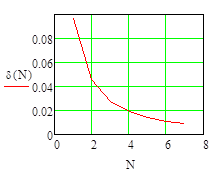
Рисунок 2. Зависимость среднеквадратичной погрешности от числа гармоник

Из графика видно, что вначале рост числа суммируемых гармоник приводит к быстрому снижению погрешности восстановления, а затем погрешность уменьшается все медленнее. За предельный уровень погрешности восстановления был выбран 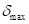=0.01. Для достижения погрешности меньше указанной величины в синтезе должно участвовать 8 гармоник спектра. Поэтому активная ширина спектра исследуемого сигнала составит Fa = 8F, где F – частота первой гармоники в спектре сигнала.

Далее рассмотрим фильтрацию исследуемого сигнала цифровым фильтром нижних частот (ФНЧ) с частотой среза, равной Fa, большей Fa, и меньшей Fa.

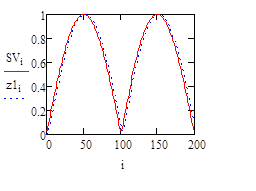
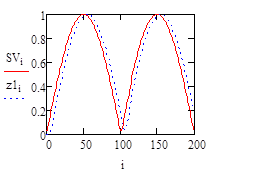
Рисунок 3. График входного сигнала и отклика, а) Fc = 4Fa; б) Fc = 2Fa;

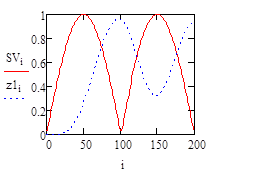
Рисунок 4. График входного сигнала и отклика, а) Fc = Fa; б) Fc = 0.5Fa; в) Fc =0.125Fa

Видно, что на всех графиках рис. 3 и рис. 4 сигнал на выходе фильтра запаздывает относительно входного и имеет место искажение графика в зоне максимально быстрого изменение функции. На рис. 3а и 3б этих изменений практически нет, на рис. 4а и 4б изменения все больше и больше. Стоит отдельно рассмотреть рис. 4в на котором видно, что, фильтр срезает все гармоники кроме первой и получаем сигнал, состоящий только из 1 гармоники с высокой погрешностью, запаздыванием, сильными искажениями в зоне максимально быстрого изменения функции.

Теперь можно рассмотреть на рис. 5 график ошибки восстановления сигнала отклика в зависимости от частоты среза фильтра.

Рисунок 5. Зависимость ошибки восстановления от частоты среза

По графику видно, что чем больше частота среза, тем лучше восстанавливается график. И в зависимости от ошибки восстановления можно подобрать нужную частоту среза, при этом учесть весь активный спектр сигнала.

Чтобы сигнал, проходя через устройство с ограниченной со стороны верхних частот полосой пропускания не испытывал заметных искажений, верхняя граничная частота полосы пропускания должна быть не менее активной ширины спектра сигнала, а желательно и выше.
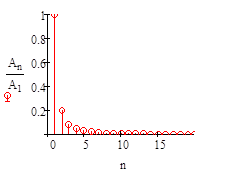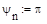