КРАЕВАЯ ЗАДАЧА С ПЕРИОДИЧЕСКИМИ ГРАНИЧНЫМИ УСЛОВИЯМИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ

Постановка задачи:

Пусть  заданные непрерывные функции, удовлетворяющие условиям, указанным ниже:

Пусть заданы константы , и поскольку ,

где 

Рассмотрим следующую начально-краевую задачу:

Теорема 1. Пусть Let  выполнено начальное условие (1). Тогда начально-краевая задача (1)–(3) имеет единственное решение

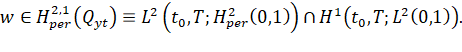
Априорные оценки: Лемма 1. Для всех  выполняется следующее неравенство:

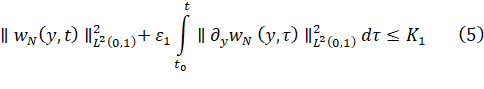
где .

По исходно заданной задаче :

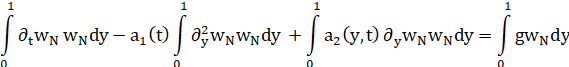
 по определению нормы

   .

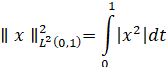
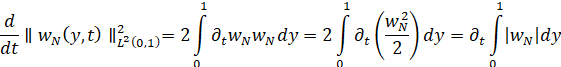
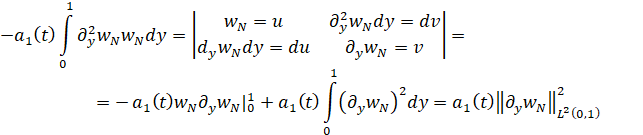
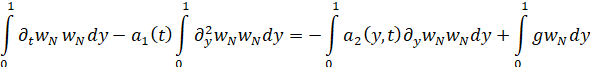
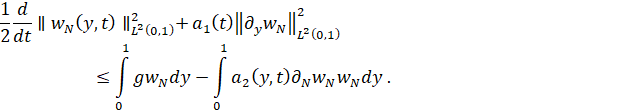
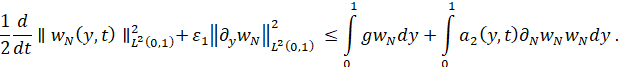
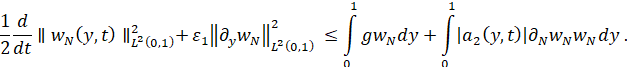
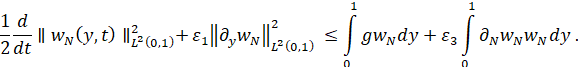
С помощью неравенства Коши–Буняковского

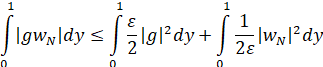
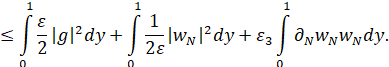
Лемма доказана.

Лемма 2. Для всех  выполняется следующее неравенство:

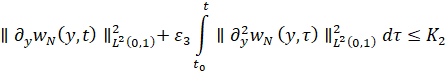
где  .

Лемма 3. Для всех  выполняется следующее неравенство:

где константа, не зависящая от  и выполнено условие (1). Тогда начально-краевая задача (2)–(4) имеет слабое решение в пространстве .

Лемма 4. При условиях Леммы 3 решение начально-краевой задачи единственно и принадлежит пространству .