Сравнительный анализ многослойного и нечеткого многослойного персептронов при решении задачи классификации

Введение. Человек ежедневно сталкивается с проблемами классификации. Например, администратор в банке решает, следует выдать кому-то кредит или нет. В данном случае администратор классифицирует клиентов по степени риска: высокий, средний или низкий риск. При оптическом распознавании символов сканируемые символы также ассоциируются с соответствующими им классами. Имеется немало вариантов изображения буквы «Н» даже для одного конкретного шрифта – символ может оказаться, например, смазанным, – но все эти изображения должны принадлежать классу «Н» [1].

Задача классификации – задача, в которой имеется множество объектов, разделенных некоторым образом на классы. Требуется построить алгоритм, способный классифицировать произвольный объект (указать номер класса, к которому относится данный объект) из исходного множества [2]. Одним из вариантов решения такой задачи является использование искусственных нейронных сетей.

Нейронные сети можно рассматривать как современные вычислительные системы, которые преобразуют информацию по образу процессов, протекающих в мозгу человека [3].

Нейронные сети оказались очень полезными при решении задач распознавания образов и классификации объектов. Они способны решать задачи, в которых неизвестны зависимости между входными и выходными данными [1].

В данной работе для решения задачи классификации используются многослойный и гибридный нечеткий многослойный персептроны. Исследованы классифицирующие способности этих нейронных сетей различной конфигурации.

Основная часть. Наиболее популярный класс многослойных сетей прямого распространения образуют многослойные персептроны, в которых каждый вычислительный элемент использует в качестве функции активации сигмоидальную функцию или гиперболический тангенс. При этом многослойный персептрон в целом может формировать сколь угодно сложные границы принятия решения, несмотря на то что элементы по отдельности имеют очень ограниченные вычислительные возможности [4]. Разработка алгоритма обратного распространения ошибки для определения весов в многослойном персептроне сделала эти сети наиболее популярными у исследователей и пользователей нейронных сетей.

Гибридный нечеткий многослойный персептрон является модификацией классического многослойного персептрона с дополнительным слоем с нечеткой самоорганизацией. Благодаря наличию нечеткого слоя нечеткий многослойный персептрон способен определять степень принадлежности входного вектора к одному из возможных классов, что позволяет решать задачи с пересекающимися классами. Структура нечеткого многослойного персептрона представлена на рисунке 1.

 
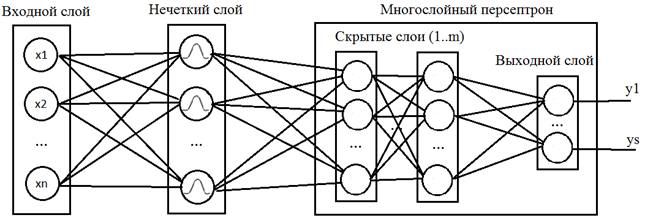
Рисунок 1. Структура нечеткого многослойного персептрона

Для обучения многослойного персептрона выбран алгоритм обратного распространения ошибки. Алгоритм обратного распространения ошибки определяет стратегию подбора весов многослойной сети с применением градиентных методов оптимизации. В настоящее время считается одним из наиболее эффективных алгоритмов обучения многослойной сети. При обучении ставится задача минимизации целевой функции, формируемой, как правило, в виде квадратичной суммы разностей между фактическими и ожидаемыми значениями выходных сигналов, которая для P обучающих выборок определяется по формуле:

                                                                                            (1)

где P – количество обучающих векторов, M – количество нейронов в выходном слое. Уточнение весов может проводиться после предъявления каждой обучающей выборки [5].

Для обучения нечеткого многослойного персептрона выбран алгоритм нечеткой самоорганизации C-Means. Цель обучения алгоритма состоит в таком подборе центров  , чтобы для заданного множества обучающих векторов  обеспечить достижение минимума функции

,                                                                                             (2)

при одновременном соблюдении условий ограничения

,                                                                                                                 (3)

где M – количество центров, P – количество входных векторов [6].

Результаты.

В качестве выборки для обучения и тестирования нейронной сети были выбраны данные с датчиков, фиксировавших положение некоторой детали автомобиля в пространстве при прохождении различных дорожных покрытий. Характеристика обучающей выборки:

−         всего 18000 записей;

−         5 входных параметров: номер типа детали, номер детали, три координаты;

−         6 классов дорожных покрытий.

Обучение нейронной сети осуществлено с помощью метода обратного распространения ошибки. Обучение нечеткого слоя нечеткого многослойного персептрона произведено с помощью алгоритма нечеткой самоорганизации C-means. Размеры входного и выходного слоев для всех экспериментов установлены в соответствии с количеством атрибутов и классов. Наборы разбиты на обучающую и тестовую выборки в соотношении 7 к 3. После каждого эксперимента массив входных данных перемешивается и все веса нейронной сети обнуляются.

Исследование зависимости погрешности обучения от значения коэффициента обучения представлено на рисунке 2.

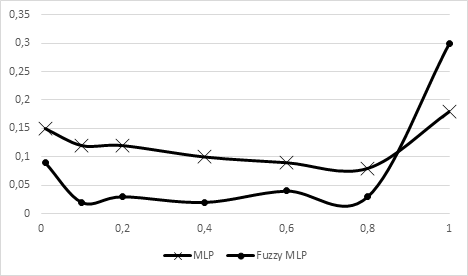
Рисунок 2. График зависимости погрешности обучения от значения коэффициента обучения

Исследование зависимости погрешности классификации от числа итераций обучения представлено на рисунке 3.

Рисунок 3. График зависимости погрешности классификации от числа итераций обучения

Исследование зависимости погрешности классификации от числа нейронов скрытого слоя представлено на рисунке 4.

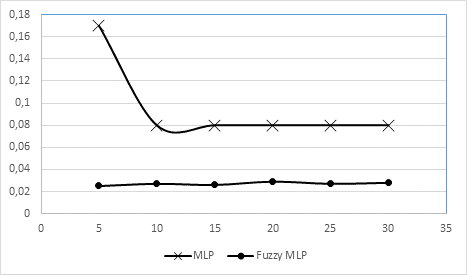
Рисунок 4. График зависимости погрешности классификации от числа нейронов скрытого слоя

Выводы. Таким образом, нечеткий многослойный персептрон показал более точные результаты в сравнении с многослойным персептроном. Однако, обучение нечеткого многослойного персептрона требует большего числа итераций и больших затрат памяти вычислительной машины.