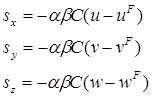Метод погруженных тел для численного моделирования задач строительной аэродинамики

Последние 15-20 лет в регионах России наблюдается стремительный рост и уплотнение городской застройки за счет возведения зданий весьма смелых архитектурных форм и оригинальных конструктивных решений и их компактных комплексов, что способствует появлению необходимости в доработках и развитии существующих методик определения ветровых нагрузок и воздействий на здания, сооружения и комплексы.

Идеология «метода погруженных тел» заключается в создании расчетной модели, состоящей из двух доменов (воздушного домена и домена с твердыми телами). Далее для каждого домена создается расчетная сетка, и домен с твердыми телами «погружается» в воздушный домен (т.е. решается задача с несогласованными сетками).

Термин «погруженные тела» (перевод с англ. Immersed Solid) «погруженные граничные условия» впервые определен Ч. Пескиным (C.Peskin). В его работе предложен и реализован подход к моделированию потока крови вокруг сердечного клапана на декартовых сетках, не повторяющих геометрическую форму сердца. Влияние погруженных границ определялось специальной функцией в уравнениях, описывающих течение среды. В дифференциальные уравнения добавляются члены- источники, моделирующие твердое тело(«методы штрафных функций»).

«Погруженное тело» представлено как значение источника в уравнениях сохранения импульса. Размер исходного значения контролируется с помощью специального параметра – коэффициент масштабирования источника импульса (Momentum Source Scaling Factor).

Чтобы учесть пограничный слой и идентифицировать «погруженные границы» для жидкости, находящейся внутри «погруженной границы» устанавливаются вынуждающие значения (forcing terms). Чтобы лучше проанализировать это воздействие границ существует возможность применять измененные вынуждающие значения вблизи погруженной границы. Эти вынуждающие значения вычисляются с помощью параметра модель границы (Boundary Model) с измененным значением вынуждающего члена и устанавливаются параметры отслеживание границ (Boundary Tracking). Для вычисления вынуждающих значений, необходимо определить ближайшую точку на погруженной границе для каждого пристеночного узла. При этом будет включается один из двух алгоритмов поиска. Какой алгоритм поиска будет использоваться, зависит от того, какой вариант выбран для параметра отслеживание границ (Boundary Tracking):1) поиск по элементам (Search Through Elements) или 2) вытеснение очертания границ (Boundary Face Extrusion).

Алгоритм поиска вытеснение очертания границ имеет преимущество нахождения нормального направления стенки в физическом пространстве, но успех этого алгоритма зависит от расстояния, на котором очертания границ вытеснены вдоль нормального направления стенки.

При использовании метода «поиск по элементам», важно, чтобы длина элементов сетки погруженного тела в направлении, нормальном к погруженной границе, была больше, чем длина элементов сетки жидкости вблизи погруженной границы, таким образом, чтобы внутристеночные узлы, как правило, попадали в наружный слой элементов границы погруженного тела. При использовании этого параметра, будет выполняться поиск по элементам вблизи погруженной границы и проецирование узлов жидкости вблизи погруженной границы на очертания границ или вершинах элемента погруженного тела. Недостаток этого варианта заключается в том, что проекция осуществляется в вычислительном пространстве так, что, по сравнению с другим вариантом, нормальное направление будет, как правило, менее точным.

Погруженное тело является твердотельным объектом, который перемещается в текучей среде. Погруженный твердотельный объект занимает такой же объем пространства как часть текучей среды, которая содержит погруженное тело. Для того чтобы смоделировать воздействие погруженного тела на окружающую жидкость, в уравнение импульса добавляют значения источника импульса:

u, v и w– это три компонента скорости жидкости, а 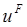 ,  и 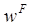–  это компоненты вынуждающей скорости, связанной с погруженным телом. Коэффициент источника импульса С– это большое число, которое определяется как среднее значение трех диагональных коэффициентов в уравнении импульса. Кроме того,  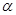 - это коэффициент масштабирования силы импульса (Мomentum Force Scaling Factor), для которого устанавливается значение по умолчанию, равное 10.0. Соответствующий параметр коэффициента масштабирования источника импульса (Momentum Source Scaling Factor) – это баланс между точностью и надежностью. Более высокое значение этого коэффициента приводит к решению задачи с большей точностью, но меньшей надежностью, и возникают проблемы со сходимостью.

Присутствие погруженного тела в поле потока моделируется с помощью специальной вынуждающей функции 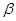. Если пристеночное моделирование вблизи границ погруженного тела не используется, функция  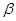устанавливается равной 0 – для узлов жидкости, лежащих за пределами среды погруженного тела и равной 1 – для узлов жидкости внутри погруженного тела. В противном случае функция  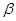определяется как функция среднего внутреннего объема таким образом, чтобы значения  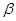и соответствующие вынуждающие значения вблизи погруженной границы не были равны нулю. Функция среднего внутреннего объема равняется в среднем внутренней функции, взвешенной по объему узла.

Решатель автоматически обновляет положение сетки погруженного тела в начале каждой итерации и затем определяет список узлов жидкости, которые лежат внутри данного погруженного тела. Решатель применяет источники погруженного тела к узлам жидкости, которые лежат внутри погруженного тела, для того чтобы привести скорость жидкости в соответствие со скоростью погруженного тела.

Значения источника импульса, добавленные в уравнение импульса жидкости, моделируют массовое поведение потока жидкости вокруг твердотельного объекта. Однако возникают определенные сложности при отслеживании границы погруженного тела, связанные с моделированием пограничного слоя вблизи границ погруженного тела. Для этого применяются измененные вынуждающие значения вблизи погруженных границ.

Рисунок 1. Обозначения узлов вблизи границ погруженного тела

На рисунке 1 показана схема границ погруженного тела (обозначена красной линией) с обозначением близлежащих узлов. Условные обозначения (метки) также приведены в таблице 1. Оранжевой стрелкой на рисунке показано нормальное направление стенки, соответствующее заданному узлу NW. Для каждого узла NW решатель выполняет поиск по окружающим узлам жидкости и определяет соответствующий узел FL, используя процедуру, в которой учитывается нормальное расстояние от погруженной границы и отклонение от нормального направления.

Таблица 1.

Условные обозначения узлов вблизи границ погруженного тела