ТЕОРИЯ ИГР. ИГРЫ С ПРИРОДОЙ

Очень часто в процессе состязательной деятельности, примерами которой являются спортивные соревнования, судебные процессы или военные маневры, возникают ситуации, когда интересы сторон не совпадают либо являются прямо противоположными. Изучением подобных «конфликтов» занимается теория игр — раздел математики, занимающийся разработкой рекомендаций по наиболее оптимальному алгоритму действий конфликтующих сторон. Эта теория применима к большинству экономических ситуаций. Выигрышем в данной ситуации является эффективное использование факторов производства, максимизация прибыли, минимизация издержек.

В рамках данной теории называют упрощенную математическую модель конфликтной ситуации, подчиняющуюся определенным правилам. Иными словами, это — набор правил, определяющих возможные действия игроков. Если участников двое, актуально использование матричной игры, представленной в виде матрицы, отражающей выигрыш первого игрока и проигрыш второго.

В большинстве матричных игр интересы сторон противоположны, а действия каждой из них направлены на увеличение собственного выигрыша, либо увеличение проигрыша конкурента. Но в некоторых ситуациях имеется неопределенность из-за отсутствия информации об условиях, в которых осуществляются действия: погоде, потребительских предпочтениях и пр. Эти условия не зависят от действий игроков, а определяются внешними факторами. Такие игры называются играми с природой. Человек (первый игрок) в них старается действовать осмотрительно, а природа (второй игрок) — случайно.

Выбор оптимальной стратегии в играх с природой определяется рядом критериев, таких как:

1.  Критерий Вальда. Стратегия выбирается из условия max_i(min_j a_ij) и совпадает с нижней ценой игры. Игрок исходит из предположения о том, что природа будет действовать наихудшим для него образом, поэтому данный критерий считается пессимистическим.

2.  Критерий максимума является оптимистическим и выбирается из условия max_i(max_ja_ij).

3.  Критерий Гурвица рекомендует стратегию, определяемую по формуле max_i(A*min_j a_ij + (1-A)*max a_ij), где А — степень оптимизма и изменяется в пределах от 0 до 1. Критерий придерживается промежуточной позиции, учитывающей возможность как наихудшего, так и наилучшего поведения природы. При А=0 данный критерий можно заменить критерием максимума, а при А=1 — критерием Вальда. Величина критерия А зависит от степени ответственности игрока: чем она выше, тем ближе А к единице.

4.  Критерий Сэвиджа. Суть его заключается в выборе стратегии, не допускающей слишком высоких потерь. Для этого используется матрица рисков, элементы которой отражают убытки, которые понесет игрок в том случае, если для каждого состояния природы не будет выбрано наилучшей стратегии.

R =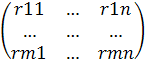

Элементы этой матрицы находятся по формуле:

r_ij = max_i a_ij — a_ij, где max_i a_ij — максимальный элемент в столбце исходной матрицы.

Оптимальная стратегия определяется выражением min_i(max_j r_ij).

Если решение принимается в условиях неопределенности, то лучше использовать несколько критериев. В том случае, если рекомендации совпадают, можно с уверенностью выбирать наилучшее решение. Если рекомендации противоречивы, решение надо принимать более взвешенно, с учетом сильных и слабых сторон.

Пример. Предприятие может выпускать 3 вида верхней одежды: пальто (A₁), крутки (A₂), ветровки (A₃). Прибыль от продаж товара каждого вида определяется состоянием спроса, на который существенное влияние оказывают погодные условия, которые могут принимать 3 формы: (B₁), облачная (B₂) и ясная (B₃). Зависимость дохода предприятия от вида продукции и погодных условий представлена в таблице (млн. руб):

Таблица 1.

Зависимость дохода предприятия

Тогда платёжная матрица A имеет вид:

А =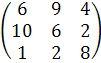

Элемент матрицы A — (a_ij) показывает, какой доход может получить фирма с, если она будет выпускать товар i (i =1, 2, 3), а погода будет находиться в состоянии j (j = 1, 2, 3).

Необходимо определить пропорции, в которых предприятие должно выпускать продукцию из имеющегося материала, чтобы получить максимальный гарантированный доход вне зависимости от погодных условий.

Данная задача может быть сведена к антагонистической игре: в качестве первого игрока выступает предприятие, а в качестве второго — природа. Предположим, что природа может вести себя таким образом, чтобы минимизировать выгоду фирмы, преследуя, таким образом, противоположные интересы (это предположение позволяет оценить доход фирмы при максимально неблагоприятных погодных условиях). В этом случае фирма имеет в своём распоряжении три чистые стратегии:

1.  производить только пальто;

2.  производить только куртки;

3.  производить только ветровки;

Как игрок, природа может использовать три возможные стратегии:

1.  дождливую погоду (B₁);

2.  облачную погоду (B₂);

3.  ясную погоду (B₃).

Решение:

1.  Проанализируем платёжную матрицу A.

А =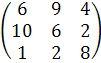

Матрица A не имеет доминируемых стратегий, следовательно, упростить ее нельзя

2.  Проверим, имеет ли данная игра седловую точку.

Найдём нижнюю и верхнюю цену игры:

V_*=max_i min_ja_ij = 4.

V^*=min_jmax_ia_ij = .

V_* ≠V^*, поэтому данная антагонистическая игра не имеет седловой точки, а, следовательно, и решения в чистых стратегиях.

3.  Решение игры следует искать в смешанных стратегиях. Сведём ее к задаче линейного программирования. Если предприятие применяет свою оптимальную смешанную стратегию P^*, а природа применяет последовательно свои чистые стратегии, то математическое ожидание дохода, который фирма может получить, будет не меньше цены игры V. Следовательно, должна выполняться следующая система неравенств:

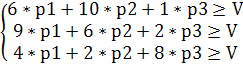
Разделим каждое из неравенств, входящих в систему на V и введём новые переменные:

y_{1 =} ; y_{2 =} ; y_{3 =}

Поскольку p1+ p2+ p3= 1, новые переменные удовлетворяют условию:

y1 + y2 + y3 = 1/V

В результате получим новую систему неравенств:

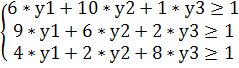
Поскольку цель первого игрока — максимизация его выигрыша, а математическое ожидание его выигрыша не меньше цены игры, он будет стремиться максимизировать цену игры, что эквивалентно минимизации величины 1/V.

Таким образом, для первого игрока задача об определении оптимальной стратегии поведения свелась к задаче линейного программирования:

F(y_i) = y₁ + y₂ + y₃ → min

при следующих функциональных ограничениях:

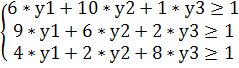
и прямых ограничениях:

y₁ ≥ 0, y₂≥ 0, y₃≥ 0

Далее рассмотрим второго игрока — природу. Если будет применять свою оптимальную смешанную стратегию Q^*, а первый игрок — предприятие будет последовательно применять свои чистые стратегии, то математическое ожидание проигрыша второго игрока не будет превышать цены игры. Следовательно, должна выполняться следующая система неравенств:

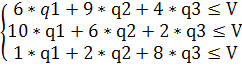
Разделим каждое из неравенств, входящих в систему на V и введём новые переменные:

x1=; x2=; x3=

Поскольку q1+ q2+ q3= 1, новые переменные удовлетворяют условию:

x1 + x2 + x3 = 1/V

В результате получим новую систему неравенств:

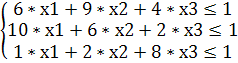
Поскольку цель второго игрока — минимизация проигрыша, а математическое ожидание его проигрыша не больше цены игры, то второй игрок будет стремиться минимизировать цену игры, что эквивалентно максимизации величины 1/V.

Таким образом, для природы задача об определении оптимальной стратегии поведения свелась к задаче линейного программирования:

F'(x_i) = x₁ + x₂ + x₃ → max

при следующих функциональных ограничениях:

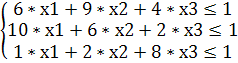
и прямых ограничениях:

x₁ ≥ 0, x₂ ≥ 0, x₃ ≥ 0

Таким образом, для того чтобы найти оптимальную смешенную стратегию второго игрока, необходимо также решить задачу линейного программирования.

Задачи обоих игроков свелись к паре двойственных задач линейного программирования:

Таблица 1.

Задачи линейного программирования

Задача первого игрока решается симплекс-методом. Результаты счёта:

y1 = 0,0524; y2 = 0,06; y3 = 0,0838; V = 5,093

p1 = 0,267; p2 = 0,307; p3 = 0,426; F(yi) = 0,1962

Задача второго игрока решается также симплекс-методом. Результаты счёта:

x1 = 0,0157; x2 = 0,0688 x3 = 0,1126; V = 5,093

q1 = 0,08 q2 = 0,347; q3 = 0,573; F'(xi) = 0,1971

Вывод: в соответствии с полученными результатами предприятию гарантирован средний доход в размере 5,093 млн. у. е. при самых неблагоприятных условиях. Оптимальная стратегия для него — производство всех трех видов одежды, причем пальто должны составлять 26,7 % выпуска, куртки — 30,7 %, а ветровки — 42,6 %.

Влияние дождливой погоды на ассортимент и доходы фирмы составляет 8 %, облачной — 34,7 %, а ясной — 57,3 %.

Предлагаем также выбрать единственную оптимальную стратегию при помощи описанных ранее критериев.

1.  Критерий Вальда

max_i(min_j a_ij) = max (4; 2; 1) = 4.

Согласно критерию Вальда, следует производить пальто.

2.  Критерий Сэвиджа. Построим матрицу рисков:

R =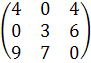

min_i(max_j r_ij) = min (4; 6; 9) = 4

Согласно критерию Сэвиджа, следует производить пальто.

3.  Критерий Гурвица. Предположим, что А = 0,5.

max_i(A*min_j a_ij + (1-A)*max a_ij) = (6,5; 6; 4,5) = 6,5

Согласно критерию Гурвица, также рекомендуется производить пальто.

4.  Если принять известным распределение вероятностей наступления различных погодных условий, условно приняв каждую их равной 1/3, для принятия решения можно найти математическое ожидание выигрыша.

M1 = 6/3+9/3+4/3 = 19/3

M2 = 10/3+6/3+2/3 = 18/3

M3 = 1/3+2/3+8/3 = 11/3

Так как максимальное математическое ожидание имеет М1, следует производить пальто.

Следует отметить, что вариант оптимальной стратегии, полученный при помощи критериев, не совпадает с рассчитанным ранее. Это связано с тем, что данный метод позволяет выбрать стратегию, подразумевающую производство только одного товара с минимальными потерями, в то время как первоначальный способ ориентирован на расчет оптимальной пропорции между всеми группами производимых товаров.

Список литературы

1.            Дубров А.М., Лагоша Б.А., Хрусталев Е.Ю. Моделирование рисковых ситуаций в экономике. М.: «Финансы и статистика», 1999. — 172 с.

2.            Каплан А.В., Каплан В.Е., Мащенко М.В., Овечкина Е.В. Решение экономических задач на компьютере. М.: «ДМК-Пресс», 2004. — 594 с.

3.            Чупрынов Б.П. Методы оптимизации в экономике. Часть 2. Самара: «СГЭУ», 2000. — 106 с.

4.            Экономико-математические методы и модели. / Под ред. Макарова С.И. — М.: «Кнорус», 2009. — 238 с.