ВЫБОР ОПТИМАЛЬНОГО ВАРИАНТА КАПИТАЛОВЛОЖЕНИЙ ПРИ СТРОИТЕЛЬСТВЕ ЗАВОДА ПО ПЕРЕРАБОТКЕ МУСОРА

В процессе человеческой деятельности возникают обстоятельства, в которых потребности, стремления участников либо прямо противоположны, либо вовсе не совпадают, не будучи непримиримыми.

Теория игр ― раздел математики, изучающий конфликтные ситуации на основе математических моделей, разрабатывающий рекомендации для принятия наиболее оптимальных решений каждым из участников в ходе конфликта, т.е. таких действий, которые бы обеспечили сторонам наилучший результат. В экономике многим ситуациям можно придать игровую схему. Выигрышем могут быть эффективность применения ограниченных ресурсов, основных фондов, уровень прибыли, себестоимость и т. д.

Однако в отдельных задачах имеется неопределенность, причиной появления которой служит отсутствие информации об условиях, в которых осуществляется действие. Они зависят от объективной действительности, а не от осознанных поступков другого игрока. Такие игры называются играми с природой. Человек в таких обстоятельствах старается действовать осторожно, вторая сторона действует случайно.

Условия игры задаются матрицей —

Пусть игрок А имеет стратегии А₁, А₂, ..,А_m, а природа ― состояния В₁, В₂, …, В_n. Самой элементарной является ситуация, если известна p_{j ―} вероятность наступления каждого состояния природы B_j. При этом, если приняты во внимание все возможные состояния, р₁+р₂+…+р_j+…+р_n=1.

Если игрок А придерживается чистой стратегии А_i, то математическое ожидание выигрыша составит р₁*a_i1+р₂*a_i2+…+р_n* a_in. Наиболее выгодной будет та стратегия, при которой достигается

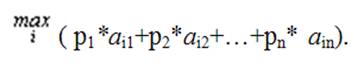
Если информация о состояниях с природой незначительна, то можно использовать принцип недостаточного основания Лапласа, согласно которому можно считать, что все состояния природы имеют равные вероятности:

,

Т. е. стратегию, для которой среднее арифметическое элементов соответствующей строки максимальное.

В регионе необходимо построить завод по переработке мусора. В данном регионе имеются возможности:

a₁ ― строительство мусороперегрузочной станции;

a₂ ― строительство современного мини-завода с использованием пиролизной установки;

a₃ ― строительство мусоросжигательного завода.

Возможные решения A = {a_1, a_2, a₃}. Экономическая эффективность рассчитана проектным институтом, который учитывал расходы на строительство и эксплуатацию.

На эксплуатационные расходы мусороперегрузочной станции влияют цены на топливо (бензин) для транспортировки мусора, возможность выхода из строя мусоровывозящей техники, состояние автомобильных дорог от потребителя до полигонов, требования транспортной сети города и инфраструктура сложившихся транспортных потоков города и пригородных зон.

Большое число случайных факторов воздействуют на экономическую эффективность мини-завода с использованием пиролизной установки: цены на электроэнергию в регионе, автономная постановка электроэнергии (генераторы) в случае сбоя поставок электросети, большие затраты на строительство.

Экономическая эффективность мусоросжигательного завода будет зависеть от больших затрат на установку очистных сооружений, предотвращающих попадание в атмосферу выбросов, вредных для человека.

Таким образом, состояние обслуживающих механизмов в основном сказывается на расходах по эксплуатации мусороперегрузочной станции и мини-завода с использованием пиролизной установки. Следовательно, на эффективность мини-завода с использованием пиролизной установки будут влиять как состояние обслуживающих механизмов, так и цены на электроэнергию.

Случайные факторы, от которых зависит экономическая эффективность вариантов капиталовложений. Объединим в 4 возможных состояния с учётом окупаемости: Ω = (Θ_1, Θ_2, Θ₃ ,Θ₄):

Θ₁ ― цены (тарифы) на электроэнергию низкие и обслуживающие механизмы в хорошем состоянии;

Θ₂ ― цены (тарифы) на электроэнергию высокие и обслуживающие механизмы в хорошем состоянии;

Θ₃ ― цены (тарифы) на электроэнергию низкие и обслуживающие механизмы в плохом состоянии;

Θ₄ ― цены (тарифы) на электроэнергию высокие и обслуживающие механизмы в плохом состоянии.

Таблица 1.

Расчеты эффективности W (Θ_, a)

В стратегической игре (Ω, A, W) игрок 1 ― статистик, а игрок 2 ― природа. Матрица игры имеет седловую точку, равную 32 единицам:

Если бы не было дополнительной статистической информации, то на этом игра закончилась бы решением a₃ ― строить мусоросжигательный завод (это было бы осторожным решением).

Имеется ряд критериев, которые используются при выборе оптимальной стратегии.

1.  Критерий Вальда. Рекомендуется применять максиминную стратегию, т. е. выбирать худший из возможных вариантов (критерий основан на гипотезе крайнего пессимизма). Стратегия выбирается из условия a_ij= max {20,24,32}=32. Выбираем третью стратегию: строительство мусоросжигательного завода.

2.  Критерий максимума. Он выбирается из условия

= max {40,46,32}=46. Выбираем вторую стратегию: строительство мини-завода с использованием пиролизной установки .

3.  Критерий Гурвица. Критерий рекомендует стратегию, определяемую по формуле

, где наихудший вариант реализуется с вероятностью α (обычно принимается равным 0,5), а наилучший ― с вероятностью 1- α. В решаемой нами задаче:

max {0,5*20+0,5*40;0,5*24+0,5*46;0,5*32+0,5*32}= max {30,35,32}=35. Выбираем вторую стратегию: строительство мини-завода с использованием пиролизной установки.

С помощью имеющихся временных рядов можно получить апостериорную информацию, поскольку о влиянии на цены за электроэнергию таких состояний, как выход обслуживающих механизмов из строя, износ составляющих обслуживающего оборудования и т. п., существует статистическая информация.

По данным множительной статистики цен получены оценки эмпирического распределения состояний обслуживающих механизмов:

P (Θ₁) = 0, 20

P (Θ₂) = 0, 35

P (Θ₃) = 0, 17

P (Θ₄) = 0, 28

Имея распределение состояний обслуживающих механизмов, можно преобразовать стратегическую игру (Ω, A, W) в статистическую, в которой платёж игроку (статистику) будет определён как математическое ожидание в данном распределении состояний природы M[W(Θ,a)].

Математическое ожидание максимизирует оптимальная байесовская стратегия статистика, что равнозначно минимизации байесовского риска в статистической игре, в которой функция потерь L(Θ,a) = -W(Θ,a).

Для отдельных решений получим математические ожидания M[W(Θ,a)]:

M[W(Θ,a₁)] = 40*0,2+20*0,35+38*0,17+22*0,28 = 27, 62

M[W(Θ,a₂)] = 46*0,2+40*0,35+24*0,17+30*0,28 = 35,68

M[W(Θ,a₃)] = 32*0,2+32*0,35+32*0,17+32*0,28 = 32

Вывод: оптимальным решением, по результатам, полученным при проверке критериев, будет инвестирование средств в проект a₂ ― строительство мини-завода с использованием пиролизной установки.

Список литературы:

1.           Экономико-математические методы модели под редакцией Макарова С.И. Москва 2009, с. 97―107

2.           Солодовников А.С., Бабайцев В.А. Математика в экономике учебник, Москва « Финансы и статистика» 2003 г.

3.           Дубров А.М, Лагоша Б.А., Хрусталев Е.Ю. Моделирование рисковых ситуаций в экономике и бизнесе