ИССЛЕДОВАНИЕ ИЗМЕНЕНИЯ ВЫПУСКА ПРОДУКЦИИ И ФОНДООТДАЧИ НА ОСНОВЕ ПРОИЗВОДСТВЕННЫХ ФУНКЦИЙ
Секция: 11. Экономика

VII Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: общественные и экономические науки»
ИССЛЕДОВАНИЕ ИЗМЕНЕНИЯ ВЫПУСКА ПРОДУКЦИИ И ФОНДООТДАЧИ НА ОСНОВЕ ПРОИЗВОДСТВЕННЫХ ФУНКЦИЙ
Производственной функцией называется зависимость выпуска производства y от затрат производственных ресурсов x1, x2, …, xn
Чаще всего производственная функция является показательно-степенной функцией вида ![]() 0 < a1, a2 < 1, которая называется функцией Кобба-Дугласа, где y — объем производства, x1 — затраты труда (рабочей силы) и x2 — основные производственные фонды.
0 < a1, a2 < 1, которая называется функцией Кобба-Дугласа, где y — объем производства, x1 — затраты труда (рабочей силы) и x2 — основные производственные фонды.
Эффективностью труда называется средний по труду продукт, и она равна
![]()
Предельной производительностью труда называется выражение
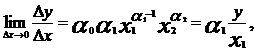
Она показывает число дополнительных единиц продукции при дополнительно затраченной единицы труда.
Эластичность выпуска по затратам труда равна
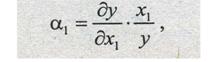
Производственная функция является математической моделью выпуска продукции и для экономического анализа этой функции применяются методы математического анализа.
Из наиболее распространенных производственных функций является функция Кобба-Дугласа: Y = AKaLβ , где A, α, β > 0 — константы, где α + β < 1; К — объем основных производственных фондов; L — объем трудовых ресурсов, т Y — выпуск продукции. Легко проверить, что выполняются требования к производственным функциям. ∂Y/∂K = AαKα-1Lβ > 0, ∂Y/∂L = AβKαLβ-1 > 0.
Вторые производные производственной функции: ∂Y2/∂K2 = Aα(α—1)Kα-2 Lβ < 0, ∂Y2/∂L2 = Aβ(β—1)KαLβ-2 > 0.Отсюда следует убывание предельных продуктов.
Для производственной функции Кобба-Дугласа средняя производительность труда y = Y/L =AKαLβ−1, и так как β < 1,то она убывает.
Предельная производительность труда ∂Y/∂L = AβKαLβ-1 > 0,следовательно, для функции Кобба-Дугласа предельная производительность труда пропорциональна средней производительности и меньше ее. Точно также устанавливается зависимость между средней и предельной фондоотдачей — предельная фондоотдача пропорциональна средней фондоотдаче и меньше ее.
Эластичность продукции по труду:
(∂Y/∂L):(Y/L) = (∂Y/∂L)L/Y = AβKαLβ-1 L/(AKαLβ) = β.
Эластичность продукции по труду показывает, объем трудовых ресурсов увеличить на β %, то выпуск продукции увеличится на 1 %. Аналогично, рассматривается экономический смысл параметра α (эластичности продукции по фондам).
На практике чаще всего рассматривается функция Кобба-Дугласа и при ее составлении иногда отказываются от некоторых условий .
Аналогично средней и предельной производительности труда вводится понятие фондоотдачи, которая характеризует эффективность использования основных фондов. Она рассчитывается как отношение объема выпуска продукции за единицу времени к полной стоимости основных производственных фондов.
Наилучшее использование основных производственных фондов нужно для увеличения выпуска общественного продукта и увеличения национального дохода.
Экономический эффект повышения использования основных фондов состоит в росте общественной производительности труда.
Фондоотдача показывает количество продукции (или прибыли) получаемой с каждого рубля основных производственных фондов.
Для повышения эффективности производства, важно, чтобы был обеспечен опережающий рост производства продукции по сравнению с ростом основных производственных фондов.
Рассмотрим составление производственной функции и ее изменение в зависимости от изменения переменных.
Допустим производство предприятия описывается функцией Кобба-Дугласа. Если один рабочий производит в единицу времени продукции на 100 тыс. р. Численность рабочих — 10 000 чел. Основные производственные фонды в денежном выражении оцениваются в 1 млрд. руб. Известно, при увеличении выпуска продукции на 6 % необходимо увеличить или стоимость основных фондов на 9 %, или число рабочих на 12 %. Функцию Кобба-Дугласа запишем в виде y=α0x1α1x2α2, где х1 — затраченный труд; х2 — капитал.
Найдем коэффициенты эластичности. Из условий х1=10 000 чел., х2=109 руб., находим объем продукции в стоимостном выражении у=х1×100 000=109 (руб.)
Применив логарифмическое дифференцирование, получим
Δу/у=α1Δх1/х1 +α2Δх2/х2,
где: Δу/у — изменение объема продукции;
Δх1/х1 — изменение трудовых ресурсов;
Δх2/х2 — изменение основных производственных фондов .
Известно Δу/у = 6 %, при этом, либо Δх2/х2 = 9 %, Δх1/х1 =0, либо, либо Δх1/х1 = 12 % , Δх2/х2 =0, то есть имеем два равенства 0,06=α1×0+α2×0,09; 0,06=α1×0,12+α2×0. Из этих уравнений находим α1=1/2; α2=2/3.
Подставляя полученные значения, получим у=α0х11/2х22/3
Отсюда α0=у/х11/2х22/3=109/![]() =10 000.
=10 000.
Итак, у=10 000х11/2х22/3. средняя производительность труда равна у/х1=109/104=105; предельная производительность труда — P![]() =α1
=α1![]() =
=![]() ×105=50 000.
×105=50 000.
Аналогично, определяем среднюю и предельную фондоотдачу:
![]() =109/109=1; P
=109/109=1; P![]() =α2
=α2![]() =
=![]() ×1=
×1=![]()
Исследуем изменение производственной функции у=3,2х10,4х20,6, где у — объем товарной продукции в стоимостном выражении, х1 — фонд заработной платы, х2 — стоимость основных фондов в зависимости от фонда заработной платы и основных производственных фондов. Допустим, произошло изменение используемых ресурсов: фонд заработной платы уменьшился на 6 %, а стоимость основных фондов возросла на 4 %. На сколько процентов при этом изменятся:
1. объем выпускаемой продукции,
2. производительность труда,
3. фондоотдача.
Для решения задачи применим метод логарифмического дифференцирования. ![]() =
= ![]() +0,4
+0,4![]() +0,6
+0,6![]() .,
.,
Тогда 
Величины ![]() ,
, ![]() , выражают относительные приращения величин х1 и х2, они соответственно равны –0,06 и 0,04. Тогда изменение объема товарной продукции
, выражают относительные приращения величин х1 и х2, они соответственно равны –0,06 и 0,04. Тогда изменение объема товарной продукции ![]() 0,4×(–0,06) + 0,6×0,04=0,024 — 0,024=0.
0,4×(–0,06) + 0,6×0,04=0,024 — 0,024=0.
Следовательно, объем товарной продукции не изменился. Производительность труда определяется равенством A![]() =
=![]() =3,2х1-0,6х20,6.
=3,2х1-0,6х20,6.
Логарифмируя это равенство, получим ![]() =
=![]() - 0,6
- 0,6![]() +0,6
+0,6![]() ;
;
![]() 0,6
0,6![]() – 0,6
– 0,6 ![]() =0,6
=0,6![]() 0,04–0,6×(–0,06)=0,024+0,036=0,06.
0,04–0,6×(–0,06)=0,024+0,036=0,06.
Таким образом, производительность труда выросла на 6 %.
Фондоотдача выражается формулой А![]() =
=![]() =3,2х10,4х2-0,4.
=3,2х10,4х2-0,4.
Логарифмируя это равенство, получим ![]() =
=![]() +0,4
+0,4![]() -0,4
-0,4![]() ,
,
![]() 0,4
0,4![]() - 0,4
- 0,4 ![]() =0,4
=0,4![]() (-0,06)-0,4×0,04=-0,04.
(-0,06)-0,4×0,04=-0,04.
Следовательно, фондоотдача снизилась на 4%
Список литературы:
- Уфимцева Л.И. Черкасова Т.Н. Математические модели некоторых стандартных задач в управлении предприятиями. Проблемы совершенствования организации производства и управления промышленными предприятиями. Межвузовский сборник научных трудов: выпуск 1, часть 2 Самара: изд-во СГЭУ, 2008 — 205—208 с.
- Экономико-математические методы и модели: Задачник учебно-практическое пособие под редакцией С.И. Макарова, С.А. Севастьяновой — М: Кнорус, 2009 — 208 с





