SWOT-АНАЛИЗ БАЛАНСОВЫХ МОДЕЛЕЙ
Секция: 11. Экономика

X Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: общественные и экономические науки»
SWOT-АНАЛИЗ БАЛАНСОВЫХ МОДЕЛЕЙ
За все годы существования экономической мысли величайшими учеными было создано множество различных теорий, систем и способов расчета. Некоторые из этих трудов пережили проверку временем, некоторые — нет, но некоторые, к сожалению, в наше время просто несправедливо забыты. В лучшем случае их изучают в ВУЗах при прохождении теоретических наработок в какой-то конкретной области, но и только. Так случилось и с моделью межотраслевого баланса В.В. Леонтьева, о которой ниже и пойдет речь.
Это теория была разработана В.В. Леонтьевым как действенный инструмент при анализе и прогнозировании структурных взаимосвязей в экономике. Она исходит из возможности достижения общего макроэкономического равновесия, для чего разработана модель этого состояния, включающая структурную взаимосвязь всех стадий производственного процесса — производства, распределения или обмена и конечного потребления.
На основе разработанных для США и некоторых других стран межотраслевых балансов В.В. Леонтьев анализировал состояние и структуру экономики, оценил возможные последствия структурной перестройки, разработал программу реструктуризации отраслей, рационализации транспортных сообщений и пр.
Межотраслевой баланс (метод «Затраты — выпуск») в международной трактовке — это разновидность балансовых построений, характеризующих межотраслевые связи, пропорции и структуру общественного производства. Он интегрируется в систему национальных счетов, конкретизирует основные счета СНС и позволяет отразить эффективность общественного производства, ценообразование, влияние факторов экономического роста и обеспечить прогнозирование процессов в экономике.
Таблица 1.
Рассмотрим модель межотраслевого баланса
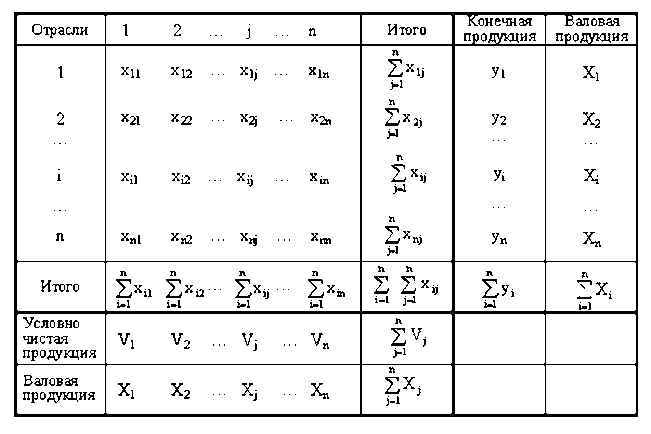
Предположим, что производственный сектор хозяйства разбит на n отраслей (энергетика, машиностроение, сельское хозяйство и т. д.).
Рассмотрим отрасль i, i = 1, 2,…, n. Она выпускает некую продукцию за данный промежуток времени (например, за год) в объеме xi, который еще называют валовым выпуском.
Часть объема продукции xi , произведенная i-ой отраслью используется для собственного производства в объеме xii , часть — поступает в остальные отрасли j = 1, 2,…, n для потребления при производстве в объемах xij , и некоторая часть объемом yi — для потребления в непроизводственной сфере, так называемый объем конечного потребления (личное потребление граждан, удовлетворение общественных потребностей, содержание государственных институтов и т. д.). Перечисленные сферы распределения валового продукта i-ой отрасли приводят к соотношению баланса
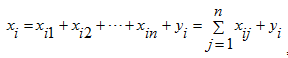 , i = 1, 2,…, n .
, i = 1, 2,…, n .
Т. к. продукция разных отраслей имеет разные измерения, то обычно под такими балансами понимаются стоимостные балансы.
Введем коэффициенты прямых затрат aij , которые показывают, сколько единиц продукции i-ой отрасли затрачивается на производство одной единицы продукции в отрасли j. Тогда можно записать, что количество продукции, произведенной в отрасли i в объеме xij и поступающей для производственных нужд в отрасль j, равно

Считаем сложившуюся технологию производства во всех отраслях неизменной (за рассматриваемый период времени), означающую, что коэффициенты прямых затрат aij постоянны. Тогда получаем следующее соотношение баланса, называемого моделью Леонтьева
 , i = 1, 2,…, n . (1)
, i = 1, 2,…, n . (1)
Введя вектор валового выпуска X, матрицу прямых затрат A и вектор конечного потребления Y
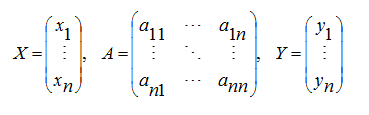
модель Леонтьева (1) можно записать в матричном виде
X = AX + Y (2)
Матрица A ≥ 0, у которой все элементы aij ≥ 0 (неотрицательны), называется продуктивной матрицей, если существует такой неотрицательный вектор X ≥ 0, для которого выполняется неравенство:
X > AX.
Это неравенство означает, что существует хотя бы один режим работы отраслей данной экономической системы, при котором продукции выпускается больше, чем затрачивается на ее производство. Другими словами, при этом режиме создается конечный (прибавочный) продукт Y = X – AX > 0.
Модель Леонтьева с продуктивной матрицей A называется продуктивной моделью.
Для проверки продуктивности матрицы A достаточно существования обратной матрицы B = (E – A)-1 с неотрицательными элементами, где матрица E — единичная матрица:
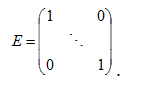 .
.
С помощью модели Леонтьева (2) можно выполнить три вида плановых расчетов, при условии соблюдения условия продуктивности матрицы A:
1. Зная (или задавая) объемы валовой продукции всех отраслей X можно определить объемы конечной продукции всех отраслей Y
Y = (E — A)X
2. Задавая величины конечной продукции всех отраслей Y можно определить величины валовой продукции каждой отрасли
X = (E — A)-1Y (3)
3. Задавая для ряда отраслей величины валовой продукции, а для всех остальных отраслей — объемы конечной продукции, можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых.
Матрица:
B = (E — A)-1
называется матрицей полных материальных затрат. Ее смысл следует из матричного равенства (3), которое можно записать в виде X = BY. Элементы матрицы B показывают, сколько всего необходимо произвести продукции в i-ой отрасли, для выпуска в сферу конечного потребления единицы продукции отрасли j.
История и практика баланса народного хозяйства в нашей стране послужила важной основой для составления межотраслевых балансов. Разработка межотраслевого баланса позднее стала органической частью системы национальных счетов (СНС).
На практике широко используется Международная стандартная классификация всех сфер экономической деятельности, в которой дана классификация всех отраслей национальной экономики. Она позволяет сформировать систему национальных счетов (СНС). Классификация и группировка по отраслям национальной экономики позволяют определить объемы и вклад конкретной отрасли в общий ВВП и ВНП, охарактеризовать связи между отраслями и сформированные пропорции. Сформированная функциональная группа позволяет провести объективный анализ роли хозяйствующих субъектов в производстве национального богатства.
Уход от использования только системы МОБ связан в первую очередь с такими его основными недостатками: 1) Опора на матрицу коэффициентов полных затрат приводит к трудоемкому процессу сбора и обработки большого объема статистической информации. Процесс производится с периодичностью 5 лет, что не дает полной картины динамики отрасли. 2) Нет учета технологических изменений в отраслях за период между сбором информации о матрице затрат. Это приводит к высокой стабильности коэффициентов, и следовательно, негибкости и неактуальности представляемых данных. Стабильность коэффициентов прямых материальных затрат (относительно стабильны).
Но если рассматривать Японию, как страну, которая до сих пор использует модель Леонтьева, то можно увидеть рост их экономики. Ниже представлены опубликованные министерством финансов этой страны данные.
Таблица 2.
Рост экономики Японии по данным министерства финансов
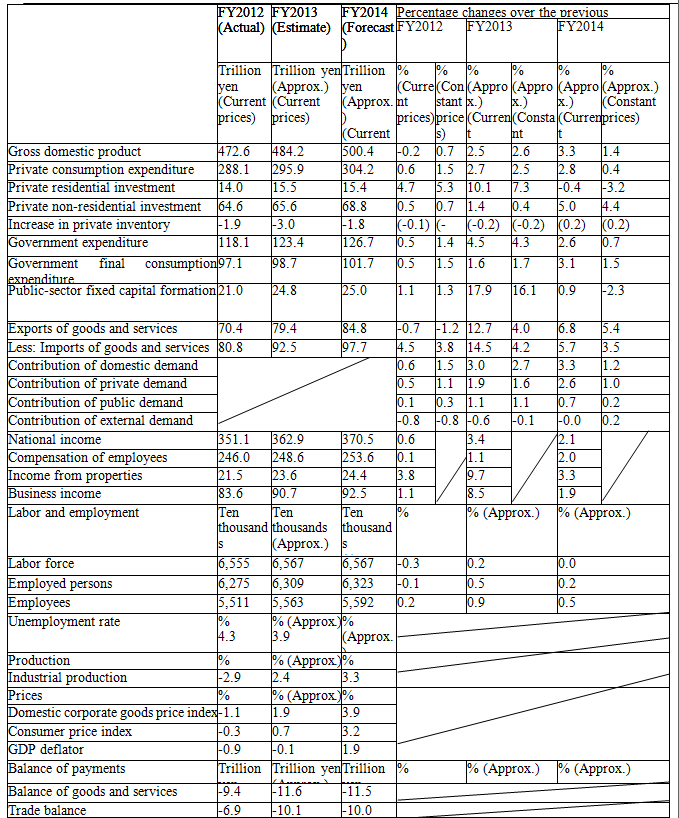
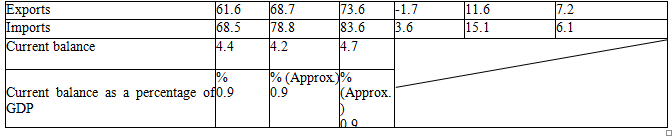
Итак, система межотраслевого баланса имеет огромное количество положительных сторон: она демонстрирует весь процесс воспроизводства, позволяет планировать отрасли системно с учетом места и веса каждой отрасли, дает возможность планирования на ряд лет, позволяя найти пути подъема как всей экономики страны, так и отдельных отраслей.
Однако не стоит забывать, что действительно необходим ряд улучшений, после применения, которых использование МОБ снова станет возможным, а именно: 1) даже на пике использования в нашей стране бралось в расчет до шестисот-семисот отраслей, в то время как Япония берет до двух тысяч. И этот способ оправдал себя. Экономика страны восходящего солнца находится на крайне высоком уровне. 2) система не является оптимальной из-за роста промышленного производства и прогресса в некоторых областях. Эту проблему можно решить двумя способами: первый — путем более частого составления матриц МОБ, второй — использование данных с учетом возможного изменения в будущем. 3)На данный момент система рассчитана только на отрасли материального производства. В связи с тем, что доля сферы услуг в экономиках многих стран неуклонно растет, является необходимым включение показателей этой отрасли в общий баланс. Данные возможно высчитывать на основе, применяемой в США системы подсчета удовлетворенности клиентов, приобретших ту или иную услугу.
Список литературы:
1. Экономико-математические методы и модели. Учебное пособие. / Р.И. Горбунова, С.И. Макаров, М.В. Мищенко, А.П. Сизиков, Л.И. Уфимцева, В.И. Фомин, Б.П. Чупрынов, Т.Н. Черкасова. / Под ред. С.И. Макарова — М-Кнорус, 2007. — 232 с.
2. Межотраслевой баланс Леонтьева и модели его расчёта. Энциклопедия экономиста. — [Электронный ресурс] — Режим доступа — URL: http: //www.grandars.ru/student/nac-ekonomika/mezhotraslevoy-balans.html (дата обращения 02.03.2014).
3. Межотраслевой баланс. Экономический портал. — [Электронный ресурс] — Режим доступа — URL: http://ecouniver.com/economik-rasdel/mikroekonomika-2/333-mezhotraslevoj-balans.html (дата обращения 03.03.2014).
4. Прямые затраты.FB.ru — [Электронный ресурс] — Режим доступа — URL: http: //fb.ru/article/39351/pryamyie-zatratyi (дата обращения 03.03.2014).
5. Материальные затраты предприятия. Центр управления финансами. — [Электронный ресурс] — Режим доступа — URL: http://www.center-yf.ru/data/economy/Materialnye-zatraty-predpriyatiya.php (дата обращения 04.03.2014).
6. Методологические проблемы разработки межотраслевого баланса. РГАУ-МСХА. — [Электронный ресурс] — Режим доступа — URL: http://www.activestudy.info/metodologicheskie-problemy-razrabotki-mezhotraslevogo-balansa (дата обращения 04.03.2014).





