НАХОЖДЕНИЕ ИЗМЕНЕНИЯ ИЗЛИШКА ПОТРЕБИТЕЛЯ В РЕЗУЛЬТАТЕ ПРОВЕДЕНИЯ ГОСУДАРСТВЕННОЙ ПОЛИТИКИ С ПОМОЩЬЮ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ

Математика и Экономика, на первый взгляд, абсолютно не совместимые науки, предметом изучение одной, из которых являются числа и связанные с ними измерения и подсчёты, а другой — производственные и хозяйственные отношения. То есть, по сути, абсолютно никак не соизмеримые и несвязанные вещи. Но на самом деле, на практике, эти две величайшие науки находятся в прочной взаимосвязи.

Начиная с 1738 года, после публикации Франсуаном Кенэ первых экономических таблиц, ученые пришли к выводу о том, что эти две науки, находясь во взаимодействии, способны с легкостью решать задачи, стоящие перед человеком.

Даже такой великий экономист, как Карл Маркс, при построении моделей простого и расширенного воспроизводства и денежного обращения использовал математический аппарат. А такие известные экономисты, как Вильфредо Парето, Леон Вальрас и Альфред Маршалл применяли математические методы в исследовании механизма функционирования рынка. И на сегодняшний день взаимодействие математики и экономики — абсолютно обычное явление.

В своей научной работе я бы хотела продемонстрировать, как с помощью такого математического метода, как интегральное исчисление, возможно исследовать процессы, происходящие в экономике.

Интегральное исчисление — огромнейший раздел математики, изучающий свойства и способы вычисления интегралов. Центральными понятиями интегрального исчисления являются понятия определённого и неопределенного интеграла.

При последующем рассмотрении экономический задач мною будет использоваться понятие определенного интеграла. Обозначают его так:

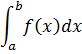
где:

∫ — знак интеграла;

a и b — соответственно нижний и верхний пределы интегрирования;

x — переменная интегрирования;

f(x)dx — подынтегральное выражение;

f(x) — подынтегральная функция.

Стоит вспомнить, что геометрический смысл определенного интеграла состоит в том, что определенный интеграл численно равен площади криволинейной трапеции.

Теперь мы можем приступить к практическим примерам использования интегрального исчисления в экономике. Начнем с такого понятия как потребительский излишек. Но прежде стоит ознакомиться с несколькими экономическими понятиями и обозначениями:

Спрос (D) — это обратная зависимость, устанавливаемая между ценой товара и объемом его покупки, сложившаяся на определенный момент времени. Графически спрос на товар изображают в виде кривой с отрицательным наклоном (Рис. 1), которая отражает взаимосвязь между ценой единицы товара — Р и количеством товара — Q, которое потребители готовы приобрести при заданной цене:

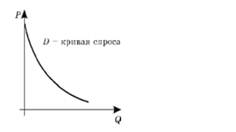
Рисунок 1. Кривая спроса

Противоположностью спроса на товар является предложение (S) — прямая зависимость между ценой товара и его количеством, предлагаемым к продаже. Предложение товара изображают графически в виде кривой с положительным наклоном (рис. 2):

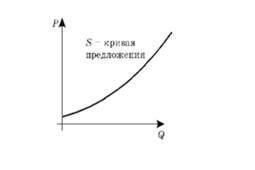
Рисунок 2. Кривая предложения

Также мы введем ещё одно понятие важное при моделировании экономических процессов, такое как рыночное равновесие (E). Это состояние возникает при такой цене и количестве товара, при которых объем спроса равен величине предложения. Графически рыночное равновесие изображают точкой пересечения кривой спроса и кривой предложения (рис. 3):

Рисунок 3. Рыночное равновесие

Теперь мы можем перейти к рассмотрению способа применения интегрального исчисления для определения потребительского излишка(CS) — разницы между ценой, которую потребитель готов заплатить за данный товар, и той, которую он реально платит. Для этого изобразим на графике обратную функцию спроса P = f(Q), в таком случае графически аргумент и значение функции будут изображаться более понятным для нас образом.

Допустим, покупатель приобретает товар в количестве Q* по равновесной цене P*. Общие расходы на его покупку составят P*Q*, а это равно площади фигуры A (рис.4):

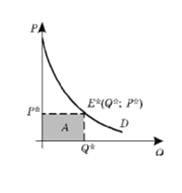
Рисунок 4. Расходы покупателя

Но предположим, что товар в количестве Q* реализуется продавцом не сразу, а поставляется на рынок постепенно, партиями — такое допущение является ключевым при вычислении потребительского излишка.

Площадь криволинейной трапеции B (рис. 5) равна сумме, которую потребитель готов отдать при покупке Q* единиц данного товара:

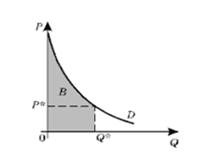
Рисунок 5. Сумма, которую потребитель готов отдать при покупке

Площадь фигуры В по данным рисунка 5 равна:

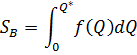
А разность между  и  и есть потребительский излишек (CS)(Рис. 6):

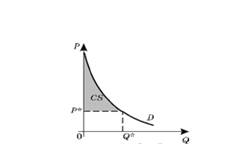
Рисунок 6. Потребительский излишек

Из этого следует, что его можно посчитать так:

CS =                                      (1)

Теперь рассмотрим применение формулы на конкретном примере:

Задача 1. Спрос на некоторый товар задается функцией, где за q принимается количество товара (в шт.), а за p — цена единицы товара (в руб.). Равновесие на рынке этого товара достигается при p* = q* = 2. Чему будет равна величина потребительского излишка?

Решение.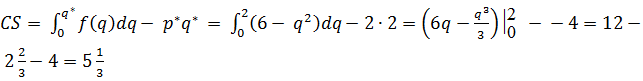

Ответ. Величина потребительского излишка  рублей.

Теперь перейдем к рассмотрению приложений интегрального анализа для определения излишка производителя (PS). Излишек производителя — разница между денежной суммой, за которую он был бы готов продать определенное количество товара, и той суммой, которую он действительно получит при его продаже. Графически он представляется площадью фигуры, ограниченной осью цен, прямой, параллельной оси абсцисс, проходящей через точку рыночного равновесия, и кривой предложения (рис. 7):

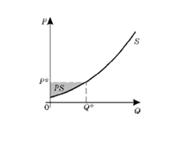
Рисунок 7. Излишек производителя

Очевидно, что:

PS =  —                           (2)

Рассмотрим, как полученная формула применяется при решении экономических задач:

Задача 2. Дана кривая предложения . Равновесие на рынке данного товара достигается при объеме продаж . Необходимо определить добавочную выгоду производителя при продаже такого количества продукции.

Решение. Для начала из функции предложения определим равновесное значение цены

Теперь подставим полученное значение в формулу (2):

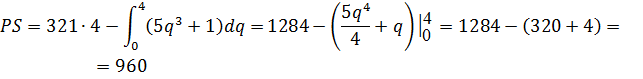
Ответ. Выгода производителя в данном случае 960 рублей.

Однако, в реальной жизни значения излишка потребителя и производителя представляют небольшой интерес для экономических деятелей. Для них более важно насколько изменится излишек потребителя в результате проведения государственной политики: при установлении налогов, введении субсидий и других меры, оказывающих влияние на равновесие на рынке.

Предположим, что единица товара облагается налогом в размере t (такой налог в среде экономистов называют «потоварным» налогом), тогда его цена увеличится с P1 до P2, где P2 = P1 + t (Рис. 8):

Рисунок 8. Изменение излишка потребителя

Итак, мы получаем, что  (уменьшение благосостояния потребителя) — есть разница площадей двух фигур и по форме напоминает криволинейную трапецию, площадь которой равна сумме площадей фигур и, то есть , где  (потери благосостояния потребителя, вследствие увеличения цены товара), а  (потери излишка потребителя, в связи с уменьшением количества потребляемого товара) равна:

 —  

Таким образом, изменение излишка потребителя в случае введения «потоварного» налога в размере t равно:

 = t +  -

Так же результат  в общем виде может быть найден так:

 =  +                       (3)

Теперь, воспользовавшись полученными формулами, мы можем оценить последствия введения «потоварного» налога на предложенном примере:

Задача 3. Известно, что спрос на некоторый товар имеет вид . Каков проигрыш потребителя при введении на некоторый товар налога с единицы продаж в размере 2 рублей, если известно, что изначально рыночное равновесие на данном рынке наблюдалось при цене  рубля?

Решение. Чтобы определить потребительские потери при увеличении равновесной цены с 3 рублей до 5 рублей, понаблюдаем, как при этом изменяется объем продаж. Если , то , при , то . Теперь, используя формулу (3), вычислим :

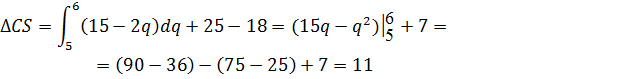
Ответ. Если «потоварный» налог будет введен, потребитель переплатит, приобретая данный товар, 11 рублей.

Список литературы:

1. Вечканова Г.Р., Вечканов Г.С. Микроэкономика, 8-е издание. Учеб. пособие. Изд.: «Питер», 2010. — 208 с.
2. Горбунова Р.И., Курганова М.В., Макаров С.И., Мищенко М.В., Нуйкина Е.Ю., Севастьянова С.А., Семенова М.М., Сергеева Л.В., Уфимцева Л.И., Фомин В.И., Черкасова Т.Н., Чупрынов Б.П. Математика для экономистов Задачник. Учеб.-практ. пособие / Под ред. Макарова С.И., Мищенко М.В.  М.: КНОРУС, 2008. — 360 с.
3. Макаров С.И. Математика для экономистов. Учеб. пособие / Под ред. С.И. Макарова.  М.: КНОРУС, 2008. — 264 с.
4. Паничева Л.В. Определенный интеграл при расчете экономической прибыли. / Современные наукоемкие технологии № 7, 2014.
5. Потоварный налог — [Электронный ресурс] — Режим доступа. — URL: http://www.ngpedia.ru/id174431p2.html (дата обращения 10.11.2014).