ОПТИМАЛЬНОЕ РАПРЕДЕЛЕНИЕ РЕСУРСОВ С ИСПОЛЬЗОВАНИЕМ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Секция: 11. Экономика

XIX Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: общественные и экономические науки»
ОПТИМАЛЬНОЕ РАПРЕДЕЛЕНИЕ РЕСУРСОВ С ИСПОЛЬЗОВАНИЕМ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Математика и Экономика — это самостоятельные области знаний, однако находящиеся в тесной взаимосвязи друг с другом. Их взаимодействие основано на исследовании экономических процессов и явлений с помощью построения математических моделей или, по-другому, упрощенных формальных описаний экономических систем. При их построении выявляются наиболее существенные факторы, необходимые для анализа, и отбрасываются детали, несущественные для решения поставленной задачи.
Использование математических методов позволяет достигнуть более полного изучения влияния отдельных факторов на общие экономические показатели деятельности организаций, уменьшить сроки осуществления анализа, повысить точность осуществления экономических расчетов, решить многомерные аналитические задачи, которые не могут быть выполнены традиционными методами, а также отобразить существующие связи в экономической жизни, оценить перспективы поведение экономических субъектов и экономическую динамику.
Одним из таких методов являются нахождение точек локального экстремума функции. Установим условия существования таких точек.
Если функция ![]() имеет в точке
имеет в точке ![]() локальный экстремум и частные производные первого порядка, то все эти частные производные равны нулю.
локальный экстремум и частные производные первого порядка, то все эти частные производные равны нулю.
В случае нескольких переменных необходимое условие существования локального экстремума имеет аналогичный вид — все частные производные первого порядка в точке ![]() должны обращаться в нуль.
должны обращаться в нуль.
При этом точки, в которых выполняются выше указанные условия, называются стационарными точками (точками возможного экстремума).
Достаточное условие существования локального экстремума можно сформулировать следующим образом. Допустим, что в точке ![]() возможного экстремума функции
возможного экстремума функции ![]() и в некоторой ее окрестности все вторые частные производные данной функции непрерывны. Тогда, обозначив за
и в некоторой ее окрестности все вторые частные производные данной функции непрерывны. Тогда, обозначив за ![]() ,
, ![]() ,
, ![]() вторые частные производные рассматриваемой функции
вторые частные производные рассматриваемой функции ![]() ,
, ![]() ,
, ![]() соответственно, получим: если
соответственно, получим: если ![]() , то функция
, то функция ![]() имеет в точке
имеет в точке ![]() локальный экстремум (минимум при
локальный экстремум (минимум при ![]() и максимум при
и максимум при ![]() ); если же
); если же ![]() , то данная функция в точке
, то данная функция в точке ![]() не имеет локального экстремума.
не имеет локального экстремума.
Перейдем к конкретным случаям практического применения функций нескольких переменных в экономических задачах.
Допустим, что ![]() — количество производимых n разновидностей товара, а их цены, соответственно —
— количество производимых n разновидностей товара, а их цены, соответственно — ![]() (все Рi — постоянные величины). Тогда затраты на производство этих товаров зададим функцией издержек
(все Рi — постоянные величины). Тогда затраты на производство этих товаров зададим функцией издержек ![]()
Функция издержек С(х) определяет затраты, необходимые для производства х единиц данного продукта.
Прибыль вычисляется по формуле: ![]() , где
, где ![]() — доход от производства х единиц продукта.
— доход от производства х единиц продукта.
Тогда функция прибыли будет иметь вид
![]()
Максимум прибыли найдем из необходимого условия локального экстремума функции нескольких переменных при ![]() :
:
![]() , при i = 1, 2, …, n
, при i = 1, 2, …, n
Получаем систему алгебраических уравнений относительно переменных хi
![]() , при i = 1, 2, …, n
, при i = 1, 2, …, n
Данная система уравнений отображает известное правило экономики: предельная стоимость (цена) товара равна предельным издержкам на производство этого товара. Решениями системы являются n-мерные точки.
Если производится два вида товаров, обозначим их количества через х и у. Пусть цены на эти товары будут равны Р1 = 8 и Р2 = 10 соответственно, а функция затрат С= х2+ ху + у2. Найдем максимум прибыли по формуле:
![]()
Из необходимого условия локального экстремума имеем систему алгебраических уравнений.
![]()
Решение этой системы является точка (2, 4).
Применяя достаточное условие существования экстремума, найдем дискриминант D = AC – B2.
Так как А = 2, В = 1, С = 2, то D = AC – B2 = 3, значит найденная точка определяет локальный максимум функции прибыли, равный Пmax = 28.
Теорию функции многих переменных можно применить при нахождении оптимального распределения ресурсов. Пусть функция выпуска имеет вид
![]() , а функция затрат на ресурсы x и y линейна, т. е.
, а функция затрат на ресурсы x и y линейна, т. е.
![]() , где Р1 и Р2 — соответствующие цены на эти факторы.
, где Р1 и Р2 — соответствующие цены на эти факторы.
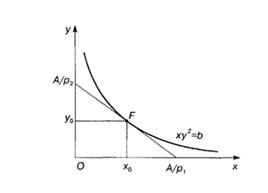
В точке оптимального распределения ресурсов F(x0, y0) линии функций выпуска и затрат касаются (Рис.1). На графике они определяются уравнениями:
![]() ,
, ![]() или
или 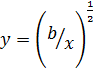 ,
, 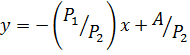 , где
, где ![]() и
и
![]() постоянные числа, а
постоянные числа, а ![]() .
.
Рисунок 1. График функции выпуска
Найдем координаты точки из уравнения:
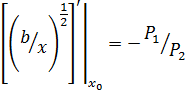
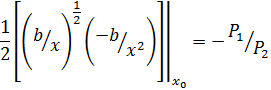
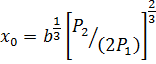
Определим значение y0 из уравнения линии уровня функции выпуска:
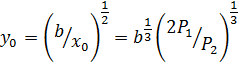
Отсюда получим, что оптимальное распределение ресурсов должно быть произведено в отношении P2: 2P1.
Список литературы:
- Горбунова Р.И., Курганова М.В., Макаров С.И., Мищенко М.В., Нуйкина Е.Ю., Севастьянова С.А., Семенова М.М., Сергеева Л.В., Уфимцева Л.И., Фомин В.И., Черкасова Т.Н., Чупрынов Б.П. Математика для экономистов. Задачник. Учеб.-практ. пособие / Под ред. Макарова С.И., Мищенко М.В. М.: КНОРУС, 2008. — 360 с.
- Горбунова Р.И., Курганова М.В., Макаров С.И., Мищенко М.В., Нуйкина Е.Ю., Севастьянова С.А., Сизиков А.П., Уфимцева Л.И., Фомин В.И., Чупрынов Б.П., Черкасова Т.Н. Экономико-математические методы и модели. Задачник. Учеб.-практ. Пособие / Под ред. Макарова С.И., Севастьяновой С.А. М.: КНОРУС, 2009. — 208 с.
- Уфимцева Л.И., Черкасова Т.Н. Возможности моделирования некоторых производственных процессов. Проблемы совершенствования организации производства и управления промышленными предприятиями. Межвузовский сборник научных трудов. — Самара: 2003. — 212—214 с.





