ИСПОЛЬЗОВАНИЕ МЕТОДА ОБРАТНОГО ПРЕОБРАЗОВАНИЯ ДЛЯ АНАЛИЗА ВРЕМЕННЫХ РЯДОВ
Секция: 11. Экономика

XXXIV Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: общественные и экономические науки»
ИСПОЛЬЗОВАНИЕ МЕТОДА ОБРАТНОГО ПРЕОБРАЗОВАНИЯ ДЛЯ АНАЛИЗА ВРЕМЕННЫХ РЯДОВ
Можно сказать, что для специалистов, занимающихся анализом данных, в большинстве случаев прогнозирование является основной целью и задачей. Современные методы статистического прогнозирования зачастую способны с достаточно высокой точностью спрогнозировать практически любые возможные показатели.
Прогнозирование – одна из форм предсказания, основанная на специальном научном исследовании, предметом которого являются вероятностно-возможные перспективы развития некоторого явления. Не существует универсальных методов прогнозирования на все случаи жизни, однако наиболее часто применяемым методом прогнозирования является математическое моделирование. Математическая модель – приближенное описание определенного процесса или явления внешнего мира, выраженное с помощью математического аппарата.
Часто при исследовании временного (динамического) ряда его изображают в виде следующей математической модели:
![]()
где: ![]() – значение временного ряда;
– значение временного ряда;
![]() – систематическая (детерминированная) составляющая временного ряда;
– систематическая (детерминированная) составляющая временного ряда;
![]() – случайная составляющая временного ряда.
– случайная составляющая временного ряда.
Систематическая составляющая временного ряда ![]() является результатом влияния на анализируемый процесс постоянно действующих факторов. Можно выделить две основные систематические составляющие временного ряда: тенденция и циклические колебания.
является результатом влияния на анализируемый процесс постоянно действующих факторов. Можно выделить две основные систематические составляющие временного ряда: тенденция и циклические колебания.
Тенденция (тренд), представляет собой общую закономерность изменения показателей временного ряда, устойчивую и наблюдаемую в течение длительного периода времени. Тренд описывается с помощью некоторой функции, как правило, монотонной. Эту функцию называют функцией тренда, или просто – трендом.
Среди факторов, формирующих цикличность колебаний ряда, в свою очередь можно выделить две компоненты: сезонность и цикличность. Сезонность представляет собой результат воздействия факторов, действующих с определенной, заранее известной периодичностью. Это регулярные колебания, носящие периодический характер и заканчиваются в течение года. Циклическая компонента – неслучайная функция, описывающая длительные (более года) периоды подъема и спада.
Случайная составляющая временного ряда ![]() – это оставшаяся после выделения систематических компонент составная часть временного ряда. Она отражает воздействие многочисленных факторов случайного характера и представляет собой случайную, нерегулярную компоненту.
– это оставшаяся после выделения систематических компонент составная часть временного ряда. Она отражает воздействие многочисленных факторов случайного характера и представляет собой случайную, нерегулярную компоненту.
Случайные величины разнообразны по своей природе, происхождению, однако закон распределения можно записать в единообразной универсальной форме, а именно в виде функции распределения, одинаково пригодной как для дискретных, так и для непрерывных случайных величин.
В целях прогнозирования, а также имитационного моделирования может возникнуть необходимость в методе генерации случайной компоненты временного ряда. Для этой цели воспользуемся методом обратного преобразования.
Пусть случайная величина, ![]() имеет функцию распределения
имеет функцию распределения ![]() . Примем, что
. Примем, что ![]() – это обратная функция
– это обратная функция ![]() . Тогда алгоритм для генерации случайной величины
. Тогда алгоритм для генерации случайной величины ![]() с функцией распределения
с функцией распределения ![]() будет следующим:
будет следующим:
1. Генерируем величину ![]() имеющую равномерное распределение на промежутке
имеющую равномерное распределение на промежутке ![]() ;
;
2. Возвращаем ![]() .
.
Рассмотрим наш временной ряд как последовательность ![]() независимых и одинаково распределенных, по определенному закону, случайных величин, которая называется выборкой объема
независимых и одинаково распределенных, по определенному закону, случайных величин, которая называется выборкой объема ![]() . Каждое
. Каждое ![]() называется вариантой. Имея выборку, мы не имеем информации о виде функции распределения
называется вариантой. Имея выборку, мы не имеем информации о виде функции распределения ![]() . Требуется построить оценку (приближение) для этой неизвестной функции.
. Требуется построить оценку (приближение) для этой неизвестной функции.
Наиболее предпочтительной оценкой функции ![]() будет являться эмпирическая функция распределения
будет являться эмпирическая функция распределения ![]() . Эмпирической функцией распределения называют функцию
. Эмпирической функцией распределения называют функцию ![]() , определяющую для каждого значения
, определяющую для каждого значения ![]() относительную частоту события
относительную частоту события ![]() , т.е.
, т.е.
![]() ,
,
где: ![]() – число значений
– число значений ![]() , меньших
, меньших ![]() ;
;
![]() – объем выборки.
– объем выборки.
При достаточно большом объеме выборки функции ![]() и
и ![]() мало отличаются друг от друга. Отличие эмпирической функции распределения от теоретической состоит в том, что теоретическая функция распределения определяет вероятность события
мало отличаются друг от друга. Отличие эмпирической функции распределения от теоретической состоит в том, что теоретическая функция распределения определяет вероятность события ![]() , а эмпирическая функция определяет относительную частоту этого же события.
, а эмпирическая функция определяет относительную частоту этого же события.
Однако для использования метода обратного преобразования удобно иметь непрерывную функцию распределения, поэтому необходимо интерполировать полученную эмпирическую функцию.
Приведем пример использования метода обратного преобразования при построении прогнозной модели. В качестве исходных данных используем среднемесячные показатели электропотребление на территории Красноярского края за 3 года с января 2009 г. по декабрь 2011 г. [2].
С помощью некоторой регрессионной модели были рассчитаны прогнозные значения временного ряда. Фактические ![]() и прогнозные
и прогнозные ![]() значения временного ряда представлены в таблице 1.
значения временного ряда представлены в таблице 1.
Таблица 1.
Фактические ![]() и прогнозные
и прогнозные ![]() значения временного ряда
значения временного ряда
|
t |
|
|
t |
|
|
t |
|
|
t |
|
|
|
1 |
51,01 |
53,09 |
11 |
35,58 |
43,42 |
21 |
37,86 |
44,58 |
31 |
17,14 |
15,15 |
|
2 |
38,23 |
38,37 |
12 |
53,25 |
54,26 |
22 |
63,49 |
57,61 |
32 |
20,85 |
21,45 |
|
3 |
40,00 |
35,24 |
13 |
52,38 |
52,69 |
23 |
72,98 |
72,28 |
33 |
29,37 |
31,55 |
|
4 |
25,13 |
32,13 |
14 |
39,91 |
41,30 |
24 |
88,02 |
83,09 |
34 |
51,17 |
44,09 |
|
5 |
22,93 |
27,08 |
15 |
39,21 |
32,14 |
25 |
82,60 |
79,01 |
35 |
61,58 |
59,79 |
|
6 |
27,01 |
20,64 |
16 |
31,34 |
24,38 |
26 |
62,72 |
63,15 |
36 |
71,25 |
73,02 |
|
7 |
25,11 |
17,77 |
17 |
26,01 |
19,52 |
27 |
50,02 |
48,20 |
|
|
|
|
8 |
16,69 |
19,20 |
18 |
20,55 |
17,87 |
28 |
29,62 |
34,02 |
|
|
|
|
9 |
27,31 |
23,86 |
19 |
12,12 |
22,62 |
29 |
22,29 |
22,75 |
|
|
|
|
10 |
29,24 |
31,48 |
20 |
24,93 |
32,44 |
30 |
17,80 |
15,25 |
|
|
|
Построим эмпирическую функцию распределения значений отклонений ![]() прогнозных значений
прогнозных значений ![]() от фактических значений
от фактических значений ![]() временного ряда (
временного ряда (![]() ). Для этого необходимо ранжировать выборку
). Для этого необходимо ранжировать выборку ![]() , таким образом, получив выборку
, таким образом, получив выборку ![]() (таблица 2).
(таблица 2).
Таблица 2.
Ряд значений ![]() и
и ![]()
|
t |
|
|
t |
|
|
t |
|
|
t |
|
|
|
1 |
-2,08 |
-10,50 |
11 |
-7,84 |
-2,08 |
21 |
-6,72 |
1,79 |
31 |
1,98 |
6,37 |
|
2 |
-0,14 |
-7,84 |
12 |
-1,00 |
-1,76 |
22 |
5,87 |
1,81 |
32 |
-0,59 |
6,48 |
|
3 |
4,75 |
-7,51 |
13 |
-0,30 |
-1,39 |
23 |
0,70 |
1,98 |
33 |
-2,17 |
6,96 |
|
4 |
-7,01 |
-7,01 |
14 |
-1,39 |
-1,00 |
24 |
4,92 |
2,55 |
34 |
7,07 |
7,06 |
|
5 |
-4,14 |
-6,72 |
15 |
7,06 |
-0,59 |
25 |
3,59 |
2,68 |
35 |
1,79 |
7,07 |
|
6 |
6,37 |
-4,40 |
16 |
6,96 |
-0,45 |
26 |
-0,42 |
3,44 |
36 |
-1,76 |
7,33 |
|
7 |
7,33 |
-4,14 |
17 |
6,48 |
-0,42 |
27 |
1,81 |
3,59 |
|
|
|
|
8 |
-2,50 |
-2,50 |
18 |
2,68 |
-0,30 |
28 |
-4,40 |
4,75 |
|
|
|
|
9 |
3,44 |
-2,25 |
19 |
-10,50 |
-0,14 |
29 |
-0,45 |
4,92 |
|
|
|
|
10 |
-2,25 |
-2,17 |
20 |
-7,51 |
0,70 |
30 |
2,55 |
5,87 |
|
|
|
Так как частота каждой вариации равна единице, эмпирическая функция будет иметь вид:
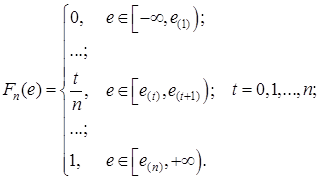
График функции ![]() представлен на рисунке 1.
представлен на рисунке 1.
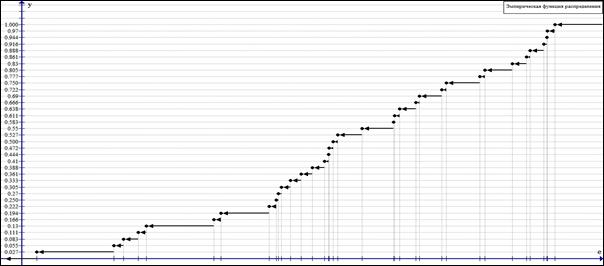
Рисунок 1. График эмпирическая функция распределения ![]()
Полученная эмпирическая функция ![]() имеет дискретный вид. Применим кусочно-линейную интерполяцию, чтобы получить непрерывную функцию распределения случайной величины
имеет дискретный вид. Применим кусочно-линейную интерполяцию, чтобы получить непрерывную функцию распределения случайной величины ![]() . Для этого используем уравнение прямой, проходящей через две точки:
. Для этого используем уравнение прямой, проходящей через две точки:
![]()
Непрерывная функция распределения случайной величины ![]() будет иметь вид:
будет иметь вид:
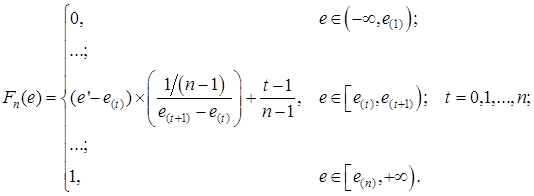
График функции ![]() представлен на рисунке 2.
представлен на рисунке 2.
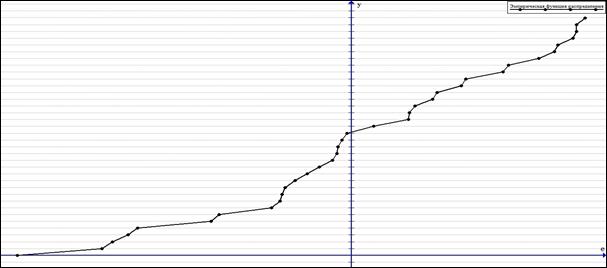
Рисунок 2. График непрерывной функции распределения ![]()
Для дальнейшего анализа данного метода, рассмотрим несколько моделей прогноза:
1. Значение временного ряда ![]() примем как полностью детерминированный процесс, для осуществления прогноза используем значения
примем как полностью детерминированный процесс, для осуществления прогноза используем значения ![]() , рассчитанные при помощи регрессионной модели;
, рассчитанные при помощи регрессионной модели;
2. Значение временного ряда ![]() примем как случайную величину, для которой построим функцию распределения
примем как случайную величину, для которой построим функцию распределения ![]() и осуществим расчет прогнозных значений
и осуществим расчет прогнозных значений ![]() ;
;
3. Значение временного ряда ![]() примем как совокупность значений
примем как совокупность значений ![]() , рассчитанных при помощи регрессионной модели и случайной компоненты
, рассчитанных при помощи регрессионной модели и случайной компоненты ![]() , для которой построим функцию распределения
, для которой построим функцию распределения ![]() и осуществим расчет прогнозных значений
и осуществим расчет прогнозных значений ![]() .
.
Сделаем оперативный прогноз уровней электропотребления. Для этого исключим из рассмотрения последние 5 наблюдений из выборки и рассчитаем новые оценки параметров регрессионной модели, а также новые функции распределения ![]() и
и ![]() .
.
Применим алгоритм обратного преобразования к полученным функциям ![]() и
и ![]() . Для этого сгенерируем выборку
. Для этого сгенерируем выборку ![]() случайных чисел, имеющих равномерное распределение в промежутке
случайных чисел, имеющих равномерное распределение в промежутке ![]() , и возвращаем
, и возвращаем ![]() и
и ![]() . Результаты расчета представлены в таблице 3.
. Результаты расчета представлены в таблице 3.
Таблица 3.
Результаты применения алгоритма обратного преобразования
|
№ |
t |
|
|
|
|
|
|
1 |
32 |
25,14 |
0,06 |
-7,13 |
18,01 |
6,97 |
|
2 |
33 |
37,16 |
0,65 |
1,96 |
39,13 |
14,93 |
|
3 |
34 |
52,03 |
0,65 |
2,10 |
54,14 |
15,25 |
|
4 |
35 |
70,54 |
0,05 |
-7,15 |
63,39 |
6,87 |
|
5 |
36 |
86,83 |
0,54 |
0,38 |
87,21 |
13,49 |
При рассмотрении полученных результатов видно, что сумма ![]() лежит ближе к фактическим данным, чем прогнозные значения
лежит ближе к фактическим данным, чем прогнозные значения ![]() , рассчитанные при помощи регрессионной модели. Таким образом, спрогнозированные значения
, рассчитанные при помощи регрессионной модели. Таким образом, спрогнозированные значения ![]() в некоторой степени сгладили ошибку прогноза
в некоторой степени сгладили ошибку прогноза
В качестве критерия оценки качества модели определим значение средней ошибки аппроксимации, которую рассчитаем по формуле:
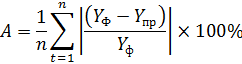
где: ![]() – прогнозные значение временного ряда;
– прогнозные значение временного ряда;
![]() – фактические значение временного ряда;
– фактические значение временного ряда;
n – размер временного ряда.
Значения средней ошибки аппроксимации составляют:
1) ![]()
2) ![]()
3) ![]()
Самый высокий показатель средней ошибки аппроксимации был получен при допущении, что временной ряд ![]() является случайной величиной. Средняя ошибка аппроксимации для регрессионной модели меньше на 54,15%, что говорит нам о том, что временной ряд является детерминированной величиной. В результате включения в регрессию значений
является случайной величиной. Средняя ошибка аппроксимации для регрессионной модели меньше на 54,15%, что говорит нам о том, что временной ряд является детерминированной величиной. В результате включения в регрессию значений ![]() , средняя ошибка аппроксимации снизилась еще примерно на 1,44%.
, средняя ошибка аппроксимации снизилась еще примерно на 1,44%.
Представленный выше метод может быть использован для определения непрерывной функции распределения случайной величины и генерации случайной величины в целях прогнозирования и имитационного моделирования.





