Структурная модель прогнозирования угроз информационной безопасности на основе временного ряда

Аннотация. Временные ряды имеют различные характеристики, для разных временных рядов применяются определенные методы прогнозирования. Для прогнозирования угроз информационной безопасности в данной статье будет описана специальная методика, включающая в себя прогнозирование с использованием базовой функции, которая будет распознаваться в исследуемом временном ряду, а затем экстраполироваться на будущие значения с помощью определенных методов прогнозирования.

Ключевые слова: временной ряд, регрессионная модель, сглаживание, метод скользящего среднего, коэффициент парной корреляции, аппроксимация функции, метод наименьших квадратов, аппроксимация функции, экстраполяция временного ряда.

Прогнозирование угроз информационной безопасности имеет особенности, которые необходимо учитывать, для того, чтобы прогноз был верен. К таким особенностям относится:

Высокая скорость изменения количества угроз определенных типов;

Связанность угроз друг с другом;

Отсутствие сезонности для временных рядов такого типа.

На основе данных особенностей можно сделать вывод, что точность прогноза должна быть высокой, а также, тренд должен быть явно выявлен, так как от направленности тренда зависит принятия решения. Кроме того, из-за связанности угроз, необходимо, чтобы прогноз производился одновременно для всех угроз.

На основе всего выше сказанного, было принято решение разработки модели прогнозирования, которая бы включала в себя полный цикл действий применяющийся для прогноза, начиная с распознавания образа и заканчивая получение прогнозных значений временного ряда.

Временной ряд – собранный в разные моменты времени статистический материал о значении каких-либо параметров исследуемого процесса.

Так как исходные данные будут представлены временным рядом, то мы заранее учитываем, что у нас имеются статистические данные по исследуемой угрозе.

Итак, выделим требования к модели, которые должны выполнятся для прогнозирования угроз информационной безопасности на основе временных рядов. Данные требования составлены с учетом особенностей прогнозирования угроз информационной безопасности:

1. Сглаживание выбросов и шума;

2. Наиболее быстрое выполнение прогноза;

3. Оптимальная точность;

4. На основе исходного временного ряда модель должна определять базовую функцию на основе базового временного ряда с соответствующей функцией;

5. Аппроксимация на основе базовой функции (нахождение параметров функции) близким к базовой.

6. Экстраполяция (прогноз) – продолжение ряда событий за известный диапазон. Учитывая особенности данного временного ряда, достаточным будет прогноз не дальше краткосрочного.

Все методы, используемые для анализа – в нашем случае будет использоваться для определения образа, и прогнозирования делят на две большие группы: статические модели и структурные модели. Классификация представлена на рисунке 1. [1]

Рисунок 1. Классификация методов и моделей прогнозирования

Серым цветом выделены модели, которые будут использоваться для разработки текущей модели, так как они подходят под требования прогнозирования угроз информационной безопасности.

Модель прогнозирования, которая будет представлена далее, будет базироваться на нескольких методах, рассмотренных выше, основной будет регрессионная модель. Кроме того, шаги, входящие в структурную модель, будут содержать математические элементы необходимые для решения конечной задачи. Основой структурной модели будет алгоритм, включающий элементы, которые позволят выполнять все необходимые требования, обозначенные ранее. Итак, для решения поставленной задачи будем использовать следующую последовательность этапов:

1. Сбор данных по заранее определенным угрозам – получение количества атак в единицу времени;

2. Сглаживание исходного ряда с помощью метода скользящего среднего;

3. Определение базовой функции с помощью коэффициента парной корреляции;

4. Аппроксимация функции – нахождение приблизительны числовых значений коэффициентов с помощью метода наименьших квадратов;

5. Экстраполяция временного ряда – продолжение во вне искомого временного ряда, прогноз данного ряда с помощью регрессионного анализа;

Каждый шаг данного алгоритма необходимо описать подробнее, затем будет составлена непосредственно структурная модель с учетом данного алгоритма.

1 При сборе данных вся собранная информация будет представлена в табличном виде по осям x и y, где x – момент времени в сек., а y – значение параметра. Пример вида угрозы информационной безопасности в виде временного ряда представлен в таблице 1.

Таблица 1

Отображение угрозы информационной безопасности в виде временного ряда

Отображение угрозы из таблицы 2 представлено на рисунке 2.

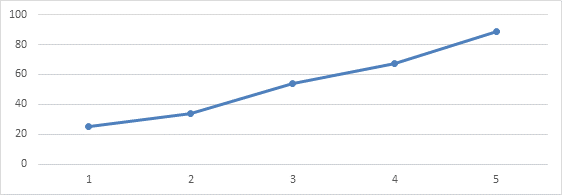
Рисунок 2. Количество атак угрозы информационной безопасности

Как видно по рисунку, данный временной ряда имеет все предпосылки прогнозирования (ярко выраженный тренд).

2 Сглаживание исходного ряда будет реализовываться с помощью метода простого скользящего среднего, так как это наиболее быстрый способ сгладить ряд при небольшом интервале сглаживания. Простое скользящее среднее является одним из наиболее широко используемых индикаторов в техническом анализе. Он не только используется в качестве самостоятельной методики, но и лежит в основе многих других технических индикаторов. При осуществлении сглаживания всем наблюдениям случайной величины из интервала сглаживания присваивается одинаковый удельный вес. С математической точки зрения простое скользящее среднее представляет собой среднее арифметическое значение, а для расчета его значения используется следующая формула: [2]

                                                                                                (1)

где SMA_t – значение скользящего среднего в период времени t;

n – интервал сглаживания;

P_t-i – значение случайной величины на момент (t-i).

Рассмотрим порядок сглаживания при помощи простого скользящего среднего на примере случайных данных, представленных в таблице 2.

Таблица 2

Пример сглаживания методом скользящего среднего

Предположим, что интервал сглаживания равен 2. В этом случае первое значение SMA может быть рассчитано для 2-го периода по приведенной выше формуле и составит 29,5.

SMA₂ = (25+35)/2 = 29.5

В третьем периоде его значение уже составит 44.

SMA₃ = (35+54)/2 = 44

Для следующих периодов расчеты были проведены аналогично и графически представлены на рисунке 3.

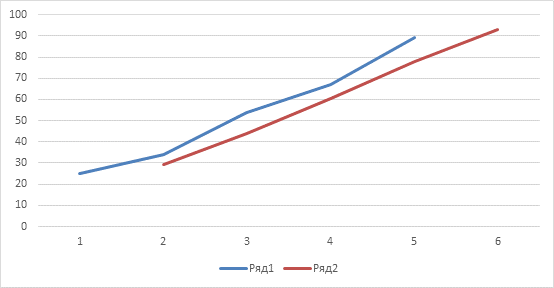
Рисунок 3. Сглаживание ряда скользящим средним

Рассмотренная методика технического анализа позволяет устранить резкие е колебания и установить направление превалирующего тренда.

3 Для того, чтобы прогноз был корректен, необходимо определить образ какой исходной функции похож на функцию временного ряда, которую необходимо прогнозировать. Для этого было принято решение использовать метод парной корреляции, суть которого определить коэффициент похожести функции в базе с коэффициентом функции исходного временного ряда. Необходимо отметить, что изначально в базе будут определенные функции для сравнения. Базовые функции представлены в таблице 3.

Таблица 3

Базовые функции

Базовые функции будут построены в среде MS Excel и их табличные значения будут сравниваться с табличными значениями угрозы информационной безопасности с помощью метода парной корреляции. То есть, с помощью корреляционного анализа можно установить какой график обладает наибольшей похожестью.

Можно измерить, как близко находятся наблюдения к прямой линии, которая лучше всего описывает их линейное соотношение путем вычисления коэффициента корреляции Пирсона

Его истинная величина в популяции (генеральный коэффициент корреляции) оценивается в выборке как r (выборочный коэффициент корреляции), которую обычно получают в результатах компьютерного расчета.

Пусть (x₁. y₁), (x₂, y₂),…,(x_n, y_n) - выборка из n наблюдений пары переменных (X, Y). [3]

Выборочный коэффициент корреляции r определяется как:

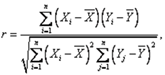                                                                                                                 (2)

Где  ̅x, ̅y - выборочные средние, определяющиеся следующим образом:

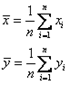
Корреляция для исходного примера равна 0.991863819.

4 Аппроксимация функции - функции f(x) называется нахождение такой функции (аппроксимирующей функции) g(x), которая была бы близка заданной. Критерии близости функций могут быть различные. Грубо говоря, аппроксимация позволит найти коэффициенты a и b в функции, что позволит сделать прогноз по найденному графику. Для нахождения параметров функции F, будем использовать метод наименьших квадратов, так как впоследствии будет использоваться регрессионный анализ для экстраполяции функции, основой которой является метод наименьших квадратов. [4]

5 Экстраполяция временного ряда – распространение тенденций, установленных в прошлом, на будущий период.

Прогноз временного ряда будет осуществляется с помощью регрессии, потому что данный метод имеет высокую скорость, что является ключевым в его выборе. Функции, используемые при экстраполяции, будут основываться на базовых, но с найденными коэффициентами. [5]

В результате, была разработана упрощенная структурная модель этапов работы, данная модель представлена на рисунке 4.

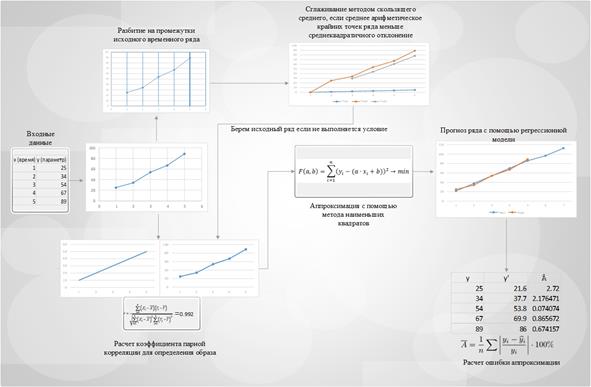
Рисунок 4. Структурная модель прогнозирования угроз ИБ