ИСПОЛЬЗОВАНИЕ ГЕНЕТИЧЕСКОГО АЛГОРИТМА ДЛЯ ФОРМИРОВАНИЯ ИНДИВИДУАЛЬНОГО МАРШРУТА ОБУЧЕНИЯ

Контроль знаний — одна из актуальных проблем современного профессионального образования. Несмотря на большое количество публикаций по этой проблеме, к вопросам, которые недостаточно проработаны, можно отнести контроль и оценку уровня сформированности профессиональной компетентности студента в процессе обучения в вузе.

Анализ научной литературы позволил выделить основные методы и алгоритмы компьютерного контроля знаний:

·     метод Раша, данная модель достаточно проста, по сравнению с другими, она характеризуется наименьшим числом параметров — только один параметр уровня знаний для каждого испытуемого и только один параметр трудности для каждого задания;

·     модель адаптивного тестового контроля предполагает использовать следующий подход. Если тестируемый решил задание, то у него появляется желание решить более сложное задание, в противном случае им будет сделана еще одна попытка решения задания той же сложности. Если оно также не решено, то предъявляется задача пониженной сложности. Таким образом, функция «уровня знаний» является преобразованием функции «сложности» задачи через «способность решения задач» определенной «сложности» [1];

·     абсолютная временная шкала измерения знаний. Метод изучает возможности «абсолютной временной шкалы оценивания знаний». При использовании абсолютной шкалы данного подхода существует возможность ответить на вопросы: 1) существует ли предел, к которому сходится итоговая оценка с увеличением времени тестирования (или количества заданий); 2) какова погрешность «измерения знаний» если прервать тестирование в некоторый определенный момент, например через 40 минут [2].

Таким образом, существует большое число методов, посвященных различным аспектам контроля знаний и основанных на современных достижениях науки и компьютерной техники. В то же время, одной из актуальных проблем остается формирование набора заданий, адекватно оценивающих уровень сформированности профессиональных компетенций студента. Обзор наиболее известных систем, широко используемых в современном дистанционном обучении, таких как BlackBoard, Desire2Learn, Moodle, WebCT, Sakai, показал, что, как правило, учебный курс представляет собой набор статических гипертекстовых документов. Все студенты получают одинаковый материал для изучения и сходные задания контроля приобретенных знаний, умений и навыков без учета их индивидуальных особенностей. Наиболее востребованным видом компьютерного контроля, нашедшим применение в оценке знаний и умений студентов, является компьютерное тестирование. При всех положительных моментах компьютерного тестирования, этот метод не позволяет в полной мере оценить все заявленные образовательных стандартах компетенции.

Учитывая вышесказанное, отметим, что методика проведения контроля в условиях компетентностно-ориентированной образовательной программы:

·     должна быть максимально гибкой, учитывающей индивидуальные способности и профессиональные интересы студента;

·     должна давать возможность студенту выбора индивидуального обучающего маршрута на основе имеющегося у него личностного и профессионального опыта.

Под индивидуальным маршрутом обучения мы будем понимать выбираемую студентом в соответствии с требованиями рабочей программы дисциплины, а также с учетом личных и профессиональных интересов последовательность учебных заданий, в результате выполнения которых, студентом приобретаются новые или развиваются ранее приобретенные профессиональные компетенции и при этом достигаются цели изучения дисциплины.

Задача построения индивидуального маршрута обучения сводится к выбору последовательности обучающих заданий, которая отвечает следующим условиям:

·     общая временная протяженность. Общее время, которое потребуется затратить на выполнение заданий;

·     минимальный ранг задания. Определяет минимальный ранг, который должно иметь задание для включения в маршрут.

Для различных вариантов маршрутов обучения необходимо ввести критерии сравнения:

·     коэффициент удовлетворения потребностей;

·     среднее значение ранга;

Под индивидуальным маршрутом обучения будем понимать вектор

,

где:  — кортеж признаков, характеризующий обучающее задание.

,

где: No — порядковый номер задания, соответствующий строке матрицы преемственности заданий С,

d — порядковый номер задания, соответствующий столбцу матрицы потребности N (d = 0, если задание не является обязательным),

s — признак завершенности задания,

z — время, необходимое для выполнения задания студентом,

r — ранг задания.

Условимся для обозначения отдельного признака задания использовать запись , где sim — символ некоторого признака, а k — порядковый номер задания в векторе T. С учетом введенных обозначений дадим определения указанных критериев.

Коэффициент удовлетворения потребностей — величина, характеризующая степень удовлетворения потребностей в части выбора базовых образовательных единиц, формирующих заданный набор компетенций. Для вычисления данного показателя применяется следующая формула:

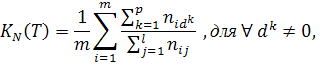
где:n_ij — элемент матрицы потребностей N,

m — число строк в матрице N,

l — число столбцов в матрице N,

p — число базовых заданий в перечне T,

Среднее значение ранга индивидуального маршрута определяется по формуле:

где:m — число заданий, входящих в перечень T,

 — ранг задания

Общая временная протяженность вычисляются только для заданий, которые не содержат признак завершенности. Для нахождения данных показателей необходимо воспользоваться формулами:

,

где: V — общая временная протяженность изучения маршрута,

m — число заданий в маршруте, не содержащих признака изученности,

zⁱ — время, необходимое для освоения .

В соответствии с перечисленными ограничениями и критериями сравнения лучшим вариантом перечня дидактических единиц будет считаться тот, для которого выполняются следующие условия:

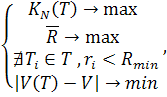
где: V — общая временная протяженность, заданная преподавателем.

Таким образом, задача формирования оптимального перечня дидактических единиц, способствующего развитию заданных компетенций, является сложной многокритериальной задачей, кроме того, заранее не известен размер исследуемого набора заданий. Для поставленной задачи предлагается использовать механизм генетических алгоритмов (ГА).

Генетические алгоритмы предназначены для решения задач оптимизации. ГА работают с совокупностью особей — популяцией, каждая из которых представляет возможное решение данной проблемы. Каждая особь оценивается мерой ее приспособленности согласно тому, насколько хорошо соответствующее ей решение задачи. Наиболее приспособленные особи получают возможность воспроизводить потомство с помощью перекрестного скрещивания с другими особями популяции. Наименее приспособленные особи с меньшей вероятностью смогут воспроизвести потомков. Иногда происходят мутации, или спонтанные изменения в генах. Таким образом, из поколения в поколение, хорошие характеристики распространяются по всей популяции. Скрещивание наиболее приспособленных особей приводит к тому, что исследуются наиболее перспективные участки пространства поиска. В конечном итоге популяция будет сходиться к оптимальному решению задачи.

Под популяцией будем понимать конечное множество вариантов перечней образовательных компонентов. В соответствии с введенными ранее обозначениями популяция описывается совокупностью:

,

где: n — численность популяции.

Особи, входящие в популяцию, в генетических алгоритмах, представляются хромосомами, с закодированными в них множествами параметров задачи. В терминах рассматриваемой задачи особями являются варианты маршрутов заданий Tⁱ. Каждый перечень Tⁱ характеризуется определенным составом заданий, который выступает в роли интересующего нас параметра. Таким образом, каждая особь кодируется единственной хромосомой. В роли генов будем рассматривать только те задания, которые находятся в непосредственной связи с компетенциями, входящими в исследуемый набор.

Совокупность хромосом особи представляют собой генотип. В свою очередь, набор значений, т. е. декодированная структура, соответствующая генотипу называется фенотип. В качестве фенотипа выступает структура:

,

где: p — число заданий, входящих в перечень .

Для представления генотипа предлагается использовать двоичное кодирование хромосомы особи.

Для оценки каждой особи в популяции необходимо задать функцию приспособленности. Поскольку решаемая задача является многокритериальной, то и функций приспособленности будет несколько:

В этом случае необходимо найти некоторый компромисс, в роли которого выступает решение, оптимальное в смысле Парето. Для нахождения такого компромисса воспользуемся подходом, предложенным в работе [4, 167 с.]. Согласно данному подходу особь, являющаяся лидером в данной популяции, определяется по формуле:

,

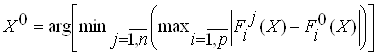где: n — численность популяции,

p — количество оптимизируемых функций,

 — значение i-ой функции приспособленности для j-ой особи,

–наилучшее значение i-ой функции среди всех особей популяции.

Таким образом, лучшей будет та особь популяции, которая имеет наименьшее среди наибольшего отклонения от лучшего значения функций приспособленности в популяции.

Поскольку мы имеет дело с критериями, имеющими различную размерность, то имеет смысл перейти к безразмерным критериям. Для этого в рассматриваемом подходе предлагается воспользоваться следующей формулой:

,

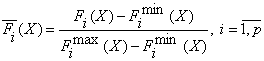где:  и  — соответственно наименьшее и наибольшее значения i-ой функции приспособленности в популяции.

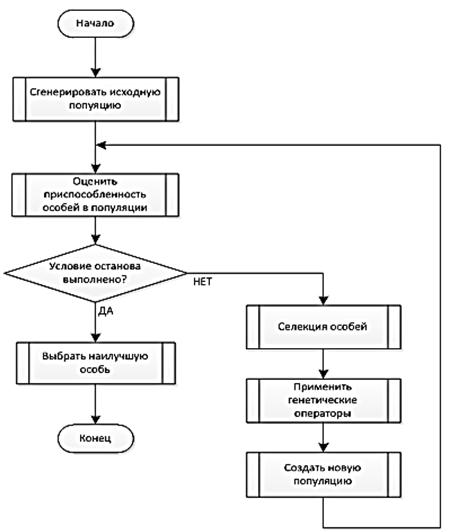
Рисунок 1. Схема работы генетического алгоритма

Когда задача сформулирована в терминах генетического алгоритма, можно приступить к его реализации. Схема работы ГА приведена на рисунке 1.

Результатом работы описанного алгоритма является перечень образовательных компонентов, оптимальный (с точностью, необходимой для поддержки принятия решения) с точки зрения заданных ограничений.

Таким образом, используемый алгоритм призван повысить качество подготовленности студентов, формировать и улучшать навыки студента, за счет адаптивного формирования набора заданий. Реализация методик обучения студентов на основе индивидуальных маршрутов обучения способствует: развитию профессиональной самостоятельности студентов, повышению профессионального интереса и индивидуализации обучения.

Список литературы:

1.            Алексахин С.В., Николаев А.Б., Строганов В.Ю. Модели адаптивного тестового контроля в системе дистанционного образования // Информационные технологии в образовании. — 2001. — № 6. [электронный ресурс] — Режим доступа. — URL: http://ito.edu.ru/2001/ito/VI/VI-0-17.html (дата обращения 3.02.2013).

2.            Зайцева Л.В., Прокофьева Н.О. Проблемы компьютерного контроля знаний // Proceedings. IEEE International Conference on Advanced Learning Technjlogies (ICALT 2002). 9—12 September 2002/ Kazan, Tatarstan, Russia, 2002. — P. 102—106.

3.            Крылов Ю.Н. Абсолютная временная шкала измерения знаний. Динамика результатов тестирования во времени// Информационные технологии в образовании. — 2001. — № 6. [электронный ресурс] — Режим доступа. — URL: http://ito.su/2001/ito/VI/VI-0-32.html (дата обращения 12.10.2012).

4.            Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы: Пер. с польск. И.Д. Рудинского. — М.: Горячая линия — Телеком, 2006. — 452 c.