ПРОДОЛЬНЫЙ КОЭФФИЦИЕНТ РАСПРОСТРАНЕНИЯ И ОПРЕДЕЛИТЬ ЕГО КРИТИЧЕСКУЮ ЧАСТОТУ.
Секция: 13. Радиотехника, Электроника

IV Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
ПРОДОЛЬНЫЙ КОЭФФИЦИЕНТ РАСПРОСТРАНЕНИЯ И ОПРЕДЕЛИТЬ ЕГО КРИТИЧЕСКУЮ ЧАСТОТУ.
В статье дается краткое описание параметров скорости передачи информации по ВОЛС. Рассматриваются методы продольного коэффициента, чтобы иметь критическую частоту. Используя их рассчитывание и значения функцию Бесселя, построен график симметричных и несимметричных волн.
Введение
Темпы роста производства волоконной оптики и оптических кабелей за рубежом опережают темпы производства электрических кабелей и составляют 40 % в год. Ряд стран уже сейчас отказался от традиционных металлических кабелей и строительство новых линии связи переводит на оптические кабели. В мире идет интенсивный процесс совершенствования как оптических кабелей, так и оптоэлектронной аппаратуры. Получают широкое развитие оптические кабели с одномодовыми волокнами, осваиваются новые диапазоны инфракрасного диапазона и новые материалы с малыми потерями. Добавляя к этому, сейчас важная цель в мире это — повышение скорости передачи информации. Недавно в РФ намечали, что скорость передачи информации увеличивать до 10 Тбит/с в 2020 г.
Продольный коэффициент распространения β является важнейшим параметром, определяющим форму сигнала,качество и скорость передачи по линии.На основании ранее приведенных волновых уравнений и используя значения поперечных коэффициентов ![]() (для сердцевины) и
(для сердцевины) и ![]() (для оболочки) , получаем следующее выражение для расчета β(рад/км):
(для оболочки) , получаем следующее выражение для расчета β(рад/км):
![]() , (1)
, (1)
где: ![]() и
и ![]() — показатели преломления сердцевины и оболочки;
— показатели преломления сердцевины и оболочки;
![]() — расчетная частота;
— расчетная частота;
![]() — критическая частота;
— критическая частота;
![]() — скорость света;
— скорость света;
![]() — диаметр сердцевины;
— диаметр сердцевины;
![]() — волновое число;
— волновое число;
![]() — угловая частота.
— угловая частота.
 , (2)
, (2)
где ![]() — значение корней функций Бесселя для различных типов волн (см. табл. 1);
— значение корней функций Бесселя для различных типов волн (см. табл. 1);
![]() — скорость света;
— скорость света;
![]() — диаметр сердцевины;
— диаметр сердцевины;
![]() и
и ![]() — показатели преломления сердцевины и оболочки
— показатели преломления сердцевины и оболочки
Таблица 1.
Значения корней функции Бесселя
n |
значение |
Тип волны |
||
1 |
2 |
3 |
|
|
0 |
2,405 |
5,520 |
8,654 |
|
1 |
0,000 |
3,832 |
7,016 |
|
1 |
3,832 |
7,016 |
10,173 |
|
2 |
2,445 |
5,538 |
8,665 |
|
2 |
5,136 |
8,417 |
11,620 |
|
при ![]() продольная коэффициент для оболочки выражается так
продольная коэффициент для оболочки выражается так
![]() , (3)
, (3)
где:![]() — волновое число для оболочки;
— волновое число для оболочки;
![]() — скорость света;
— скорость света;
![]() показатели преломления сердцевины и оболочки;
показатели преломления сердцевины и оболочки;
![]() — угловая частота
— угловая частота
при ![]() продольная коэффициент для сердцевины
продольная коэффициент для сердцевины
![]() , (4)
, (4)
где:![]() — показатели преломления сердцевины;
— показатели преломления сердцевины;
![]() — угловая частота;
— угловая частота;
![]() — скорость света
— скорость света
![]() , (5)
, (5)
где: ![]() — волоновое число;
— волоновое число;
![]() — длина волны;
— длина волны;
![]() — фазовая скорость;
— фазовая скорость;
![]() — угловая частота
— угловая частота
Теперь сравнить формулу, который связано со скорости
![]() , (6)
, (6)
значить ![]() .
.
Из рисунок 1 где приведена частотная зависимость коэффициента распространения, видно, что β изменяется от значений ![]() в оболочке (при
в оболочке (при ![]() )до значений
)до значений ![]() в сердцевине (при
в сердцевине (при ![]() ), т. е
), т. е ![]() .[1]
.[1]
Для каждого моды имеется своя критическая частота. Волна ![]() не имеет критической частоты.
не имеет критической частоты.
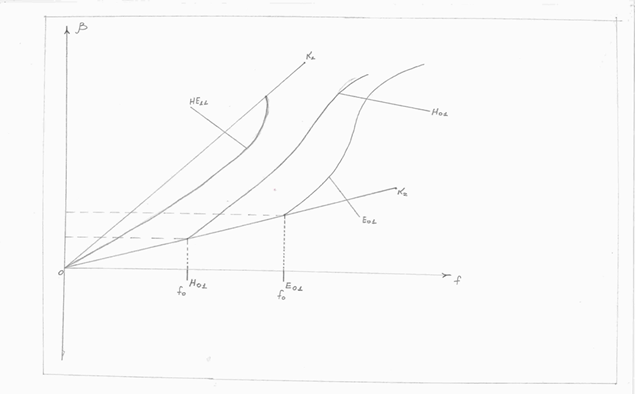
Рисунок 1. Частотная зависимость коэффициента распространения
Мы можем определить по следующим выражением, имеет ли продольная частота критическую частоту. Поэтому (1) формулу надо преобразовать и получаем следующую[2]
![]() , (7)
, (7)
![]() (8)
(8)
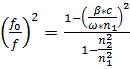 (9)
(9)
![]() , (10)
, (10)
![]() , (11)
, (11)
Теперь сравнить с (2)
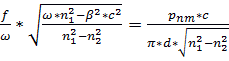 , (12)
, (12)
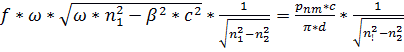 , (13)
, (13)
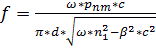 , (14)
, (14)
Дальше β равно
![]() , (15)
, (15)
![]() , (16)
, (16)
Теперь построим график из таблицы (2)
Таблица 2.
Диаметр сердцевины для различных типов волн ![]()
|
Критическая частота, |
||||
8 |
10 |
40 |
50 |
100 |
|
2,405 |
18,4 |
14,7 |
3,32 |
2,66 |
1,33 |
3,83 |
26,8 |
21,1 |
5,29 |
4,23 |
2,12 |

Рисунок 2. Частотная зависимость коэффициента распространения
Из рисунок 2 приведен графический результат коэффициента распространения. Рассматривая зависимость коэффициента мы можем сказать, что он симметричный и имеет критическую область.
Заключение
Из рисунок 2, где показан ход кривых, видно, что с ростом частоты Н несколько растет. Наша цель была определить критическую частоту и мы выяснили, в этом случае волна симметричная.
Список литературы:
1. Гроднев И.И., Мурадян А.Г., Шарафутдинов Р.М., Алексеев Е.Б., Александровский М.И., Сванидзе Р.Г., Ксенофонтов С.Н., Хабибуллин В.М. Волоконно-оптические системы передачи и кабели / Справочник — М.: Радио и связь, 1993 — 264 с.
2. [Электронный ресурс] — Режим доступа. — URL: www.science.direct.com





