МОДЕЛИРОВАНИЕ НАДЕЖНОСТИ УЗЛОВ РЕМОНТНО — ТЕХНОЛОГИЧЕСКОГО ОБОРУДОВАНИЯ ПО ИЗМЕНЕНИЮ ТОЧНОСТИ НАСТРОЙКИ
Секция: 8. Машиностроение

IX Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
МОДЕЛИРОВАНИЕ НАДЕЖНОСТИ УЗЛОВ РЕМОНТНО — ТЕХНОЛОГИЧЕСКОГО ОБОРУДОВАНИЯ ПО ИЗМЕНЕНИЮ ТОЧНОСТИ НАСТРОЙКИ
Процесс изменения показателя точности является случайным и описывается посредством случайных величин, характеризующих скорость его отклонения от задаваемого настройкой ремонтно-технологического оборудования (РТО), а также неслучайных функций, выражающих зависимость настроечного параметра U от времени t.
Изменение показателя U(t) определяется с помощью схемы, изображенной на рисунке 1. При u ≥ 1 имеет место отказ, предупреждение или устранение которого осуществляется очередной подналадкой.
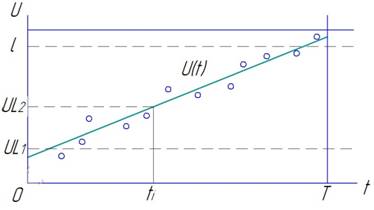
Рисунок 1. Закон распределения, определяющий вероятность выхода показателя U за его предельную границу
Формирование закона распределения j(U), определяющего вероятность выхода показателя U за его предельную границу, т. е. вероятность отказа, происходит в соответствии со схемой на рисунке 2.
Плотность распределения наработки до отказа определяется на основе теоремы о преобразовании случайных величин. Так как величина U является случайной, с плотностью распределения j(U), то с помощью данной теоремы можно определить распределение наработки j(t). Очевидно, что вероятность попадания случайной величины Ui на элементарный отрезок dU равна вероятности попадания ti на dt, выражаемые формулой
 (1)
(1)

Рисунок 2. Схема формирования отказов РТО
Тогда плотность распределения случайно величины U(t) принимает положительные значения, определяемые по формуле:
 (2)
(2)
где Y(t) — функция, обратная заданной функции.
Рассмотрим функцию изменения показателя точности [2], имеющую вид U(t)=U0+Vct, и при условии, что U0 не является случайной величиной. При фиксированном предельном отклонении Un=1 и известной величине Vc наработка РТО определяется t=(1-U0)/Vc, а при известной наработке Т скорость изменения показателя точности, являясь обратной функцией, выражается Vc=(1-U0)/T. Средний ресурс РТО можно выразить как mt=(1-U0)/mv, где mv — среднее значение скорости изменения U(t), а среднее значение изменения показателя точности в момент времени Т равно mu=U0+mvT.
Учитывая вышеизложенное и используя выражение (2) определим искомую функцию:
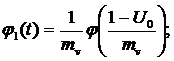 (3)
(3)
При нормальном законе распределения ресурса РТО плотность распределения равна:
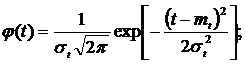 (4)
(4)
где σt — среднее квадратическое отклонение ресурса.
Тогда плотность распределения U в любой фиксированный момент времени t определяется
 (5)
(5)
или при нелинейном протекании процесса
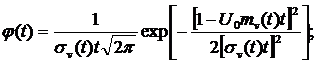 (6)
(6)
где σv — среднее квадратическое отклонение показателя U в момент времени t.
Рассмотрим общую схему формирования отказов при изменении показателя точности. Вначале, как правило, имеет место известное рассеивание параметров настройки РТО, выражаемое распределением j(U0) относительно своего математического ожидания m0 со среднеквадратическим отклонением σ0. При определенных условиях начальной настройки, рассеяние U0 с некоторой вероятностью может выходить за границу поля допуска, тогда возможна вероятность брака в начальной период работы РТО. Хотя в дальнейшем, при возрастании U(t) данный отказ имеет тенденцию к самоустранению, следует учитывать, что вероятный брак здесь может являться неисправимым при выполнении множества операций механической обработки, так как происходит больший съем материала с обрабатываемой заготовки.
В начальный период работы происходит также приработка РТО, учитываемая в моделях величиной DU и имеющая распределение j(DU) с параметрами Dm и σD .
Для отыскания закона распределения j(t) для функции двух и более переменных имеются общие вероятностные зависимости, аналогичные формуле (1). Как правило, их непосредственное применение приводит к громоздким преобразованиям, так как возникает необходимость брать двойной интеграл по некоторой области.
Однако, если случайные аргументы U0, Du, Uc и Uz распределены по нормальным законам, то показатель U для каждого значения t=T будет распределен по тому же закону со следующими параметрами:
математическое ожидание
![]() (7)
(7)
среднее квадратическое отклонение
![]() (8)
(8)
здесь σ0, σD, σv, σz является средними квадратическими отклонениями соответствующих составляющих U0, Du, Vc, Uz входящих в функцию U(t) изменения показателя точности.
Надежность РТО, характеризуемая успешным выполнением задания и вероятностью безотказности, численно равна площади кривой распределения j(U), заключенной в пределах от 0 до 1 в заданный момент времени t, что определяется интегрированием [1]
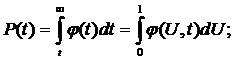 (9)
(9)
В случае закона нормального распределения (ЗНР) выражение имеет вид
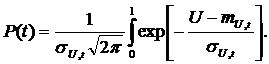 (10)
(10)
На практике имеет место множество известных вариантов реализаций отклонений уровня настройки РТО во времени.
Используя выражения (6)—(10), и выразив P(t) через нормированную функцию Лапласа, получим следующие выражения.
1. Значение P(t) в начальное время работы ТС определяется:
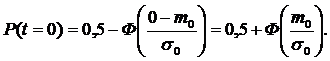 (11)
(11)
Через время Т=tпод значение P(t) соответствует выражению
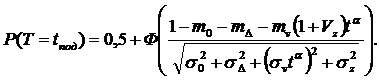 (12)
(12)
2. В начальный момент работы РТО величина P(t=0)=0, так как проведенная настройка исключает в данный момент выход формируемого параметра за допускаемые пределы. Это связано с особенностью формирования мгновенного поля рассеяния получаемых параметров при его расширении в направлениях двух пределов. Тогда через определенное время T=tпод величина P(T) соответствует выражению
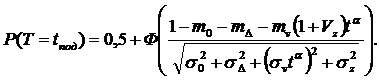 (13)
(13)
С помощью выражений (10)—(12) определяется значение P(t) в заданный момент времени, так как рассматриваются мгновенные распределения j(U).
В результате проведенных исследований выявлено, что все другие варианты реализации отклонений уровня настройки РТО во времени, описываемые разработанными моделями являются частными случаями рассмотренных. Поэтому, при рассмотрении различных вариантов изменение показателя точности, следует исходить из формул (11) и (12) в результате их упрощения.
Список литературы:
- Мартышкин А.П. Формирование надежности операционного размерного контроля при механической обработке/ Лезин П.П. и др. // Организационные, философские и технические проблемы современных машиностроительных производств //Сборник материалов, часть 1. Изд-во Мордовского университета, 2000. — С. 91—93.
- Фигуроки Я.О прогнозировании групповых предупредительных замен элементов с учетом их наработки // Надежность и контроль качества. 1982. № 4. С. 57—59.





