ИССЛЕДОВАНИЕ ФУНКЦИЙ СРЕДСТВАМИ МАТЕМАТИЧЕСКОЙ СИСТЕМЫ MathCAD
Секция: 3. Информационные технологии

VI Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
ИССЛЕДОВАНИЕ ФУНКЦИЙ СРЕДСТВАМИ МАТЕМАТИЧЕСКОЙ СИСТЕМЫ MathCAD
В очень широком круге задач, связанных с моделированием окружающего мира, требуются достаточно серьезные знания из различных разделов математики, некоторые из которых принято относить к области высшей математики. Удобным и эффективным средством решения подобных математических задач являются специализированные математические пакеты. Математика является естественной областью приложений информатики и важнейшим звеном, связывающим информатику с другими науками. Пакет MathCAD, в отличие от других математических приложений, построен в соответствии с принципом «Что Вы видите, то и получите». Поэтому он очень прост в использовании, в частности, из-за отсутствия сначала писать программу, реализующую те или иные математические расчеты, а потом запускать на исполнение. В состав системы MathCAD входят несколько интегрированных компонентов: мощный текстовый редактор, позволяющий вводить и редактировать текст и математические выражения; вычислительный процессор, умеющий проводить расчеты по введенным формулам, используя встроенные численные методы; символьный процессор, являющийся, фактически, системой искусственного интеллекта; огромное хранилище справочной информации, как математической, так и инженерной, оформленной в качестве интерактивной электронной книги.
Исследование функций различной степени сложности и построение их графиков является важнейшей задачей математического анализа. В основе изучения поведения функций лежит вычисление производных, пределов, решение уравнений и неравенств, нахождение асимптот, а с подобными операциями MathCAD справляется весьма эффективно. Благодаря графическим возможностям системы можно построить график функции любой сложности — он наглядно отразит особенности ее поведения и значительно упростит проведение исследования.
Поскольку алгоритм исследования функции включает в себя большое количество пунктов, разберем каждый из них по отдельности на примере:
Пример. ![]()
1. При исследовании функции в пакете MathCAD все символьные расчеты необходимо сопоставлять с графиком. Для облегчения поставленной задачи построим в первую очередь график функции. Заметьте, что при проведении исследования на бумаге такой возможности у вас нет.
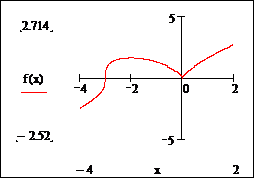
Рисунок 1. График функции ![]()
2. Найдем область определения функции
Из математики нам известно, что совокупность значений х, для которых данная функция определена, называется областью определения этой функции. Так как в выражении функции отсутствуют корни четной степени и знаменатель, то х может принимать любые значения (-∞;∞), поэтому функция определена на всей числовой оси.
3. Область значений функции принадлежит (-∞;∞)

4. Определим, является ли функция четной или нечетной
Функция называется четной, если выполняется условие f(-x)=f(x), и нечетной, если f(-x)=-f(x). График четной функции симметричен относительно оси Y, нечетной — начала координат. По графику функции видно, что он несимметричен относительно оси ординат и начала координат, значит, это функция общего вида. Подтвердим это вычислением:

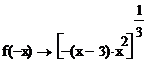

Из полученных выражений видно, что условия четности и нечетности не соблюдаются, значит, это функция общего вида.
5. Определим, является ли функция периодической или непериодической.
Функция называется периодической, если для любого х существует такое действительное число Т, отличное от нуля, что f(x+T)=f(x).
Доказательством периодичности / непериодичности функции является нахождение величины Т из уравнения f(x+T)=f(x). Если Т является действительным числом, функция периодична. В случае непериодичности Т будет являться функцией от х.
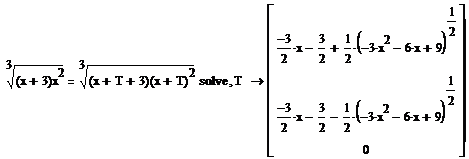
При решении уравнения мы получили три значения. По определению Т≠0, остальные же выражения зависят от х, следовательно, функция является непериодической.
6. Точек разрыва функция не имеет, поскольку непрерывна на промежутке (-∞;∞).
7. Найдем точки пересечения графика функции с осями координат:

График функции пересекает ось Х в точках (-3;0), (0;0)
![]()
График функции пересекает ось Y в точке (0;0)
8. Определим точки экстремума функции.
Точки минимума и максимума функции называются точками экстремума.
· Необходимым условием существования экстремума в точке является равенство нулю или равенство бесконечности производной в данной точке.
· Достаточным условием существования экстремума в точке является смена знака производной при переходе через данную точку:
- если производная меняет знак с плюса на минус, то это максимум
- если производная меняет знак с минуса на плюс, то это минимум
Найдем производную функции f(x)
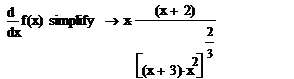
Приравняем производную нулю и решим уравнение относительно переменной х.
![]()
Производная равна нулю при х=-2, при х=-3 и х=0 она обращается в бесконечность. Значит, данные критические точки являются точками экстремума.
Чтобы проверить достаточное условие, найдем интервалы возрастания и убывания функции. Для этого решим следующие неравенства:

![]()
Во-избежании ошибки при решении неравенств в MathCAD результат следует проверить по графику. С помощью графика мы можем указать корректные промежутки знакопостоянства исследуемой функции: в интервале![]() функция возрастает и в интервале
функция возрастает и в интервале![]() убывает.
убывает.
При переходе через точку х=-2 производная меняет знак с + на —, значит, в данной точке функция имеет максимум:
![]()
При переходе через точку х=0 производная меняет знак с — на +, значит, в данной точке расположен минимум:
![]()
При х=-3 экстремума нет, поскольку знак производной сохраняется.
9. Найдем асимптоты графика функции в виде y=kx+b
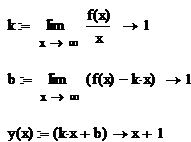
Получили прямую y(x)=x+1, которая является наклонной асимптотой. Отразим ее на графике исследуемой функции. Видно, что расстояние от асимптоты до точек графика функции неограниченно уменьшается с ростом х.
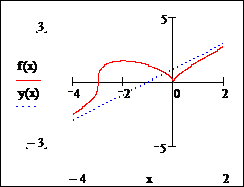
Рисунок 2. Асимптота графика функции ![]()
Большинство этапов исследования в MathCAD нам пришлось проводить, используя классические формулы и определения, что благоприятно сказывается на актуализации математической подготовки.
Список литературы:
1. Гурский Д. Вычисления в MathCAD. — Мн.: Новое знание, 2003. — 395 с.
2. Гурский Д., Турбина Е. MathCAD для студентов и школьников. Популярный самоучитель. — СПб.: Питер, 2005. — 400 с.
3. Дьяконов В.П., Абраменкова И.В. MathCAD 8 PRO в математике, физике и Internet. — М.: Нолидж, 2000. — 512 с.
4. Кудрявцев Е.М. MathCAD 11: Полное руководство по русской версии. — М.: ДМК Пресс, 2005. — 592 с.





