О ДИФФЕРЕНЦИАЛЬНОМ МОДЕЛИРОВАНИИ ЗАКОНА ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ

Для изучения реальных процессов с большим успехом используются математические модели.

Под математической моделью реального процесса в общем случае понимается приближенное описание этого процесса на языке математики. Искусство математического моделирования состоит в умении перевести техническую задачу на математический язык.

В данной статье рассматривается дифференциальное моделирование реальных процессов, на примере закона изменения температуры. Для достижения поставленной цели в рамках данной статьи подвергнем разбору дифференциальные уравнения в следующих задачах практического содержания.

Задача 1.

Котел вместимостью 1 м³ первоначально наполнен водой, имеющей температуру 100º С. По верхней трубе начинает поступать вода, температура которой равна 40º С, одновременно по нижней трубе вода вытекает из котла. За каждую минуту втекает 200 литров. Найти закон изменения температуры в котле (как функции от времени). Предполагается, что вода в котле постоянно перемешивается, так что в любой момент времени её температура во всех точках внутри котла одна и та же. Определить, через какой промежуток времени температура воды в котле понизится до50º.

Пусть Q(t) — количество теплоты (в килокалориях), которое содержится в воде, наполняющей котел в момент времени t, тогда температура воды равна Q(t)/1000. В начальный момент (при t = 0) имеем Q(0) = 1000×100 = 10⁵. Рассмотрим некоторое значение t. За последующее время t в котел прибывает количество теплоты, равное 200t×40 (время t измеряем в минутах), и уходит количество теплоты, равное 200/1000×Q(t)t. Следовательно, получаем равенство

Откуда после деления обеих частей на t имеем:

В пределе при t→0 это равенство примет вид

 Получили дифференциальное уравнение с разделяющимися переменными:

Решая это уравнение, последовательно находим:

Начальное условие Q(0) = 100000 даёт 100000 = С + 40000, т. е. С = 60000. Итак, окончательно получим

Отсюда находим температуру воды в котле как функцию от t:

Обозначая через tο промежуток времени, за который температура понизится до 50º, можем записать 50 = 40 + 60 е, т. е. е = 1/6, откуда tο= 8,96 мин.

Задача 2.

Михаил и Владимир заказали в кафе кофе и сливки. Когда им одновременно подали по чашке одинаково горячего кофе и сливки, они поступили следующим образом. Михаил добавил в кофе немного сливок, накрыл чашку бумажной салфеткой и вышел позвонить по телефону. Владимир сразу же накрыл чашку бумажной салфеткой, и добавил то же количество сливок только через 10 минут, когда вернулся Михаил, и они начали пить кофе вместе. Кто же пил более горячий кофе?

Данная задача решается с учетом естественных предположений, которые отражают физическое содержание происходящих процессов, и заключается в следующем. Будем считать, что теплообмен через поверхность стола и салфетки намного меньше теплообмена через боковые стенки чашек; температура пара в чашке над поверхностью жидкости равна температуре жидкости.

Сначала рассмотрим динамику изменения температуры кофе в чашке Владимира до смешивания кофе со сливками и выведем соответствующее дифференциальное уравнение.

Количество теплоты, в соответствии с принятыми допущениями, полученное воздухом от чашки Владимира, определяется соотношением

                                                             (1)

где: Т — температура кофе в момент времени t,

θ — температура воздуха в кафе;

ŋ — теплопроводность материала чашки;

l — толщина стенок чашки;

s — площадь боковой поверхности стенок чашки.

С другой стороны, количество теплоты, отданное кофе, определяется из следующего соотношения

dQ = — cmdT,                                                            (2)

где: с — удельная теплоемкость кофе;

m— масса кофе в чашке.

Приравнивая правые части уравнений (1) и (2), получим:

Если разделить переменные, то последнее выражение можно переписать в виде:

                                                            (3)

Обозначим начальную температуру кофе через Тο и проинтегрируем дифференциальное уравнение (3). Таким образом, получим аналитическое описание закона, по которому изменялась температура кофе в чашке Владимира до смешивания кофе со сливками.

                                             (4)

Теперь рассмотрим закон изменения температуры кофе после того, как Владимир добавил в чашку сливки. Для этого необходимо уравнение теплового баланса, которое в нашем случае запишется в виде:

                                   (5)

где: θв — температура смеси в момент времени t;

T1 — температура сливок;

c1 — удельная теплоемкость сливок;

m1 — масса сливок, добавленная в кофе.

Данное уравнение теплового баланса позволяет нам получить соотношение для нахождения температуры смеси, которое выглядит следующим образом:

                                      (6)

С учетом равенства (4), полученную формулу можно переписать в виде

                      (7)

Последняя формула задает закон изменения температуры кофе после добавления в чашку Владимира сливок.

Далее будем рассматривать динамику изменения температуры кофе в чашке Михаила. С этой целью снова воспользуемся уравнением теплового баланса, которое в данном случае принимает вид

                                   (8)

где: θ0  — температура смеси.

Данное уравнение позволяет нам записать соотношение для нахождения температуры смеси в чашке Михаила.

Снова воспользуемся уравнением (4), где роль начальной температуры играет уже θ0, а произведение cm заменяется суммой cm + c1m1. Таким образом, закон изменения температуры θм кофе в чашке Михаила аналитически задается формулой:

                (9)

Проведем численные расчеты для определения температуры кофе Михаила и Владимира, имея в виду, что с1 ≈ 3,9 ×10³ Дж/(кг×К), с ≈ 4,1 × 10³ Дж/(кг×К), ŋ ≈ 0,6 В/(м×К), и полагая для определенности m1 = 2 × 10ˉ² кг, m = 8 × 10ˉ² кг, Т1 = 20° С, θ = 20°С, Тo= 80 °C, s = 11*ˉ³ м ², l = 2*10ˉ³ м. Вычисления показывают, что наиболее горячий кофе пил Михаил.

Задача 3.

Температура вынутого из печи хлеба в течение 20 минут падает от 100° C до 60° C. Температура воздуха 25° C. Через сколько времени от момента начала охлаждения температура хлеба понизится до 30° C? Учесть, что скорости охлаждения тела пропорциональна разности температуры тела и окружающей среды.

Для решения поставленной задачи введем некоторые обозначения и определим условия.

Искомая величина y — температура хлеба в момент времени t.

Начальные условия: t = 0, y(0) = 100.

Дополнительные условия: t=20, y(20) = 60.

Рассмотрим температуру хлеба как функцию от времени: y=y(t).

Скорость охлаждения — это скорость изменения данной функции: .

По условию задачи: , где kl = 25, k<0.

Обозначим: t=0,

 , .

Решим полученное дифференциальное уравнение с разделяющимися переменными. Для этого разделим переменные:

 Проинтегрируем уравнение:

Общее решение будет иметь вид:

Следовательно,  — температура хлеба в момент времени t.

Воспользуемся начальными условиями: t=0, y(0)=100.

 — частное решение.

Воспользуемся дополнительными условиями: t=20, y(20)= 60.

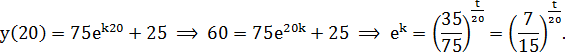
 — частное решение при данных дополнительных условиях.

Найдем момент времени, когда температура хлеба станет равной 30 °C.

.

Значит, Через 71 минуту от момента начала охлаждения температура хлеба понизится до 30 °C.

Таким образом, мы показали применение теории дифференциального моделирования к закону изменения температуры на примере задач практического содержания, что, не умиляя ценности рассмотрения изучаемого материала, способствует нашей заинтересованности в рассмотрении дифференциального моделирования других реальных процессов и применению теоретических знаний на практике.

Список литературы:

1.            Амелькин В.В. Дифференциальные уравнения в приложениях. / В.В. Амелькин. — М.: Наука, 1987. — 160 с.

2.            Виленкин Н.Я. и др. Дифференциальные уравнения. Учеб. пособие для студентов-заочников IV курса физ.-мат, / Н.Я. Виленкин, М.А. Доброхотова, А.Н. Сафонов. — М.: Просвещение, 1984. — 176 с.

3.            Демидович Б.П., Моденов В.П. Дифференциальные уравнения: Учеб. пособие. / Б.П. Демидович, В.П. Моденов. — СПБ.: Издательство «Лань», 2008. — 288 с.

4.            Матвеев Н.М. Дифференциальные уравнения. Учеб. пособие для студентов пед. ин-тов по физ.-мат. спец. — М.: Просвещение, 1988. — 256 с.

5.            Тихонов А.Н., Васильева А.Б., Свершников А.Г. Дифференциальные уравнения: Учеб. пособие для вузов. — 4-е изд. — М.: Физматлит, 2005. — 256 с.