ПРИМЕНЕНИЕ МЕТОДА ОСРЕДНЕНИЯ ДЛЯ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ПЕРЕДАЧИ ПОРОВОГО ДАВЛЕНИЯ
Секция: 10. Моделирование

VI Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
ПРИМЕНЕНИЕ МЕТОДА ОСРЕДНЕНИЯ ДЛЯ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ПЕРЕДАЧИ ПОРОВОГО ДАВЛЕНИЯ
Задачи подземной гидромеханики, связанные с движением флюидов в порах и трещинах горных пород, являются востребованными в связи с эксплуатацией нефтяных месторождений, длительными откачками жидкости с целью водоснабжения населения или осушения территорий перед строительством. Параметром, влияющим на напряженно-деформированное состояние флюидонасыщенных массивов пород, является так называемый коэффициент передачи порового давления на скелет породы, показывающий, какая часть давления жидкости является «активной» при формировании результирующих деформаций в породе. В работе развит теоретический способ определения этого коэффициента методом осреднения. Метод продемонстрирован с использованием конечно-элементной реализации. Проанализирована зависимость этого параметра от пористости грунта, формы пор, упругих свойств породы.
Коэффициент передачи порового давления на скелет породы, обозначаемый α, был введен в [5]. Коэффициент α является параметром, показывающим, какую часть порового давления необходимо учесть в полных напряжениях:
![]() (1)
(1)
где: ![]() — полные напряжения,
— полные напряжения,
![]() — эффективные (осредненные) напряжения в твердой фазе грунта, передающиеся по контактам между зернами породы,
— эффективные (осредненные) напряжения в твердой фазе грунта, передающиеся по контактам между зернами породы,
![]() — давление жидкости в порах. В [5] теоретически обосновано, что
— давление жидкости в порах. В [5] теоретически обосновано, что
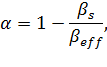
и предложен способ определения ![]() , основанный на использовании экспериментальных данных об относительном изменении объема образца породы при различных соотношениях полного гидростатического
, основанный на использовании экспериментальных данных об относительном изменении объема образца породы при различных соотношениях полного гидростатического 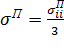 и порового
и порового ![]() давлений. Здесь
давлений. Здесь ![]() — сжимаемость материала скелета грунта,
— сжимаемость материала скелета грунта, ![]() — эффективная сжимаемость грунта.
— эффективная сжимаемость грунта.
Таким образом, учет коэффициента ![]() позволяет корректно определять эффективные напряжения. Последние важны, поскольку изменение объема породы, деформация грунта, его разрушение определяются величиной эффективных напряжений.
позволяет корректно определять эффективные напряжения. Последние важны, поскольку изменение объема породы, деформация грунта, его разрушение определяются величиной эффективных напряжений.
Безразмерный коэффициент ![]() может принимать значения от 0 до 1 в зависимости от величины напряжений и свойств грунта [6]. Например, для слабо сцементированных песчаников или несцементированных песков в условиях относительно небольших давлений
может принимать значения от 0 до 1 в зависимости от величины напряжений и свойств грунта [6]. Например, для слабо сцементированных песчаников или несцементированных песков в условиях относительно небольших давлений ![]() , так как коэффициент сжимаемости скелета таких пород
, так как коэффициент сжимаемости скелета таких пород ![]() значительно превышает коэффициент сжимаемости зерен
значительно превышает коэффициент сжимаемости зерен ![]() В этом случае можно считать, что полная величина пластового давления оказывает влияние на деформацию породы. Для низкопористых, сильно уплотненных пород с большим количеством закрытых пор
В этом случае можно считать, что полная величина пластового давления оказывает влияние на деформацию породы. Для низкопористых, сильно уплотненных пород с большим количеством закрытых пор ![]() , поскольку для таких пород коэффициент сжимаемости скелета становится соизмерим с коэффициентом сжимаемости материала твердой фазы. Следовательно, при больших напряжениях в скелете породы изменение пластового давления не приведет к возникновению деформаций в породе.
, поскольку для таких пород коэффициент сжимаемости скелета становится соизмерим с коэффициентом сжимаемости материала твердой фазы. Следовательно, при больших напряжениях в скелете породы изменение пластового давления не приведет к возникновению деформаций в породе.
Ввиду важности учета ![]() в моделях, описывающих деформирование флюидонасыщенного грунта под нагрузкой, коэффициент передачи порового давления в том или ином виде используют многие исследователи [1; 5; 6]. В то же время коэффициент
в моделях, описывающих деформирование флюидонасыщенного грунта под нагрузкой, коэффициент передачи порового давления в том или ином виде используют многие исследователи [1; 5; 6]. В то же время коэффициент ![]() является сложно определяемым параметром. Не случайно разные авторы предлагают свои способы его определения, как теоретические, так и экспериментальные.
является сложно определяемым параметром. Не случайно разные авторы предлагают свои способы его определения, как теоретические, так и экспериментальные.
Например, в уравнение равновесия модели М. Био [1] входят коэффициенты ![]() и
и ![]() , определяющие соответственно изменение полного объема грунта (как эффективного материала) и объема пор (равного объему воды при полном насыщении породы) при изменении давления жидкости. Чтобы проинтерпретировать константы
, определяющие соответственно изменение полного объема грунта (как эффективного материала) и объема пор (равного объему воды при полном насыщении породы) при изменении давления жидкости. Чтобы проинтерпретировать константы ![]() и
и ![]() , Био предлагает рассмотреть образец породы, заключенный в тонкую резиновую оболочку. Напряжения, приложенные к грунту, равны 0. Если через тонкую трубку, проходящую через стенку оболочки, сдренировать воду из грунта, приложив отрицательное давление (-p) к трубке, то относительное изменение объема воды θ и относительное изменение полного объема грунта
, Био предлагает рассмотреть образец породы, заключенный в тонкую резиновую оболочку. Напряжения, приложенные к грунту, равны 0. Если через тонкую трубку, проходящую через стенку оболочки, сдренировать воду из грунта, приложив отрицательное давление (-p) к трубке, то относительное изменение объема воды θ и относительное изменение полного объема грунта ![]() будут равны:
будут равны:
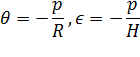
Интересно заметить, что коэффициент ![]() , предложенный Феттом [5], связан с коэффициентами
, предложенный Феттом [5], связан с коэффициентами ![]() и
и ![]() , введенными Био, с помощью следующего соотношения:
, введенными Био, с помощью следующего соотношения:
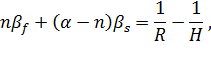
где: ![]() — эффективная пористость грунта,
— эффективная пористость грунта,
![]() — сжимаемость жидкости.
— сжимаемость жидкости.
Также важно подчеркнуть, что система дифференциальных уравнений, описывающая деформирование водонасыщенного грунта, решается наиболее просто при ![]() [2; 3]. Поэтому полезно оценить, насколько значения
[2; 3]. Поэтому полезно оценить, насколько значения ![]() близки к единице в зависимости от параметров водонасыщенного грунта.
близки к единице в зависимости от параметров водонасыщенного грунта.
В настоящей работе предложен способ определения коэффициента передачи порового давления на основе метода осреднения [4]. Для краткости рассмотрим задачу деформирования пористой среды в результате действия только давления жидкости. В силу линейности силовое воздействие на скелет может быть найдено отдельно. Предполагается, что читатель знаком с терминологией метода осреднения. Предполагаем среду двухфазной, состоящей из каркаса и пор, полностью насыщенных жидкостью. Перемещения в скелете грунта представим следующим асимптотическим разложением:
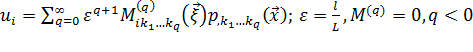 (2)
(2)
здесь ![]() — осредненное давление жидкости в пористой среде,
— осредненное давление жидкости в пористой среде, ![]() — «быстрые» координаты, определенные в представительной области, а
— «быстрые» координаты, определенные в представительной области, а ![]() — «медленные» координаты, определенные для области всего грунта. Локальные функции
— «медленные» координаты, определенные для области всего грунта. Локальные функции ![]() быстрых координат -го уровня определены в представительной области, размеры которой в
быстрых координат -го уровня определены в представительной области, размеры которой в ![]() раз меньше всей области, занимаемой грунтом. Проводя формальные выкладки, в первом приближении будем иметь:
раз меньше всей области, занимаемой грунтом. Проводя формальные выкладки, в первом приближении будем иметь:
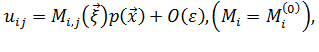 (3)
(3)
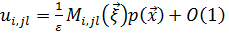 (4)
(4)
Подставив выражения (3) и (4) в уравнение равновесия, получим локальные задачи для функций ![]() и выражение для среднего напряжения:
и выражение для среднего напряжения:
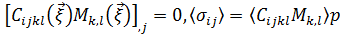 (5)
(5)
Таким образом, напряжения в уравнении (5) — это напряжения, возникающие в результате действия порового давления. Сопоставив уравнение (1) c уравнением (5), приходим к выводу, что асимптотический анализ приводит, вообще говоря, к тензору передачи давления ![]() :
:
![]()
С помощью теоретического анализа или вычислений можно выяснить, в каких случаях данный тензор является шаровым (или близок к шаровому), т. е. ![]() . Ниже рассмотрим иллюстрирующие примеры. Для простоты предположим, что среда имеет периодическую структуру и находится в плоском деформированном состоянии.
. Ниже рассмотрим иллюстрирующие примеры. Для простоты предположим, что среда имеет периодическую структуру и находится в плоском деформированном состоянии.
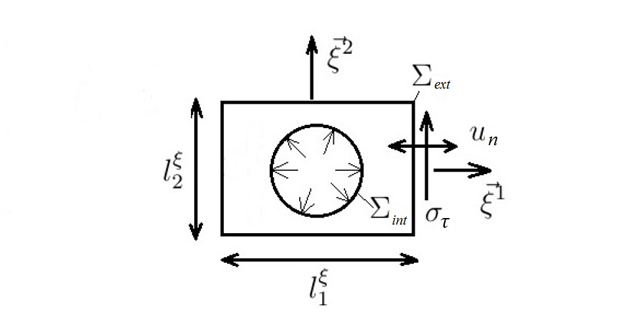
Рисунок 1. Модель ячейки с одной круглой порой для решения локальной задачи
Для двояко симметричной поры, изображенной на Рис. 1, постановка локальной задачи имеет вид:
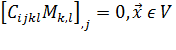 (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]()
Опишем вычисление коэффициентов ![]() , которые при единичном поровом давлении (p=1) численно равны средним напряжениям
, которые при единичном поровом давлении (p=1) численно равны средним напряжениям ![]() , возникающим в локальной задаче (6), (7), (8):
, возникающим в локальной задаче (6), (7), (8):
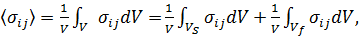 (9)
(9)
где: ![]() есть область ячейки периодичности,
есть область ячейки периодичности,
![]() — объемы, занимаемые твердой и жидкой фазой соответственно.
— объемы, занимаемые твердой и жидкой фазой соответственно.
Сначала вычислим интеграл 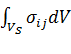 , преобразуя его к интегралу по границе. Действительно, используя формулу
, преобразуя его к интегралу по границе. Действительно, используя формулу ![]() (верную, поскольку
(верную, поскольку ![]() ,
, ![]() ), получим:
), получим:
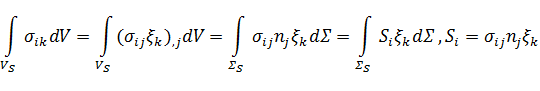
Учтем, что ![]() (см. рис. 1). Очевидно, что интеграл по внутренней границе для твердой фазы будет равен такому же интегралу по жидкой фазе, взятому с противоположным знаком. Следовательно, остается вычислить интеграл по внешней границе для твердой фазы.
(см. рис. 1). Очевидно, что интеграл по внутренней границе для твердой фазы будет равен такому же интегралу по жидкой фазе, взятому с противоположным знаком. Следовательно, остается вычислить интеграл по внешней границе для твердой фазы.
Обозначим ![]() , где
, где ![]() — вертикальные, а
— вертикальные, а ![]() — горизонтальные границы ячейки. Тогда, учитывая, что на
— горизонтальные границы ячейки. Тогда, учитывая, что на ![]() :
: ![]() = (0,1),
= (0,1), ![]() = 0, и, следовательно,
= 0, и, следовательно, ![]() = 0, получим:
= 0, получим:
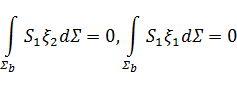
Так как на ![]()
![]() — четная,
— четная, ![]() — нечетная, имеем
— нечетная, имеем
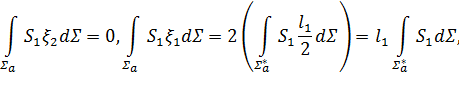
где: ![]() — правая сторона ячейки. Для
— правая сторона ячейки. Для ![]() вычисление проводится аналогично.
вычисление проводится аналогично.
Тензор напряжений является шаровым, если у нас симметричная квадратная ячейка. В этом случае для вычисления коэффициента α достаточно вычислить только ![]() . Сопоставив уравнения (5) и (9) и учитывая все дальнейшие выводы, имеем:
. Сопоставив уравнения (5) и (9) и учитывая все дальнейшие выводы, имеем:
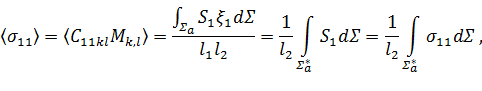
Значение интеграла 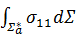 мы получаем из расчета с помощью МКЭ. Коэффициент α рассчитывается следующим образом:
мы получаем из расчета с помощью МКЭ. Коэффициент α рассчитывается следующим образом:
![]()
Для вычисления коэффициента α была выбрана квадратная ячейка со стороной, равной 1.
На рис. 2 показана зависимость коэффициента передачи порового давления α от формы поры. У всех моделей одинаковая пористость: n = 28,3 % и одинаковые упругие свойства материала каркаса (коэффициент Пуассона): ν = 0,3. Как видно, наибольшее значение α наблюдается у крестообразной поры и у поры в форме звезды. Чем ближе форма поры к круглой, тем меньше α.
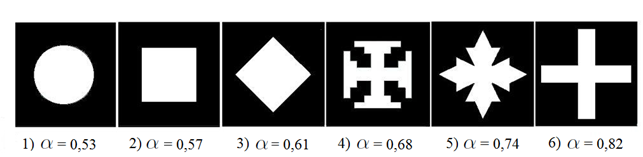
Рисунок 2. Зависимость коэффициента α от формы поры
(n = 28,3 %, ν = 0,3)
Зависимость α от пористости изучалась на примере одной круглой поры. Получена четкая закономерность (рис. 3а): коэффициент передачи порового давления монотонно возрастает с увеличением пористости. Для проверки были проведены расчеты α для модели с четырьмя круглыми порами радиусом 0.1 (пористость модели 12,6 %) и для модели с 25-ю круглыми порами радиусом 0.05 (пористость 19,6 %). Значения коэффициента α совпали с результатами расчетов для моделей с одной круглой порой (α = 0,29 и 0,41 соответственно).
Проанализирована зависимость коэффициента передачи порового давления от коэффициента Пуассона ν для ячеек с одной круглой порой, но разной пористости (рис. 3б) и для сред с одинаковой пористостью (n = 28,3 %), но различной формой поры (рис.3в). Видно, что во всех случаях зависимость почти линейная, причем угол наклона графика не зависит от пористости, но зависит от формы поры: наибольший угол — у модели с круглой порой, наименьший — с крестообразной порой.
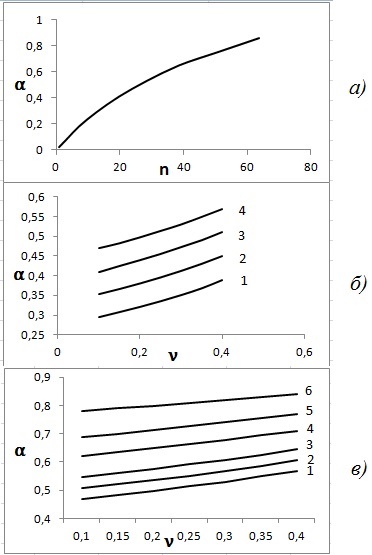
Рисунок 3. Зависимость коэффициента α от пористости n (а) (ν = 0.3) и от коэффициента Пуассона ν (б, в). Значения пористости расчетных моделей на рис. 3б: ![]() = 15,9 %,
= 15,9 %, ![]() = 19,36 %,
= 19,36 %, ![]() = 23,76 %,
= 23,76 %, ![]() = 28,27 %. В качестве моделей для расчета графиков, показанных на рис. 3в брались образцы, показанные на рис. 2
= 28,27 %. В качестве моделей для расчета графиков, показанных на рис. 3в брались образцы, показанные на рис. 2
Таким образом, в работе описан теоретический способ определения коэффициента передачи порового давления α на основе метода осреднения. Для демонстрации метода были проведены расчеты с помощью конечно-элементного программного комплекса. Была проанализирована зависимость этого параметра от формы пор, пористости, упругих свойств грунта. Результаты расчетов показали, что значения коэффициента α сильно варьируют в зависимости от структуры и свойств грунта. Например, наличие угловатых, вытянутых пор увеличивает значение α в 1,5 раза, а в зависимости от пористости грунта значение α меняется от 0 до 1. Следовательно, результаты исследований подтверждают необходимость учета истинного значения коэффициента α при изучении напряженно-деформированного состояния конкретных объектов.
Список литературы:
1. Добрынин В.М. Физические свойства нефтегазовых коллекторов в глубоких скважинах. — М.: Недра, 1965. — 163 с.
2. Киселев Ф.Б., Шешенин С.В. Разностная схема для задачи нестационарной фильтрации в слоистых грунтах.// Известия Российской академии наук. Механика твердого тела. 1996. № 3. — С. 129.
3. Победря Б.Е. Механика композиционных материалов. — М.: Изд-во Моск. ун-та, 1984. — 336 с.
4. Шешенин С.В., Какушев Э.Р., Артамонова Н.Б. Моделирование нестационарной фильтрации, вызванной разработкой месторождений.// Вестник Московского университета. Серия 1. Математика. Механика. 2011. № 5. — С. 66—68.
5. Biot M.A. General theory of three-dimensional consolidation.// Journal of Applied Physics. 1941. Vol.12. — P. 155—164.
6. Fatt I. Compressibility of sandstones at low to moderate pressures.// Bulletin of the American Association of Petroleum Geologist. 1958. Vol. 42. № 8. — P. 1924—1957.





