О ДИФФЕРЕНЦИАЛЬНОМ МОДЕЛИРОВАНИИ ЗАКОНА ДВИЖЕНИЯ МАТЕМАТИЧЕСКОГО МАЯТНИКА

Первенствующее значение в процессе построения обыкновенных дифференциальных моделей имеет знание законов той области науки, с которой связана природа изучаемой задачи. Так, например, в механике это могут быть законы Ньютона, в теории электрических цепей — законы Кирхгофа, в теории скоростей химических реакций — закон действия масс и т. д. Конечно, на практике приходится иметь дело и с такими случаями, когда неизвестны законы, позволяющие составить дифференциальное уравнение, и поэтому необходимо прибегать к различным предположениям, касающимся протекания процесса при малых изменениях параметров — переменных. К дифференциальному уравнению тогда приводит предельный переход. В случае, если окажется, что результаты исследования полученного дифференциального уравнения как математической модели согласуются с данными, полученными опытным путем, то это и будет означать, что высказанная гипотеза правильно отражает истинное положение вещей.

Мы на примере закона движения математического маятника покажем возможность использования обыкновенных дифференциальных уравнений в процессе познания окружающей нас действительности.

Найдем закон движения и определить период Т математического маятника длины l при малых отклонениях. При условии, что t=0, S=a, =0, где S(t) — величина дуги, на которую отклонился маятник в момент t.

На маятник действует сила упругости нити F и сила тяжести Р. Когда он находиться в равновесии, то Р + F=0. Результирующая сила F₁, направленная по касательной к траектории в сторону положения равновесия возникает, когда маятник отклонен.

Из рисунка 1 видно, что │ F₁│= p sinα. Кроме того, по второму закону Ньютона, который гласит, что производная по времени от количества движения материальной точки равна действующей на неё силе .

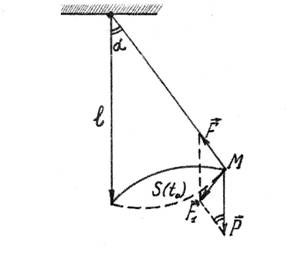
Рисунок 1. Модель математического маятника

Дифференциальное уравнение получается в проекции на горизонтальную ось. Минус в правой части получается за счет того, что частная производная второго порядка от величины дуги по времени  отрицательна).

Произведя несложные преобразования, получим

,

g.

Кроме того, при малых α, sinα ≈ α ≈ S/ l.

Поэтому уравнение примет вид — линейное однородное дифференциальное уравнение с постоянными коэффициентами. Решим его. Оно имеет вид:

Составим характеристическое уравнение

λ² — k = 0 → λ = ±і(k<0)

Фундаментальная система решений имеет вид:

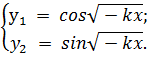
Общее решение искомого дифференциального уравнения имеет вид:

у= С₁sin = С₂ cos.

Воспользовавшись начальными условиями, t=0, S= 0,, получим

S = α cos .

Это частное решение.

Найдем период колебания маятника, используя периодичность функции косинус. Получим:

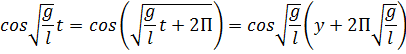
Отсюда следует, что

.

Рассматривая вопрос о неточности маятниковых часов, мы придём к составлению дифференциальной модели. Пусть дана идеализированную модель маятниковых часов, состоящая из стержня длиной l и гири массой m на его конце (масса стержня предполагается такой, что её можно не принимать в расчет по сравнению с массой гири).

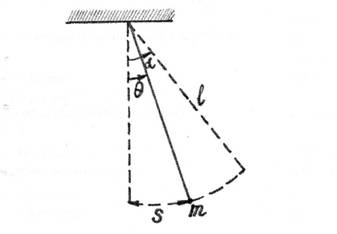
Рисунок 2. Идеализированная модель маятниковых часов

Если гирю отклонить на угол и затем отпустить, то в соответствии с законом сохранения энергии

,                                 (*)

где: v— скорость движения гири,

g — ускорение силы тяжести.

Длина дуги, по которой гиря отклоняется от положения равновесия на угол θ, определяется равенством S= lθ, в случае если рассматривать только малые отклонения гири от положения равновесия. Тогда  и соотношения (*) приводит к дифференциальному уравнению:

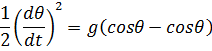
Полученное дифференциальное уравнение можно записать в виде:

 .

Положим, что Т — период колебания маятника, тогда

.

Отсюда получим .

Последняя формула показывает зависимость периода колебания маятника от угла α. Данная зависимость и является основной причиной неточности маятниковых часов, ведь практически каждый раз гиря отклоняется в крайнее положение на угол, отличный от α.

Так как

то

                           (**)

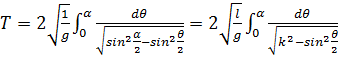где .

Делая замену  заметим, что когда θ возрастает от 0 до α, то φ возрастает от 0 до π/2, причем

или

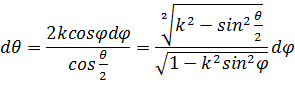
Если воспользоваться последним выражением, то формулу (**) можно записать в виде:

которая содержит так называемый эллиптический интеграл первого рода

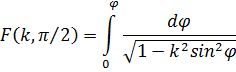
Эллиптические интегралы не могут быть вычислены в элементарных функциях. Дифференцируя уравнение  по переменной t, получим:

.

Таким образом, в исследуемом вопросе о законе движения математического маятника пришли к дифференциальной модели реального процесса. Это обстоятельство дает нам возможность рассмотрения дифференциального моделирования и в других областях знаний, а также его практическое применение.

Список литературы:

1.            Амелькин В.В. Дифференциальные уравнения в приложениях. / В.В. Амелькин. — М.: Наука, 1987.—160 с.

2.            Виленкин Н.Я. и др. Дифференциальные уравнения. Учеб. Пособие для студентов-заочников в IV курса физ-мат, фак. / Н.Я. Виденкин, М.А. Доброхотова, А.Н. Сафонов. — М.: Просвещение, 1984. — 176 с.

3.            Демидович Б.П., Моденов В.П. Дифференциальные уравнения: Учебное пособие. / Б.П. Демидович, В.П. Моденов. — СПб.: Издательство «Лань», 2008. — 288 с.

4.            Матвеев Н.М. Дифференциальные уравнения: Учеб. пособие для студентов пед. ин-тов по физ.-мат. спец. / Н.М. Матвеев М.: Просвещение, 1988. — 256 с. 

5.            Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения: Учеб.: Для вызов. — 4-е изд. — М.: ФИЗМФТЛИТ, 2005. — 256 с.

6.            Шипачев В.С. Высшая математика : Учебник для вузов / В.С. Шипачев. — 6-е изд., стер. — М. : Высшая школа, 2003. — 479 с.