ЗАВИМОСТЬ ТЕМПЕРАТУРЫ ТЕПЛОНОСИТЕЛЯ ОТ ДЛИНЫ ТРУБОПРОВОДОВ СИСТЕМЫ ОТОПЛЕНИЯ

В статье рассматривается вариант применения дифференциальных уравнений в частных производных второго порядка для решения ряда задач энергосберегающих технологий

Теоретические исследования динамических свойств системы централизованного теплоснабжения с зависимым подключением тепловой нагрузки носят решающий характер для создания соответствующих механизмов управления [2; 3]. Предварительно отметим, что будем вести рассуждение для типоразмера стальных тонкостенных электросварных труб с отношением внутреннего и внешнего диаметров , ГОСТ 10704-91.

Предназначаемая математическая модель основана на законах тепломассопереноса. Предполагается, что на исследуемом участке внутри горизонтальной цилиндрической трубы присутствует сплошная непрерывная среда (нагретая вода), характеристики процессов переноса которой являются непрерывными функциями координат и времени. При решении нестационарных задач вынужденного конвективного теплообмена используется дифференциальное уравнение переноса теплоты в движущейся среде с известной скоростью:

,                      (1)

где: 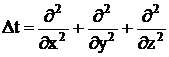 — оператор Лапласа в прямоугольной системе координат;

t — температура теплоносителя, ^оС;

l — коэффициент теплопроводности, Вт/ м×^оС;

с и r — соответственно теплоемкость и плотность теплоносителя, Дж/кг×^оС и кг/м²;

x,y,z — координаты в прямоугольной системе координат, м;

 — проекции вектора скорости теплоносителя, м/с;

 — соответственно интенсивности внутренних источников и тепловых потерь охлажденного теплоносителя, Дж/ с×м³;

t — время, с.

Рисунок 1. Перенос теплоты в движущейся среде

с постоянной скоростью W_x

Рассмотрим стационарный режим работы системы трубопроводов (расход и температура рабочего тела в нормальном сечении неизменные, движение потока жидкости направлено вдоль оси ОХ, , рис. 1). В этом случае в дифференциальном уравнении (1) справедливы соотношения  . Учитывая, что величина Q_V в теплоносителе практически отсутствует, уравнение (1) резко упрощается:

.                                              (2)

Преобразуем (2) к виду:

                                           (3)

где: граничные условия задаются значениями:  при  и  — соответственно температуры теплоносителя на входе в подающий и на выходе из обратного трубопроводов, ^оС.

Согласно [1] величина Q определяется по формуле:

                                                 (4)

где:  — соответственно температура теплоносителя (горячей воды) и температура воздуха в отапливаемом помещении (тепловой нагрузке), ^оС;

 — длина контура трубопровода тепловой нагрузки, м; ;

 — коэффициент теплопередачи контура трубопровода к тепловой нагрузке,  Вт/ м²×^оС;

— эффективный диаметр трубопровода, м;

Следует отметить, что  определяется по формуле:

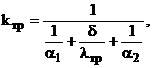                                                        (5)

где:  — соответственно коэффициенты теплоотдачи от теплоносителя к трубопроводу и от трубопровода к тепловой нагрузке, Вт/ м²×^оС;

 — толщина стенок трубопровода, м;

λ_{тр —} коэффициент теплопроводности материала трубопровода, Вт/ м×^оС.

Величина  выбирается в зависимости от соотношения между величинами  и  при условии, что , ( Вт/м²×^оС;  Вт/ м²×^оС) по формуле:

                                                        (6)

Коэффициенты теплоотдачи λ₁ и λ₂ определяются соответственно по формуле:

,                                                                  (7)

где:   — соответственно коэффициенты тепловодности горячей воды и воздуха в обогреваемом помещении, Вт/ м×^оС;

 — критерий Нуссельта для турбулентно текущей горячей воды в трубопроводе круглого сечения, причем:

,                     (8)

где:  — критерий Рейнольдса для горячей воды в трубопроводе ();

— соответственно значения критерия Прандтля для горячей воды и внутренней стенки трубы;

— коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по трубе. Если отношение , то , где  — длина трубы, м, d — внутренний диаметр трубы, м.

Учитывая (4), и переходя от частных производных к обыкновенным, получим:

.                                   (9)

Представим (9) в более удобный для интегрирования форме:

.                          (10)

Полагая, что  (установившаяся температура в тепловой нагрузке), получим дифференциальное уравнение второго порядка с постоянными коэффициентами и правой частью в виде константы (полинома нулевой степени). В этом случае будем рассматривать температуру t как функцию одной переменной x т. е. .

Решим предварительно однородное дифференциальное уравнение:

.                                (11)

Для этого составим соответствующее характеристическое уравнение:

                                 (12)

корни которого имеют вид:

                              (13)

где дискриминант D характеристического уравнения (12) определяется по формуле:

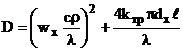.                                       (14)

Очевидно, что a₁<0, a₂>0. Оценим величину D. Из данных эксперимента следует:  м/с;  Дж/ кг×^оС; кг/м³;  Вт/м×к;  Вт/м²×к;  м; м. В этом случае D изменяется в пределах: м^-2. Зная размах D, соответственно вычислим значения а₁ и а₂:  . Учитывая, что  и , получим общее решение  однородного уравнения (11):

,                                          (15)

где: — const;

 — основание натурального логарифма.

Определим частное решение  неоднородного дифференциального уравнения (10) по известной правой части:

,

в которой число b=0 не является корнем характеристического уравнения (12). Тогда ,будем искать в виде: 

,                                        (16)

где: — полином нулевой степени.

В этом случае имеем:

                                                     (17)

Определяем А, дважды продифференцировав  и подставив в уравнение (10). Получим:

.                                                        (18)

Найдем общее решение неоднородного дифференциального уравнения (10)  в виде . Учитывая (15) и (18), имеем:

.                                             (19)

Найдем частное решение  , определив С₁ и С₂. Учитывая граничные условия, получим:

    ,          (20)

где: — соответственно температура теплоносителя в падающем и обратном трубопроводе сети.

Найдем постоянные интегрирования С₁ и С₂ решив систему:

                                        (21)

тогда:

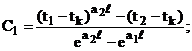
                       (22)

Очевидно, что . Так как , то , тогда , т. е. ; аналогично , то  и .

Исследуем зависимость (19) и построим график . Вычислим первую производную  

                     (23)

Учитывая, что , получим:

                           (24)

Вычислим вторую производную

             (25)

Учитывая, что на отрезке , получим:

                         (26)

Ввиду этого делаем вывод, что график функции  выпукл вверх на этом отрезке, рис. 2.

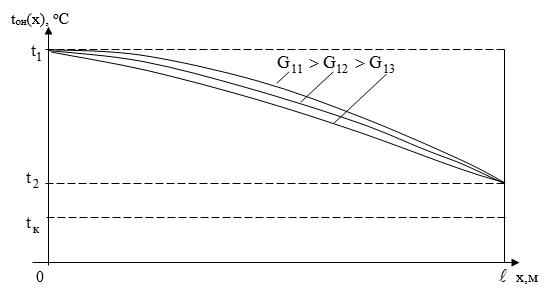
Рисунок 2. Зависимость температуры носителя  от длины х горизонтальной трубы круглого сечения

Из [3] следует, что с ростом расхода теплоносителя , поступающего в тепловую нагрузку из подающего трубопровода, увеличивается тепловой поток, проходящий через стенки трубы в отапливаемые помещения.

Отметим, что других решений дифференциального уравнения не существует, т. к. случай  не имеет места.

Анализируя решение характеристического уравнения (12) отметим, что , поэтому формула (19) не дает ни устойчивого, ни асимптотически устойчивого решения [3], что требует автоматического регулирования.

Выводы:

1.  Получена зависимость изменения температуры от длины главного циркуляционного кольца.

2.  Доказано, что полученная зависимость не дает ни устойчивого, ни асимптотически устойчивого решения, что требует автоматического регулирования.

Список литературы:

1.            Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача. — М.: Энергия, 1981. — 417 с.

2.            Федоров С.С., Кобелев Н.С., Тютюнов Д.Н. Алгоритм автоматического управления приводом системы отопления зданий и сооружений // ЮЗГУ.2011.№ 5.4.2. 335-339.

3.            Федоров С.С., Кобелев Н.С., Тютюнов Д.Н. Регулирование параметров микроклимата зданий и сооружений в зависимости от теплопроводности строительных материалов // Вестник МГСУ. 2011. № 3. — с. 415—421.