АНАЛИЗ АЛГОРИТМА ОБРАТНОГО РАСПРОСТРАНЕНИЯ ОШИБКИ НЕЙРОННОЙ СЕТИ

В статье изложены основы нейронной сети, а также проведен анализ функционирования алгоритма обратного распространения ошибки.

На сегодняшний день, нейронная сеть является одним из способов интеллектуального анализа данных. Интеллектуальный анализ данных позволяет решить такие проблемы, как: классификация и кластеризация, прогнозирования, распознавание образов, сжатия данных и ассоциативная память, диагностика заболеваний и т. д.

Нейронные сети — это одно из направлений исследований в области искусственного интеллекта, основанное на попытках воспроизвести нервную систему человека. А именно, способность нейронной сети обучаться и исправлять ошибки, что должно позволить смоделировать, хотя и достаточно грубо, работу человеческого мозга [1].

Нейронная сеть — это математическая модель человеческого мозга, состоящая из многих простых вычислительных элементов (нейронов) рисунок 1, работающих параллельно, функция которых определяется структурой сети, а вычисления производятся в самих элементах. Считается, что способность мозга к обработке информации в основном обусловлена функционированием сетей, состоящих из таких нейронов [1; 2].

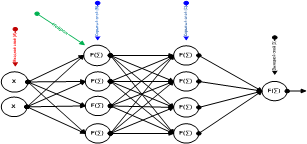
Рисунок 1. Многослойная нейронная сеть

Рассмотрим нейронную сеть стандартной архитектуры (рисунок 1), которая обычно имеет несколько слоев: А — рецепторный слой, на который подаются входные данные; B,C — скрытые слои, нейроны которых интерпретируют полученную информацию; D — выходной слой, предоставляющий реакцию нейронной сети.

Каждый слой сети состоит из нейронов. Нейрон — это основной элемент вычисления, нейронной сети. На рисунке 2 показана его структура.

В состав нейрона входит умножители, сумматоры и нелинейный преобразователь. Синапсы осуществляют связь между нейронами и умножают входной сигнал на число, характеризующее силу связи – веса синапсов.

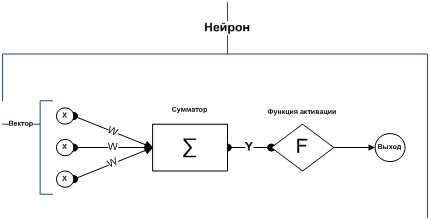
Рисунок. 2. Структура искусственного нейрона

Сумматор выполняет сложение сигналов, поступающих по синоптическим связям от других нейронов или внешних входных сигналов. Нелинейный преобразователь реализует нелинейную функцию одного аргумента — выход сумматора. Это функция называется «функцией активации» или «передаточной функцией» нейрона. Нейрон в целом реализует скалярную функцию векторного аргумента.

Математическая модель нейрона описывает соотношениями

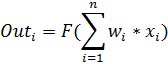
где — вес синапса ; s— результат суммирования; x_i — компонент входного вектора ; y — выходной сигнал нейрона; n — число входов нейрона; — функция активации;

Главная задача в процессе разработки нейронной сети, является этап обучения, т. е. корректировки весов сети, для минимизации ошибки на выходе нейронной сети.

Стандартная нейронная сеть прямого распространения приведена на рисунке 3, также известна как многослойный персептрон(MLP). Обратите внимание, что узлы входного уровня отличаются от узлов в других слоях, это означает, что никакая обработка не происходит в этих узлах, они служат только в качестве входов сети.

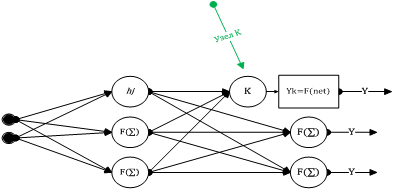
Рисунок 3. Стандартная сеть с прямым распространением

Каждый узел вычисляет взвешенную сумму его входов, и использует его как входные данные функции преобразованияВ классическом многослойном персептроне, функция преобразования — сигмоид.

Сигмоида — это гладкая монотонная нелинейная S — образная функция, которая часто применяется для «сглаживания» значений некоторой величины.

                          (1)

Рассмотрим узел  в скрытом слое. Его выход  представляет  где , функция активации (сигмоида), являются взвешенной суммой выходов узлов входного слоя A

         (2)

аналогично, выход каждого узла в каждом слое.

Для удобства, мы можем рассмотреть входы сети, как входной вектор , где . Аналогично, выход для сети можно рассматривать как вектор выхода , где . Учебный набор для сети можно представить рядом пар  входных векторов и желаемых векторов выхода :.

Каждый раз, когда входной вектор от учебного набора  применен к сети, сеть производит фактический выход . Мы можем таким образом определить квадратичную ошибку для этого входного вектора, суммируя квадратичные ошибки в каждом узле выхода [3; 4]:

.                      (3)

Главная задача, как уже было сказано в обучение нейронной сети, это минимизировать квадратичную ошибку. Мы можем также определить полную квадратичную ошибку , суммирую все пары входа — выхода в учебном наборе:

                                         (4)

Для минимизации квадратичной ошибки, будем использовать алгоритм градиентного спуска. Определим какое направление является «скоростным спуском» на поверхности ошибок и изменим каждый вес  так, чтобы мы двигались в этом направление. Математически это означает, что каждый вес  будет изменен на небольшое значение  в направлении уменьшения :

         (5)

Здесь  — вес во время  и  — обновленный вес. Уравнение 5 называется обобщенным дельта — правилом. Чтобы выполнить градиентный спуск, нужно найти частную производную  каждого веса.

Для корректировки весов, между скрытым и выходным слоем, нужно найти частную производную, для каждого узла выходного слоя.

                              (6)

Таким образом, была найдена частная производная ошибки  по весам  и можем использовать этот результат в уравнение 5, чтобы выполнить градиентный спуск для всех весов между скрытым и выходным слоями.

Теперь рассмотрим веса, между входным слоем и скрытым слоем.

                (7)

Была получена частная производная ошибки  по весу на основе известных величин (многие из которых мы уже вычислили при получении ).

Рассмотрим алгоритм обратного распространения ошибки в виде блок-схемы (рисунок 4).

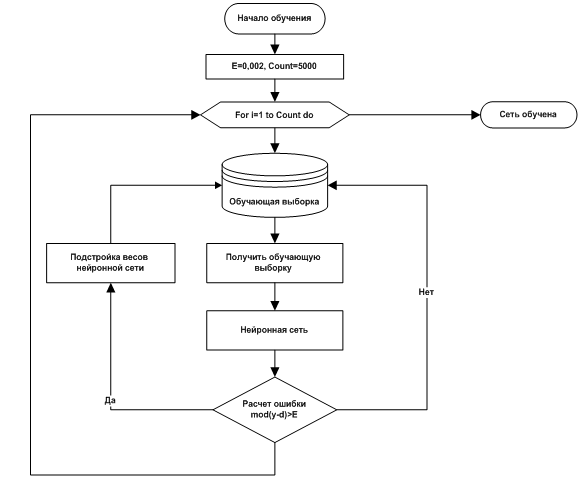
Рисунок 4. Алгоритм обучения нейронной сети прямого распространения

Принцип функционирования алгоритма обратного распространения ошибки, заключается в использование метода градиентного спуска и корректировки весов, для минимизации ошибки нейронной сети.

В процессе разработки нейронной сети, одним из основных этапов является обучения нейронной сети. В данной статье был проведен анализ алгоритма обратного распространения ошибки, которая использует метод градиентного спуска, для корректировки весов.

Список литературы:
1.    Рассел С., Норвиг П. Искусственный интеллект. Современный подход. — М.: Изд-во «Вильямс», 2006. — 1408 с.
2.    Хайкин С. Нейронные сети: полный курс. — М.: Изд-во «Вильямс», 2006. — 1104 с.
3.    Алгоритм обратного распространения ошибки. — [Электронный ресурс] — Режим доступа. — URL:http://www.aiportal.ru/articles/neural-networks/back-propagation.
4.    Алгоритм обратного распространения ошибки. — [Электронный ресурс] — Режим доступа. — URL:http://masters.donntu.edu.ua/2006/kita/kornev/library/l10.htm.