РЕАЛИЗАЦИЯ МЕТОДА РОЯ ЧАСТИЦ НА NVIDIA CUDA

Стаи птиц и косяки рыб демонстрируют увлекательное скоординированное коллективное поведение. Птицы, перемещаясь в произвольном порядке, ищут себе пропитание и одновременно следят за кем-либо другим и тем, кто ближе к еде. Способность собираться в стаи имеет ряд преимуществ для индивидуумов: увеличивается эффективность поиска пищи, усовершенствуется избегание хищников, повышаются возможности спаривания. Вместе с каждым индивидуумом, использующим только локальную информацию, вся стая демонстрирует изменчивое когерентное (связное) движение, которое выглядит идеально синхронизированным.

Такое подобное стае движение может быть смоделировано на базе трех основных принципов поведения, в которых используется только информация от соседей:

1)  избегать столкновений с ближайшими особями из стаи,

2)  подбирать скорость в соответствии со скоростями особей, движущимися рядом

3)  стараться оставаться на малом расстоянии от ближайших особей.

Целью данной работы является реализация метода роя частиц для решения задачи многомерной глобальной безусловной оптимизации на графических процессорах

Метод роя частиц был первоначально разработан для графического моделирования хореографии стаи птиц, в дальнейшем он был развит для различных прикладных задач.

Он относится к классу поведенческих эволюционных методов глобальной оптимизации. Поведенческие методы основаны на моделировании коллективного поведения самоорганизующихся живых или неживых систем, состоящих из простых агентов. Ключевыми идеями поведенческих методов являются децентрализованность, взаимодействие агентов, простота поведения агентов.

Данный метод, как и все алгоритмы, принадлежащие к семейству эволюционных алгоритмов, является стохастическим, не требующим вычисления градиента, что позволяет использовать его в случаях, где вычисление градиента невозможно, либо имеет высокую вычислительную сложность.

Существует несколько разновидностей метода. Например, в каноническом методе роя частиц, предложенном в 1995 году в работе Kennedy, Eberhart [3, с. 1942—1948], на каждой итерации при определении следующего положения частицы учитывается информация о наилучшей частице из числа «соседей» данной частицы, а также информация о данной частице на той итерации, когда этой частице соответствовало наилучшее значение целевой функции.

В методе роя частиц оптимизации агентами являются частицы в пространстве параметров задачи оптимизации. Каждая частица имеет определенное местоположение и скорость в пространстве поиска и, таким образом, характеризует определенное решение. Подобно птицам, перемещающимся в окружающей среде в поисках пищи или при уклонении от хищников, частицы пролетают через пространство поиска, изыскивая высококачественные решения по следующему алгоритму:

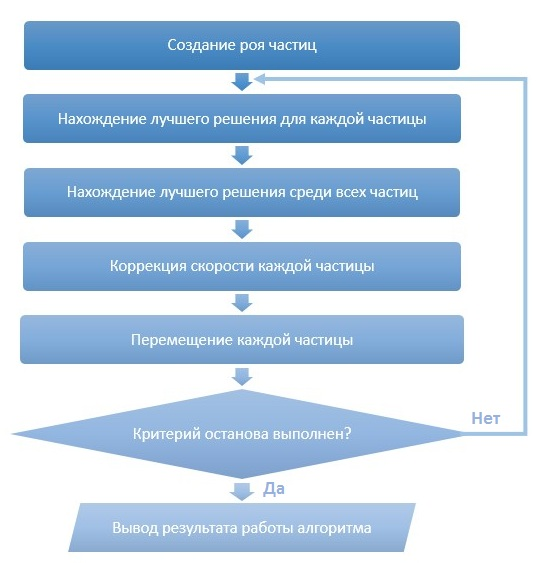
В каждый момент времени частицы имеют в этом пространстве некоторое положение и вектор скорости, который меняется на каждой итерации по следующей формуле:

где коэффициент , названный Юхи Ши (Yuhui Shi) и Расселом Эберхартом коэффициентом инерции [4, с. 69—73], определяет баланс между широтой исследования и вниманием к найденным субоптимальным решениям. В случае, когда , скорости частиц увеличиваются, они разлетаются в стороны и исследуют пространство более тщательно. В противном случае, скорости частиц со временем уменьшаются, и скорость сходимости в таком случае зависит от выбора параметров — постоянных ускорения, — лучшая найденная частицей точка, — лучшая точка из пройденных всеми частицами системы, — текущее положение частицы, а функция возвращает случайное число от 0 до 1 включительно.

После вычисления направления вектора , частица перемещается в точку. Основываясь на наилучшем достигнутом данной частиц экстремуме и информации о наиболее оптимальных частицах в рое, в случае необходимости, обновляются значения лучших точек для каждой частицы и для всех частиц в целом [1]. После этого цикл повторяется.

В работе было выбрано следующее условие завершения алгоритма: работа завершается по достижению некоторого определенного числа итераций, в течение которых решение не было улучшено.

На основе разработанного алгоритма реализована программа, апробированная на сферической функции и функции Растригина.

На рисунках 1 и 2 приведены результаты работы метода роя частиц в зависимости от количества частиц в рое (8, 16, 32, 64 и 128 частиц) для двумерного пространства.

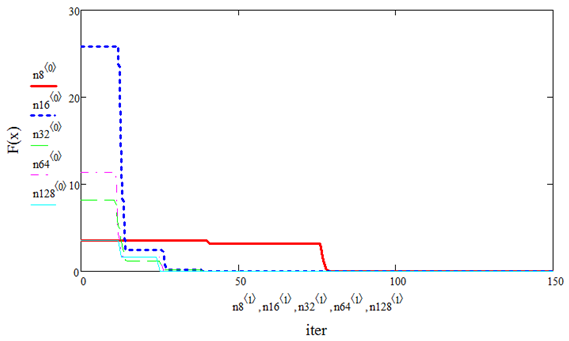
Рисунок 1. Скорость сходимости метода в зависимости от количества частиц в рое для сферической функции (n=2)

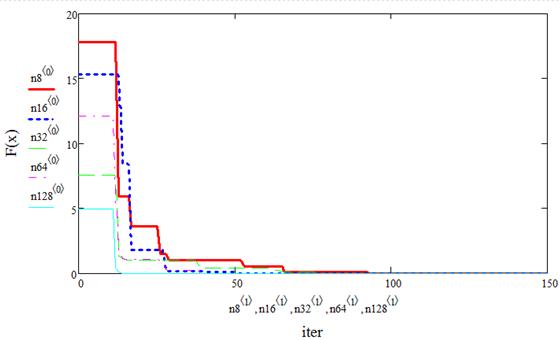
Рисунок 2. Скорость сходимости метода в зависимости от количества частиц в рое для функции Растригина (n=2)

Так как этот алгоритм является в большой степени алгоритмом случайного поиска, то увеличение размера роя и длительности работы алгоритма (количества итераций) очевидно повышает вероятность нахождения корректного решения задачи.

На рисунках 3 и 4 также приведены результаты работы алгоритма в зависимости от количества частиц в рое, но теперь уже для трехмерного пространства.

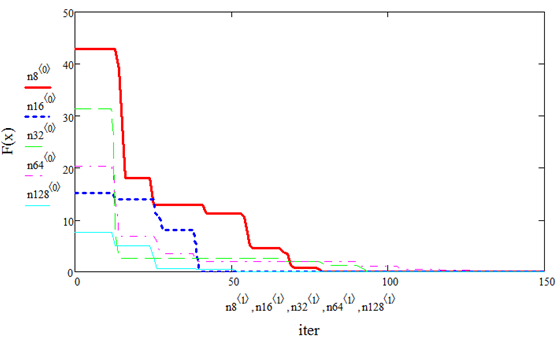
Рисунок 3. Скорость сходимости метода в зависимости от количества частиц в рое для сферической функции (n=3)

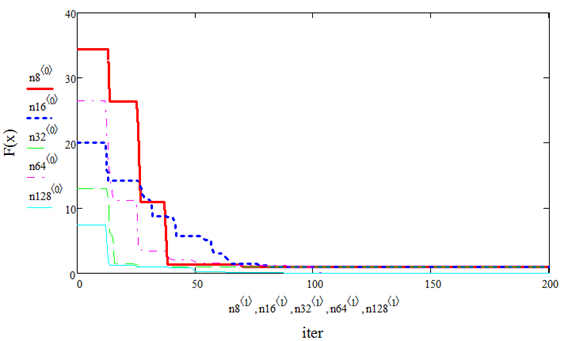
Рисунок 4. Скорость сходимости метода в зависимости от количества частиц в рое для функции Растригина (n=3)

Из последних четырёх графиков видно, как повышается точность решения с увеличением объема роя, но вместе с этим значительно возрастает время работы. В связи с этим было принято решение реализовать параллельный алгоритм на nVidia Cuda.

Большинство известных методов роя частиц являются последовательными. Параллельных методов известно немного, и все они появились после 2004 года. В работе рассмотрен метод, использующий островную модель параллелизма. Основная идея этого метода заключается в следующем: весь рой из N частиц делится на m островов (по количеству вычислительных устройств в системе) и частицы, принадлежащие каждому из островов, обрабатываются на своем графическом процессоре. После каждых k независимых итераций, острова обмениваются между собой лучшими частицами.

В работе было выполнено сравнительное исследование скорости сходимости параллельного и последовательного алгоритмов метода роя частиц для исследуемых функций, которое представлено на рисунках 5 и 6.

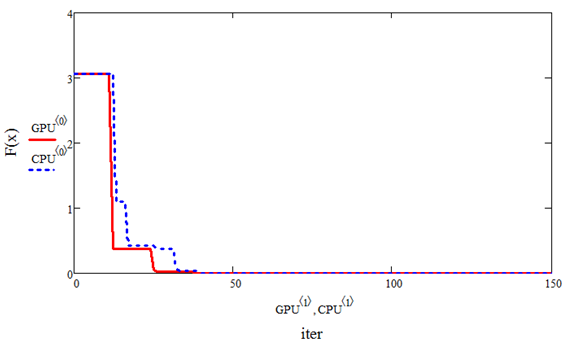
Рисунок 5. Скорость сходимости последовательного и параллельного методов роя частиц для сферической функции

Рисунок 6. Скорость сходимости последовательного и параллельного методов роя частиц для функции Растригина

Эффективность параллельных вычислений оценивается с помощью ускорения

,

где  — время решения задачи на однопроцессорном компьютере,  — аналогичное время при решении с использованием ГПУ. Подчеркнем, что под ускорением  в данном случае понимается повышение производительности вычислений при использовании ГПУ относительно производительности вычислений, производимых на однопроцессорном компьютере.

Таблица 1.

Сравнительный анализ параллельного и последовательного алгоритмов метода роя частиц

Проведенные исследования эффективности распараллеливания показали, что использование кластерных систем позволяет значительно снизить временные затраты (до 12 раз).

Наиболее перспективными направлениями дальнейших исследований в данном направлении следует считать теоретические исследования причин сходимости алгоритма роя частиц и связанных с этим вопросов из областей роевого интеллекта и теории хаоса, комбинирование различных модификаций алгоритма для решения сложных задач, рассмотрение алгоритма роя частиц как многоагентной вычислительной системы, а также исследование возможностей включения в него аналогов более сложных природных механизмов.

Список литературы:
1.    Алгоритм роя частиц — [Электронный ресурс] — Режим доступа. — URL:http://habrahabr.ru/post/105639/ (дата обращения 01.03.2014).
2.    Сандерс Д., Кэндрот Э. Технология CUDA в примерах: введение в программирование графических процессоров. Пер. с англ. — ДМК Пресс, 2011.
3.    J Kennedy, R Eberhart Particle swarm optimization. // Proceedings of IEEE International conference on Neural Networks. — 1995.
4.    Y. Shi, R. Eberhart A modified particle swarm optimizer» // The 1998 IEEE International Conference on Evolutionary Computation Proceedings, 1998 г.
5.    Weise T. Global Optimization Algorithms — Theory and Application: Ph.D. thesis / University of Kassel. — 2008.