РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ С ИСПОЛЬЗОВАНИЕМ МАТРИЦЫ И ЕЕ ДЕТЕРМИНАНТА

Статья посвящена матричному методу расчета электрических цепей. В ней рассмотрены основные теоретические понятия. На примере показана практичность и рациональность матричного метода в электротехнической инженерной практике. Также поднимаются вопросы взаимодействия математики и техники в целом.

В настоящее время трудно переоценить значение инженерной практики в современном мире науки и техники. Инженеры, используя огромные познания в математике, стимулируют научно-технический прогресс, результаты которого определяют поступательное развитие общества. Однако стоит отметить, что данное развитие имеет место, только при тесном взаимодействии математики и технической практики. Инженерное дело, как область интеллектуальной деятельности человека, не может быть реализовано без математического аппарата, на основе которого решаются основные научно-технические задачи. Соответственно и математика не имела бы возможности интенсивного развития, если бы не являлась основным инструментом в научно-технической деятельности. Это значит, что математика и инженерное дело взаимно дополняют друг друга. Таким образом, мы приходим к выводу, что современный инженер, воплощающий инновационные идеи, не может обойтись без уверенных знаний математики.

Например, инженер-электротехник для решения основных задач в своей области, в частности расчет параметров электрических цепей, использует уравнения Кирхгофа в матричной форме. В данном случае мы наблюдаем, как благодаря линейной алгебре и ее методам, значительно упрощается процесс длительных расчетов, а значит, увеличивается эффективность инженерной деятельности.

Рассмотрим базовую теорию. Матрица — это прямоугольная таблица чисел, в которой содержатся m строк (или n столбцов) идентичной длины.

или, сокращенно, , где  (т. е. ) — номер строки,  (т. е. ) — номер столбца.

Матрицу  называют матрицей размера  и обозначают . Числа , составляющие матрицу, называются ее элементами. Элементы, стоящие на диагонали, идущей из верхнего угла, образуют главную диагональ [3, c. 10]. Матрица, имеющая одинаковое количество строк и столбцов, называется квадратной.

Квадратной матрице  n-го порядка можно сопоставить число (или , или ), называемое ее детерминантом (или определителем), таким образом:

1. 

2. 

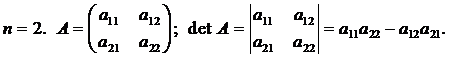
3. 

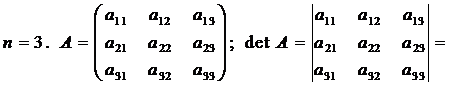
Минором некоторого элемента  детерминанта n-го порядка называется детерминант - го порядка, получившийся из исходного с помощью вычеркивания строки и столбца, на пересечении которых находится выбранный элемент.

Алгебраическим дополнением элемента , детерминанта называется минор, взятый со знаком «+», если сумма — четное число, и со знаком «—», если эта сумма нечетная. Обозначается как :  [3, с. 16]. Для расчета определителей 2-го и 3-го порядков используют следующие схемы (рисунок 1, рисунок 2):

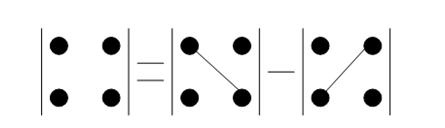
Рисунок 1. Порядок нахождения определителя 2-го порядка

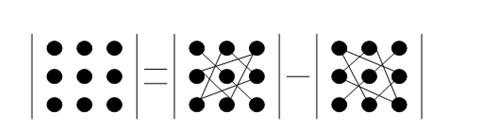
Рисунок 2. Порядок нахождения определителя 3-го порядка

Метод Крамера — способ решения систем линейных алгебраических уравнений с числом уравнений равным числу неизвестных с ненулевым главным детерминантом матрицы коэффициентов системы.

 (формула Крамера)

На примере продемонстрируем расчет электрической цепи с помощью данной теории.

Пример.

Задача:

Дана электрическая цепь (рисунок 3). Требуется определить токи в ветвях, с помощью законов Кирхгофа. Параметры элементов электрической цепи следующие: , ,, , ,

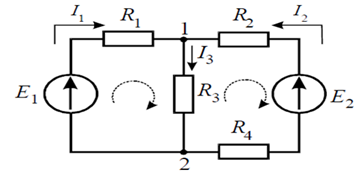
Рисунок 3. Схема электрической цепи

Решение:

Выбираем положительные направления искомых токов ветвей и обозначаем их на схеме.

Составляем уравнение, используя первый закон Кирхгофа для узла 1. Выбрав направления обходов контуров, записываем уравнения по второму закону Кирхгофа. В итоге имеем систему из трех уравнений:

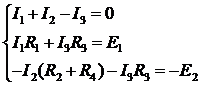
Решаем полученную систему по методу Крамера с помощью детерминантов:

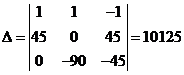
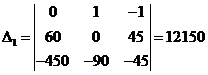
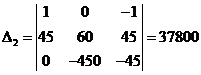
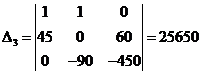
Находим значения токов по формуле Крамера:

Список литературы:
1.    Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. 9-е изд., перераб. и доп. — М: Высшая школа, 1996 г. — 638 с.
2.    Ланкастер П. Теория матриц. Издательство «Наука», М. ,1973, 280 с.
3.    Письменный Д.Т. Конспект лекций по высшей математике: полный курс / Д.Т. Письменный. — 4-е изд. — М.: Айрис-пресс, 2006. — 608 с.