АНАЛИЗ ПОВЕДЕНИЯ СТАЦИОНАРНОГО РАСПРЕДЕЛЕНИЯ СМО С БОЛЬШИМ ОБЪЕМОМ БУФЕРА

В последние годы во всем мире идет стремительная интеграция информационных и коммуникационных сервисов. Вследствие этого идет стремительный рост трафика и нагрузки на сетевое оборудование. Именно поэтому интересна проблема изучения вероятности отказа этого самого оборудования. Это позволит решать проблему целесообразности увеличения или уменьшения количества обрабатывающих устройств.

Такие обрабатывающие устройства можно описать с помощью математического аппарата теории систем массового обслуживания, что позволит исследовать их с нужной нам стороны.

Для реализации любой системы целесообразно моделирования, проверка ее эффективности в условиях, приближенных к условиям эксплуатации. Кроме того, моделирование предоставляет широкие возможности для более глубокого исследования и поиска закономерностей поведения.

Целью работы является исследование поведения вероятности отказа в зависимости от различных входных параметров.

Рассмотрим наиболее типичную модель в ТК, а именно M^X/M^Y/1 [3], то есть в любой момент времени поступает от 0 до Х заявок/пакетов/..., или обрабатывается так же от 0 до Y заявок/пакетов/... Такую СМО можно представить графом (рис. 1) (указаны переходы только для i-того узла, однако они аналогичны и для других):

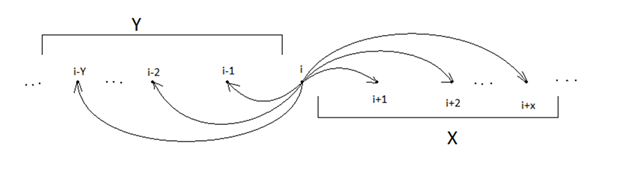
Рисунок 1 Граф переходов для i-го узла системы M^X/M^Y/1

Однако, в реальной жизни размер буфера не является бесконечным. Во многих ТК системах буфер является достаточно большим, по сравнению с X и Y, однако не бесконечным. Поэтому интересно, как себя ведет стационарное распределение на концах цепи (пустой буфер и полностью забитый) в зависимости от математического ожидания поступления и размера буфера.

Расчет вероятности СМО в отдельном случае.

Для примера, найдем стационарное распределение для такого случая: вероятность того что придет 2 заявки 0.4, 1 — 0.3, ни — 0.1, и одна обработается — 0.2. То есть:

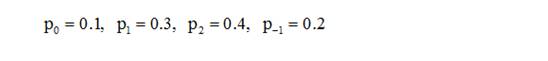(1)

Запишем рекуррентное уравнение [1]:

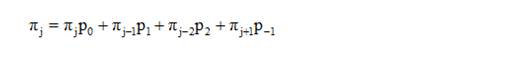(2)

Теперь из характеристического уравнения

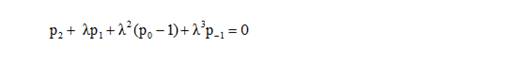(3)

Найдем параметры лямбда

                                   (4)

Тогда стационарное распределение будет выглядеть так:

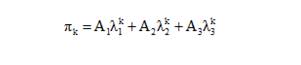                 (5)

Поскольку, при решении такого вида систем, значимыми будут только те уравнения, которые не имеют общей вид, то подставив (5) в (1) получим систему уравнений:

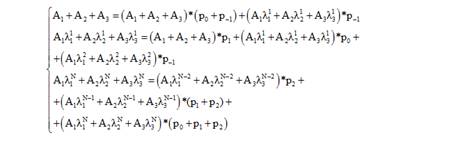(6)

Они все будут линейно зависимы, поэтому нужно одно заменить на [2]:

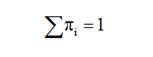                                     (7)

То есть

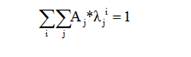                             (8)

Далее получаем такую систему:

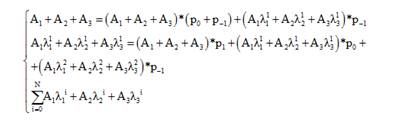(9)

Подставив значения и увидев формулу геометрической прогрессии в последнем уравнении:

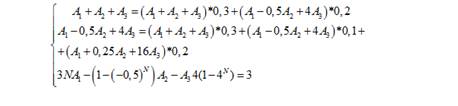(10)

Получим коэффициенты, зависящие от N:

                 (11)

Из формул для стационарного распределения можно увидеть, что для больших k наибольший вес имеет слагаемое с наибольшим лямбда (λ = 4), а для маленьких k значимыми также обнаруживаются и другие слагаемые (которые при больших N будут очень маленькие):

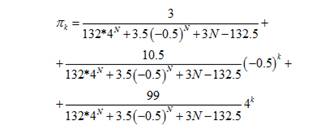                     (12)

Расчет вероятности СМО в противном случае.

Теперь возьмем вероятности поступления «зеркально» относительно р_0, то есть:

(13)

Аналогичным образом можно записать и решить характеристическое уравнение [1]. Коэффициенты в данном случае

                                             (14)

То есть мы видим, что они равны λ_i^-1 с предыдущего случая. В дальнейшем это было проверено и оказалось, что это условие выполняется всегда.

Теперь аналогично через систему из трех уравнений вычисляются коэффициенты А. Их значения:

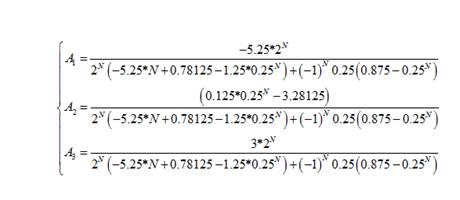(15)

То есть, можно увидеть, что эти коэффициенты А₁ и А₃ при больших значениях N стремятся к определенным константам. Поэтому [2]

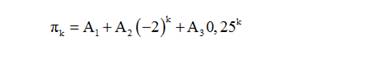(16)

с ростом k будет только уменьшаться.

Однако всегда ли это так? Возможно ли это использовать для упрощения расчета? Ведь, в реальных системах X и Y НЕ 2 и 1, а значительно больше.

Аналитический вывод формул.

Теперь абстрагируемся и представим, что максимально может приходит n заявок за раз, а обрабатываться — m [3]

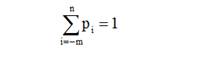                                  (17)

Так что можно сразу записать (1) и (5) в общем виде:

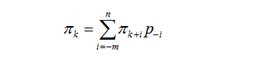                       (18)

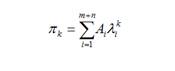                                          (19)

Тогда, аналогично вышесказанному, иметь такую систему уравнений:

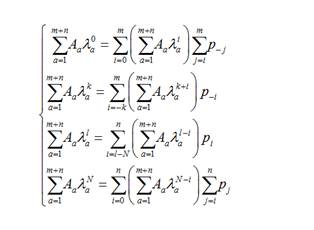                        (20)

Так же, уравнения в этой системе будут линейно зависимыми, следовательно заменим последнее на [3]

                                (21)

с подстановкой (19) и получим следующую систему

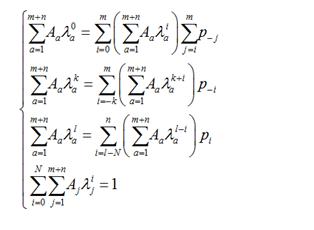              (22)

Можно увидеть, что количество уравнений зависит только от n и m; а также, что только последние n уравнений зависят от N. Таким образом эту систему относительно А можно записать в матричном виде

                       (23)

где: B и C — матрицы констант, которые теоретически можно легко рассчитать. Из этого можно предположить, что при достаточно больших N, выражения λ_N будут вести себя как в (1) по сравнению с самым λ _N, а следовательно коэффициенты А_i будут асимптотически зависеть только от этого λ_max и N. Также очень значимым является тот факт, что нам не приходится решать N уравнений. Благодаря тому, что мы воспользовались рекуррентными уравнениями, их осталось всего лишь m+n штук.

Соответственно, подведя итоги, можно сказать, что стационарное распределение будет иметь такой вид:

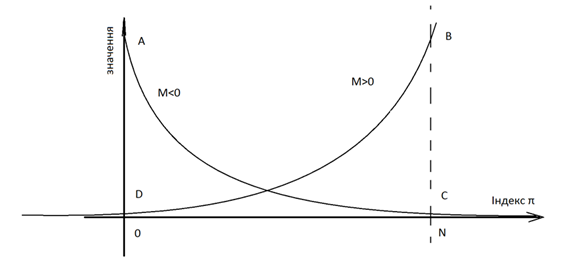
Рисунок 2 Распределение значений πі для случаев з положительным и отрицательным математическим ожиданием

То есть, для реальных систем, где нагрузка варьируется, можно подобрать интенсивность обработки и объем буфера (можно даже динамически) таким образом, чтоб обеспечить требуемый уровень отказоустойчивости системы.

Список литературы:
1.    Бочарова И.Е. Решение рекуррентных уравнений// Конспект лекций по курсу «Базовые алгоритмы обработки информации». — 2009. —[Электронный ресурс] — Режим доступа. — URL: http://k14.spb.ru/cm/uploads/105/014 (дата обращения 12.06.14).
2.    Тихонов В., Бакаев Ю. Статистическая теория радиотехнических устройств. М.: ВВИО, 1978.
3.    Adan I., Resing J. Queueing Theory: Ivo Adan and Jacques Resing. Eindhoven University of Technology. Department of Mathematics and Computing Science, 2001.