НОВЫЙ ПОДХОД К ПРОБЛЕМЕ ЭЛЕКТРОМАГНИТНОГО РАЗГОНА ОБЪЕКТОВ
Секция: 18. Электротехника

XIV Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
НОВЫЙ ПОДХОД К ПРОБЛЕМЕ ЭЛЕКТРОМАГНИТНОГО РАЗГОНА ОБЪЕКТОВ
В настоящее время вызывает интерес проблема ускорения объектов большой массы. Имеется в виду разгон объектов до скоростей, приближающихся к космическим. На сегодняшний день известны два способа электромагнитного разгона объектов: кондукционный и индукционный. Индукционный метод используется в системах магнитной левитации и в поездах на магнитной подушке. Кондукционный же себя зарекомендовал в военной сфере. Американские научно-исследовательские лаборатории, такие как General Atomics и ВМС США занимаются разработкой орудий с дульной энергией порядка 33 МДж. Уже имеются опытные образцы рельсотронов с дульной скоростью до 2,5 км/с.
Но у этих методов разгона есть свои недостатки. Кондукционный метод позволяет эффективно разгонять объекты значительной массы только до скоростей порядка 0,1 км/с. Индукционный же метод эффективно ускоряет только уже разогнанные объекты.
Цель нашей работы — разработать новую методику разгона объектов путем последовательного использования рельсотрона и линейного индукционного двигателя.
Решение проблемы возможно путем разумного сочетания кондукционного и индукционного принципов электромагнитного ускорения. При этом ускорение объектов на начальном этапе разгона (до 0,1 км×с-1), когда возможно надежное обеспечение электрического контакта между движущимся объектом и рельсами, предполагается осуществить по принципу (кондукционного) рельсотронного разгона, а на завершающей стадии ускорения (при скоростях, превышающих 0,1 км×с-1) применить индукционный принцип разгона.
РЕЛЬСОТРОННЫЕ УСКОРИТЕЛИ (ПЕРВАЯ СТУПЕНЬ РАЗГОНА).
Рельсотроны подразделяются на два типа: несегментированные и сегментированные. Для первых характерно то, что рельсы 1 (рисунок 1), вдоль которых происходит ускорение объекта 2, представляют собой единую конструкцию и находятся под напряжением источника питания в течение всего времени, пока объект находится в ускорителе, у вторых — рельс подразделяется на электрически несвязанные сегменты, причем каждый сегмент подключается к своему источнику питания по мере движения объекта по рельсу.
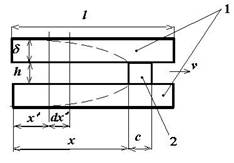
Рисунок 1. Несегментированный рельсотрон
Энергетическая эффективность несегментированных рельсотронов весьма низка, особенно при больших длинах рельса. Так, КПД разгона объектов массой 1000 кг от состояния покоя до скорости ![]() при изменении длины рельсотрона от 100 м до 1000 м находится в пределах от 0,07 до 0,03. В связи с отмеченным, целесообразно рассматривать сегментированные рельсотроны.
при изменении длины рельсотрона от 100 м до 1000 м находится в пределах от 0,07 до 0,03. В связи с отмеченным, целесообразно рассматривать сегментированные рельсотроны.
Для рельсотрона в данной работе исследуются следующие параметры:
· Энергия подводимая к ускорителю.
· Потери в рельсах.
· КПД.
Для выведения энергии подводимой от источника к ускорителю были приняты следующие допущения:
![]() — ускорение,
— ускорение,
![]() , (1)
, (1)
где: ![]() — сила трения о рельс;
— сила трения о рельс;
![]() — пропульсивная сила (тяги) рельсотрона;
— пропульсивная сила (тяги) рельсотрона;
![]() — ток, подведенный к сегменту.
— ток, подведенный к сегменту.
Тогда формула будет выглядеть так:
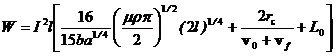 , (2)
, (2)
где: I — ток, подведенный к сегменту;
l — длина ускорителя;
b — ширина рельса;
a — ускорение;
ρ, μ — удельное сопротивление и магнитная проницаемость материала рельса;
rc — электрическое сопротивление объекта;
v0, vf — скорость объекта на входе и выходе ускорителя;
L0 — индуктивность рельсов на единицу длины.
Отличие от несегментированных рельсотронов будет состоять только в величине потерь в рельсах. Потери зависят от времени нахождения объекта на одном сегменте:
![]() (3)
(3)
таким образом
![]() . (4)
. (4)
Теперь мы можешь вывести КПД нашего ускорителя:
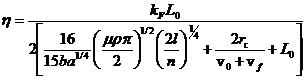 (5)
(5)
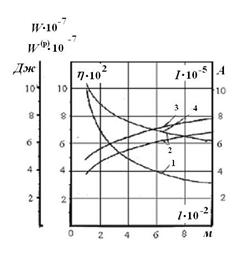
Рисунок 2. Результаты расчетов
На рисунке 2 приведены результаты расчетов тока (кривая 1), потерь в рельсе (кривая 2), потребляемой рельсотроном энергии (кривая 3) и его КПД (кривая 4) для сегментированных рельсотронов. Длина сегмента принималась одинаковой и равной 25 м. Расчеты выполнялись при ![]() м (ширина рельса),
м (ширина рельса), ![]() м (толщина рельса),
м (толщина рельса), ![]() м (расстояние между рельсами). Варьировалась длина рельсотрона.
м (расстояние между рельсами). Варьировалась длина рельсотрона.
Как можно увидеть из графика — КПД варьируется от 6 до 10 %, при токах порядка 10 кА.
ИНДУКЦИОННЫЕ УСКОРИТЕЛИ (ВТОРАЯ СТУПЕНЬ РАЗГОНА).
Для индукционного ускорителя в данной работе исследуются следующие параметры:
· Пропульсивная сила ускорителя.
· Длина ускорителя.
· Закон управления амплитудой напряжения.
При этом должно обеспечиваться постоянное ускорение объекта на всей длине разгона, независимо от силы сопротивления. Т. е. должна решаться проблема минимизации длины ускорителя и времени достижения необходимой скорости объектом на выходе из ускорителя.
Ускорение с непрерывным изменением синхронной скорости.
Данный ускоритель представляет собой трехфазный линейный индукционный двигатель (ЛИД). Для регулирования пропульсивной силы используется частотное регулирование при постоянной длине волны поля. Эффекты, обусловленные ограниченностью размеров ускоряемого объекта, учитываются соответствующими вычислениями его электромагнитных параметров — активного r2 и индуктивного х2 сопротивлений и индуктивного сопротивления хт взаимной индукции между объектовом и индуктором.
Воспользовавшись известными в теории обычных индукционных машин соотношениями можно вывести формулу пропульсивной силы:
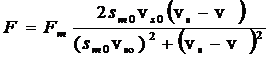 , (6)
, (6)
где: sm0 и vs0 — значения sm и vs при базисной частоте;
vs и v — текущие значения синхронной скорости и скорости движения объекта.
Для нас представляет интерес разгон объекта, при котором разность текущей и синхронной скорости не зависит от частоты питающего напряжения и равна ![]() :
:
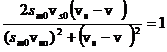 (7)
(7)
Таким образом, ускоритель развивает максимальную силу. Однако Fm зависит от частоты. Поэтому для оптимального разгона применим еще одно условие:
![]() , (8)
, (8)
где: f0 и U0 — базисные значения частоты и напряжения.
Тогда уравнение примет вид:
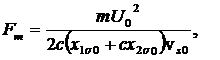 (9)
(9)
где: x1s0 и x2s0 — значения сопротивлений х1s и x2s при частоте f0.
Имея в виду одномерное движение объекта, можно выразить длину ускорителя:
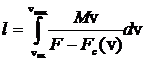 , (10)
, (10)
где: ![]() и vвых — скорости объекта на входе и выходе ускорителя.
и vвых — скорости объекта на входе и выходе ускорителя.
Но поскольку мы живем в реальном мире, то движению нашего объекта будет препятствовать сила сопротивления, которую возьмем произвольной функцией от скорости объекта. Тогда сила развиваемая ускорителем, необходимая для подавления силы сопротивления будет равна:
F=Fm0+Fc(v) (11)
Теперь закон управления амплитудой напряжения можно представить в виде
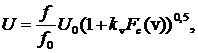 (12)
(12)
где: kv — коэффициент управления по параметру v
Ускорение с дискретным изменением синхронной скорости.
Теперь рассмотрим ускоритель с непрерывным изменением синхронной скорости, то есть Линейный двигатель, состоящий из некоторого числа участков (сегментов), каждому из которых соответствует своя постоянная синхронная скорость.
Основные исследуемые параметры:
· Пропульсивная сила сегмента.
· Длина сегмента.
Если рассматривать kv как переменную величину, зависящую от синхронной скорости и скорости объекта, то при условии
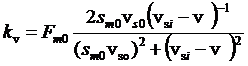 (13)
(13)
где: I – номер сегмента
Пропульсивная сила, развиваемая ускорителем на i-м сегменте
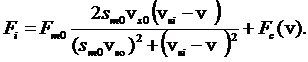 (14)
(14)
Используя уравнение для одномерного движения (10) мы преобразовываем его согласно предыдущим уравнениям
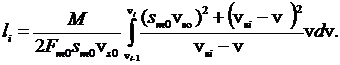
В заключение приведем некоторые результаты расчета, относящиеся к сегментированному индукционному ускорителю с n=11. Уравнения решались методом Ньютона. Были получены значения синхронных скоростей vs на всех сегментах и n-1 скоростей v объекта на границах сегментов при скоростях vвх=0,1 км×с-1 и vвых=1 км×с-1. В расчетах предполагалось, что sm0vs0=11,1; 25; 43; 67; 100.
На рисунке 3 приведены графики синхронной скорости (горизонтальные отрезки 1) и скорости объекта (кривая 2) для случая ![]() . Расчеты показали, что независимо от значения
. Расчеты показали, что независимо от значения ![]() скорость объекта в конце каждого сегмента вплотную приближается к синхронной скорости на этом сегменте.
скорость объекта в конце каждого сегмента вплотную приближается к синхронной скорости на этом сегменте.
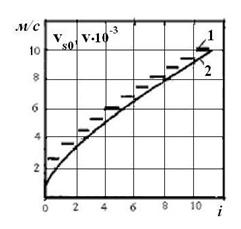
Рисунок 3. График синхронной скорости и скорости движения объекта
Вывод.
1. Одним из наиболее эффективных путей повышения КПД рельсовых ускорителей является разделение рельса на отдельные электрически не связанные участки (сегменты) и питание в любом момент времени только одного сегмента, в пределах которого находится ускоряемый объект. Этот путь при рациональном выборе полной длины ускорителя и длины отдельных сегментов вместе с регенерацией энергии магнитного поля рельса позволяет получить приемлемые значения КПД рельсотрона, порядка 15—20 %.
2. Для достижения минимальной длины индукционного ускорителя с непрерывным изменением синхронной скорости, а, следовательно, и минимального времени разгона объекта необходимо управление частотой и амплитудой питающего напряжения по законам (12).
3. На минимальную длину сегментированного ускорителя заметное влияние оказывает параметр sm0vs0. Это влияние тем значительнее, чем больше выходная скорость ускорителя. С точки зрения минимизации длины ускорителя желательно, чтобы параметр sm0vs0 был возможно больше.
Список литературы:
1. Вольдек А.И. Электрические машины. Л.: Энергия, 1974. 839 с.
2. Ким К.К. Регулирование питающего напряжения индукционного ускорителя при минимизации его длины и времени разгона // Электричество, № 11, 1990. С. 59—62.
3. Ким К.К. Электромагнитное разгонное устройство // Сборник трудов Самарского политехнического института «Специальные типы электрических машин». Самара. 1991. 6 с.
4. Deadrick P.J., Hawke R.S., Sendder J.D. Madrac-a railgun simulation program // IEEE Transactions on Magnetics. 1982. ¾ Vol. MAG-18. ¾ № 1. ¾ Р. 94—104.
5. Onuki T., Laithwaite E.R. Problem of minimizing induction launchers length // Proc. of the Institute of Electrical Engineers. ¾ 1971. ¾ Vol. 118. ¾ № 2





