Экспериментальная проверка достоверности математической модели арочного двухслойного покрытия из профилированного тонкостенного проката

Рассмотрим единичной ширины арочный профиль радиусом r и заданными геометрическими характеристиками, имеющий опоры по концам и на который действует поперечная q_y и продольная сжимающая или растягивающая нагрузка q_z, ориентированные в плоскости арки. При этом сосредоточенные нагрузки будем представлять в виде распределенных на малых дугах dS = r×dj. Величина dj задается из конструктивных соображений.

При построении математической модели будем пренебрегать взаимным влиянием арочных заготовок друг на друга под нагрузкой (нагрузка равномерно распределена вдоль покрытия; покрытие не имеет торцовых ограждающих конструкций) [1; 2].

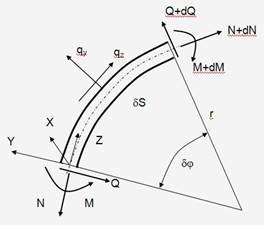
Рисунок 1. Равновесие бесконечно малого элемента дуги

Таким образом, три уравнения равновесия, два геометрических и физическое соотношения, образуют полную математическую модель кругового стержня постоянной кривизны, нагруженного внешними силами заданной интенсивности:

 N’ = -Q-q_z×r,

Q’ =N-q_y×r,

M’ = Q×r,

W’ = -V,

V’ = W - r×Dj,

Dj’ = .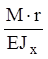

Для определения шести начальных параметров (Q_o = Q_y(φ = 0), N_o = N(φ = 0), M_o = M(φ = 0), V_o = V(φ = 0), W_o = W(φ = 0), Dj_o = Δφ(φ = 0) в конкретной задаче всегда формулируются достаточное количество граничных условий, так как при любом закреплении концов стержня, на каждом известны три условия:

·     жесткое закрепление v = 0, w = 0, j = 0;

·     шарнирно-неподвижное закрепление M = 0, v = 0, w = 0;

·     шарнирно-подвижное закрепление M = 0, v = 0, N = 0;

·     свободный конец M = 0, Q_y = 0, N = 0 и т.д.

Аналитическое решение полученной системы шести дифференциальных уравнений получено только при нагрузках постоянной интенсивности и постоянном сечении стержня. Даже в этих простых частных случаях нагружения решение представляет собой достаточно громоздкие кусочно-непрерывные функции, анализ которых проводится после построения их графиков (эпюр). С введением нагрузки, изменяющейся по заданному закону или переменном моменте инерции сечения, решение системы уравнений состояния в аналитическом виде получить невозможно [1; 2].

Для проверки достоверности математической модели арочного двухслойного покрытия провели эксперимент.

В качестве испытываемого образца был смонтирован фрагмент арочного двухслойного покрытия из профиля Н60, толщина материала 0,9 мм (сталь марки 08 ЮУ 2) с длиной пролета 18 м, стрелой 3,5 м и шириной 2,5 м., составленный из трех арочных заготовок (рис. 2). В качестве термопрофиля использовано девять единиц трапециевидного профиля, установленных с шагом 2000 мм.

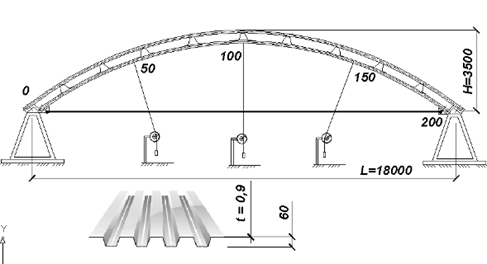
Рисунок 2. Схема и основные геометрические размеры экспериментального двухслойного арочного покрытия

Нижний и верхний слои покрытия закреплены к опорам из прокатных швелеров № 22 с помощью болтов М16, установленных через жесткие шайбы в каждую волну профилей. Термопрофили связывают верхний и нижний слои посредством стандартных саморезов ø4,3 мм. Саморезы установлены в каждую волну арочного профиля – в нижнем слое в верхнюю полку, в верхнем слое в нижнюю полку.

Для проверки адекватности исследуемой математической модели арочного покрытия проводилось нагружение покрытия системами сосредоточенных нагрузок с измерением радиальных перемещений прогибомерами системы Максимова в сечениях 50, 100, 150 единиц (вся длина арки составляет 200 единиц или 200 шагов интегрирования).

Нагружение производилось ступенчато с последующей ступенчатой разгрузкой, производимой в обратном порядке. Точность измерения перемещений составляла 0,01 мм (цена деления индикатора часового типа ИЧ – 100).

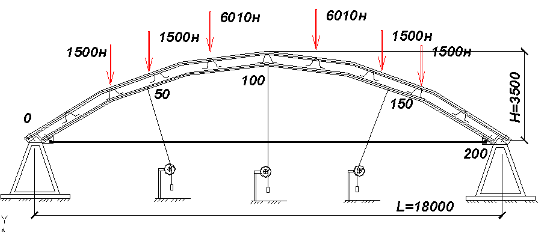
Рисунок 3. Схема нагружения

Результаты испытаний приведены в таблице 1.

Таблица 1.

Результаты испытаний

Максимальная суммарная нагрузка в эксперименте превышала 40 Кн (включая собственный вес арки). Максимальные расчетные нормальные напряжения составляли 135 МПа. Значительные расхождения ряда экспериментальных и расчетных значений перемещений (таблица 1) следует отнести на накопленные неточности, связанные с:

·     погрешностями сборки и установки конструкции в целом;

·     погрешностями взвешивания грузов;

·     погрешностями координат установки грузов;

·     погрешностями геометрии арки в целом и рядом других неточностей.

В целом эксперимент показал удовлетворительную для инженерных расчетов точность вычисления прогибов арочного покрытия. Это дает право использовать данную математическую модель арочного покрытия для проведения вариантных расчетов с целью поиска оптимальных соотношений геометрических параметров арок применительно к конкретным внешним нагрузкам.