Представление и обработка образов конструктивных элементов
Секция: Технические науки

XLVIII Студенческая международная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
Представление и обработка образов конструктивных элементов
На многих современных предприятиях используются системы автоматизированного проектирования (САПР). Функции и возможности данных систем проектирования могут быть самыми разными. По сравнению с историей развития вычислительной техники история развития автоматизированных систем очень коротка, она не насчитывает и пятидесяти лет. При этом без этих систем компьютеры никогда бы не стали тем, чем они являются сейчас – орудием труда миллионов специалистов, занятых проектированием в самых разных областях.
САПР – системы автоматизированного проектирования, использующие различные графические ядра для построения геометрии. В настоящее время основной проблемой, с которой сталкиваются группы разработчиков, является отсутствие возможности полноценного обмена результатами проектной деятельности при использовании различных систем автоматизированного проектирования. Данную проблему устранила бы возможность восстановления способа построения экспортируемого объекта.
Конструктивный элемент (КЭ) — основная единица проектирования в современных САПР, которая представляет собой элемент, задающий форму изделия. Путем изменения параметров КЭ осуществляется изменение формы проектируемого изделия. Важно подчеркнуть, что конструктивный элемент – это не одна единственная деталь конечной формы. Он может обладать множеством вариаций, но при этом не переставать быть тем же конструктивным элементом.
Как простейший пример для понимания можно привезти винт, имеющий различные варианты шляпки: крестообразную, плоскую или «звездочку».
Для граничного представления объекта основными являются понятия геометрии и топологии. Так, под геометрией понимается математическое описание формы, а под топологией – структура данных, позволяющая связывать геометрические объекты в систему. Таким образом, топологию можно представить в виде графа, иллюстрирующего связь между геометрическими примитивами, объединенными определенными ограничениями (рис.1). Применительно к построению конструктивных элементов такой граф будет содержать в себе множество решающих деревьев, каждое из которых будет соответствовать последовательности построения конкретного образа конструктивного элемента. [1][3]
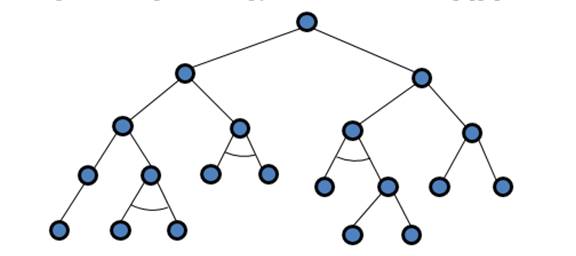
Рисунок 1. Одна из возможных топологических структур
Рассмотрим конструктивный элемент – фасонный резец. Построение детали имеет формульное представление, и итоговый вариант зависит от различных условий (форма резца, используемый металл и т.д.). Получение модели состоит из нескольких шагов:
1. Конкретизация задачи: формулировка, ограничения
2. Геометрическая реализация, включающая создание дерева построения (рис.2)
3. Создание расширенного дерева: добавление к дереву построения конструктивных особенностей, которые могут быть заданы формульно или таблично (рис.3)
4. Построение обобщенного дерева, содержащего все возможные варианты построения конструктивного элемента
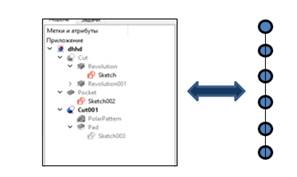
Рисунок 2. Дерево построения

Рисунок 3. Расширенное дерево
На последнем этапе построения модели реализуется построение обобщенного дерева (рис.4). Его отличие от расширенного дерева состоит в поиске оптимального пути построения конструктивного элемента с учетом ограничений и упрощения геометрической реализации. Данный путь выделен на рисунке 4 жирной линией и называется решающим деревом. [2][4][5]
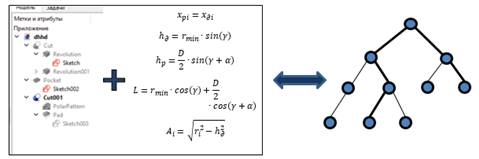
Рисунок 4. Обобщенное дерево
Применительно к фасонному резцу, используемому для рассмотрения модели, выбор различных решающих деревьев может привести к построению круглого или призматического резца, что имеет принципиальную разницу для его использования на станках с различными креплениями. Однако оба способа получения должны быть отражены в модели, так как являются альтернативами одного конструктивного элемента (рис. 5.).
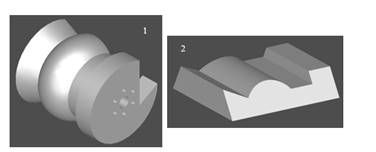
Рисунок 5. 1 – круглый фасонный резец; 2 - призматический
Любой процесс построения конструктивного элемента является сложной системой, которую можно поэтапно разбить на множество простых задач. Для наглядного представления таких систем удобно использовать дерево состояний. Представим дерево состояний для резца в виде И/ИЛИ графа (рис. 6). Данный граф является полной геометрической иллюстрацией модели.
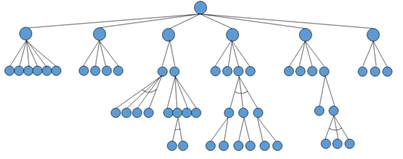
Рисунок 6. И/ИЛИ граф фасонного резца
С помощью алгоритмов поиска в глубину и ширину на И/ИЛИ графе были определены все возможные варианты решающих деревьев для получения фасонного резца. Метод ветвей и границ в данном случае не применим, так как требуется найти не наилучший, а все возможные варианты построения, а в силу специфики задачи вершины и ветви не имеют оценок. Поиск решающих деревьев в данном случае занял рассмотрение 38 ветвей с проверкой на каждом шаге разрешимости предыдущих вершин для каждой ветви.
Также следует сказать, что данный способ отыскания решающих деревьев будет всегда допустим и приводить к оптимальному решающему дереву при условии правильности составления обобщенного И/ИЛИ дерева.
На рис.7 представлен И/ИЛИ граф фасонного резца с решающими деревьями.

Рисунок 7. И/ИЛИ граф фасонного резца
Однако передавать сам граф нет возможности. К тому же, это нецелесообразно. Необходимо каким-либо образом предоставить математическое описание графа по которому можно было бы определить все множество вариантов построения конструктивного элемента. Необходимо получить прямое соответствие между техническим заданием, которое отражает всю полноту картины построения, и конструктивным элементов в целом, а не только его конкретным образом. Для этого переменные в формуле должны каким-либо образом описывать ветвления графа. То есть должны быть уже не единичным значением, а целой структурой. Данная структура должна полностью описывать конкретное ветвление со всеми его характеристиками. Для этого разработана система (1), которая в полной мере описывает конструктивный элемент с геометрической и параметрической точки зрения.
 (1)
(1)
Векторы γi, αi, Di, ri – векторы значений, определяемые для каждого конкретного фасонного резца индивидуально из таблиц технического задания (Приложение 1).
Векторы hδi, hpi, Li, Ai – векторы промежуточных расчетных значений.
Векторы Xi, Ri – результирующие векторы значений, определяющих основные параметры фасонного резца.
Разработанная модель позволяет в полной мере описывать способ построения конструктивного элемента, учитывая все аспекты построения: геометрию, конструктивные особенности в их математическом представлении (формулы, таблицы данных и т. д.) и множество путей решений получения различных образов одного конструктивного элемента. Полученная модель рассматривается как алгоритм для написания программного обеспечения, позволяющего осуществить автоматическую реализацию концепции модели при подключении к специализированным средствам (САПР).





