ИСПОЛЬЗОВАНИЕ ТРАНСЛИРУЮЩИХ ГРАММАТИК ПРИ ПРОЕКТИРОВАНИИ ТРАНСЛЯТОРА
Секция: 3. Информационные технологии

XVI Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
ИСПОЛЬЗОВАНИЕ ТРАНСЛИРУЮЩИХ ГРАММАТИК ПРИ ПРОЕКТИРОВАНИИ ТРАНСЛЯТОРА
В настоящее время в мире насчитывается свыше тысячи языков программирования. Однако язык останется мертворожденным, если он не будет реализован на ЭВМ. Реализация языка означает разработку и использование специальной программы — транслятора, «понимающей» тексты на этом языке и осуществляющей процесс трансляции, то есть перевода исходного текста программы в исполнительный файл или программу на другом языке программирования.
Примерами таких языков могут служить системы запросов, языки управления некими объектами, различные препроцессоры, языки систем автоматизированного проектирования и т. д.
Существование различных языков программирования зачастую обязано возникающей актуальной до настоящего времени задача представления, то есть описания языка программирования, значимость которой особенна тем, что любой подобного рода формализм позволяет перейти на более высокий уровень абстракции, охватывающий уже гораздо больше конкретных вариантов, т. е. более высокий уровень абстракции позволяет решать более сложные задачи в достаточно обширных областях.
Традиционно описание языка состоит из описания его лексических свойств, описывающих правила составления отдельных слов языка или лексем, синтаксических свойств, описывающих правила составления из лексем отдельных предложений, принадлежащих описываемому языку и семантических свойств, определяющих корректность совокупности предложений языка с точки зрения смысла. Для первых двух составляющих разработаны соответствующие формализмы. Существуют методы и для описания семантики, но их формальное применение при разработке транслятора представляется достаточно затруднительным [1].
Механизм описания формального языка основан на принципах предварительного метапрограммирования, представляющего собой вид программирования, связанный с созданием программ, которые порождают другие программы как результат своей работы. В частности при описании формальных языков языком метапрограммирования является форма Бэкуса-Наура или формальная система описания синтаксиса, в которой одни синтаксические категории последовательно определяются через другие.
С помощью подобной иерархической парадигмы метапрограммирования можно описывать довольно сложные синтаксические структуры и языки программирования.
Однако при более специализированных взаимосвязях сложных синтаксических конструкций, описать которые с помощью подобного рода грамматик невозможно на практике их расширяют понятиями атрибутных грамматики, которые позволяют наследовать атрибуты для вложенных грамматических правил, позволяя тем самым осуществлять, например, проверку на соответствие типов.
Зачастую сам процесс трансляции осуществляется в три этапа: лексический и синтаксический анализ и непосредственно трансляция программы в целевую форму. При этом также существует множество подходов реализации данного процесса, одним из которых является использование транслирующих грамматик, которые в отличии от обычных грамматик включают в свой состав так называемые символы действия. При этом процесс синтаксического анализа объединяется вместе с процессом трансляции: то есть при проверке входной строки на её соответствие синтаксису при встрече в искомой грамматике символа действия транслятор выполняет ассоциированное с ним действие, вследствие чего результатом работы транслятора является последовательность актов, каждый из которых способен определенным образом конфигурировать выходную строку [1; 3].
С помощью данного подхода можно организовать перевод математических выражений из инфиксной формы в постфиксную, являющимся предметом настоящего исследования.
Постфиксная запись или обратная польская нотация (ОПН) — форма записи математических выражений, предложенная польским математиком Яном Лукасевичем в которой операнды расположены перед знаками операций [3].
Подобный стиль записи математических выражений является наиболее оптимальным при автоматическом вычислении значения выражения с использованием стековой архитектуры. При этом порядок вычисления элементарен: если следующий символ в выражении — число, то оно заносится на вершину стека, если это операция, то из стека выталкиваются два верхних элемента, над которыми эта операция выполняется, а результат снова заносится на вершину стека.
В структуру синтаксического блока некоторых компиляторов включается специальный блок перевода арифметических выражений в постфиксную форму. Реализацию поставленной задачи реализации подобного рода предварительного транслирующего блока принято осуществлять с проектирования целевой транслирующей грамматики, лежащей в его основе с использованием формы Бэкуса-Наура, которая в результате принимает следующий вид, где ε — пустой символ.
<S> → <Id>{Id}<Spaces>={=}<Spaces>< Expression ><Spaces>;{PopAllSign}{;}<Spaces><S> | ε
<Spaces> → <Space><Spaces> | ε
<Space> → | \r | \n | \t
<Id> → <FirstChar><Chars>
<FirstChar> → _ | a | b | c | … | z | A | B | C | … | Z
<Chars> → <Char><Chars> | ε
<Char> → <FirstChar> | <Digit>
<Expression> → <Operand><Spaces><Boundary>
<Boundary> → <Sign>{TryPopSign}<Spaces><Expression> | Ԑ
<Sign> → + | – | * | /
<Operand> → ({PushBraket}<Spaces><Expression><Spaces>){PopToBracket} |
<Number>{<Number>} | <Id>{<Id>}
<Number> → <Digits><FloatDigits>
<FloatDigits> → .<Digits> | ε
<Digits> → <Digit><Digits> | ε
<Digit> → 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
В представленной грамматике используется ряд операционных нетерминальных символов, обеспечивающих процесс трансляции входной строки в результирующую строку в постфиксной форме в ходе синтаксического анализа.
Операционный нетерминал {TryPopSign} обозначает операцию, выполняющую попытку выталкивания предыдущего символа арифметической операции из стека операций, при этом производится сравнивание предыдущей и текущей операции и первая выталкивается на выходную ленту только в случае её равенства или старшинства по сравнению с текущей. Далее в любом исходе текущий символ операции вталкивается в стек операций, ожидая следующей проверки.
Операционный нетерминал {PushBraket} обозначает операцию вталкивания в операционный стек открывающей скобки, что позволяет выделять выражения, объединенные в скобки.
Операционный нетерминал {PopToBracket} обозначает завершение выражения объединенного в скобку и выполняет выталкивание всех операций из операционного стека в выходную ленту в порядке их размещения, пока не встретится соответствующая открывающая скобка.
Операционный символ {PopAllSign} обозначает завершение всего выражения и выполняет выталкивание на выходную ленту оставшихся операций.
Остальные операционные символы {Id}, {=}, {;}, {<Number>} и {<Id>} просто отображают в выходную строку предшествующие лексемы чисел, идентификаторов и служебных символов на выходную ленту.
В качестве практической реализации представленного транслятора математических выражений выступает разработанное в рамках данного исследования приложение на языке C# с использованием библиотеки WPF [2].
Процесс трансляции осуществляется в виде двухступенчатого конвейера, при котором каждая ступень передает управление следующей после полного анализа принятых данных, а полученные результаты передаются на вход следующего анализатора.
С помощью представленной организации транслятора можно разделить идентификацию ошибок по их принадлежности к классу лексических или синтаксических ошибок, которые в окне ввода и логе ошибок отображаются соответствующим образом, пример которого представлен на рисунке 1.
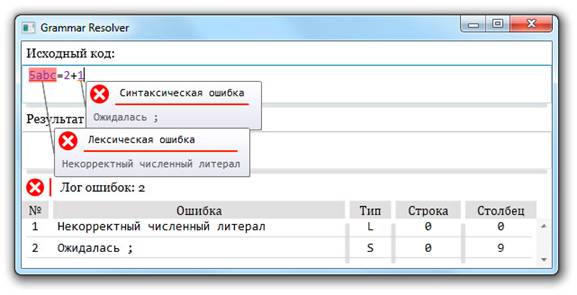
Рисунок 1. Пример обработки ошибок
По объективным причинам при наличии ошибок нижнего или верхнего уровня процесс трансляции результата работы не осуществляется, а возвращаются только списки ошибок.
Результат корректной трансляции представлен на рисунке 2.
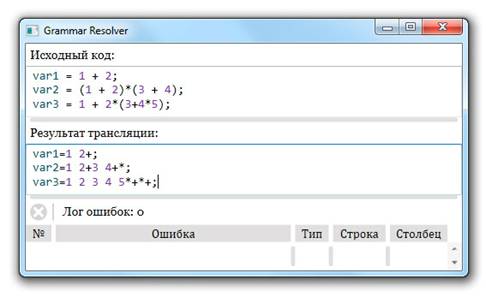
Рисунок 2. Пример корректной трансляции
В качестве заключения нужно сказать, что исследования, проводимые в области теории языков программирования, методов трансляции, разработки новых методик формализации и абстрагирования от оборудования являются достаточно востребованными, так как сложность современных программных продуктов, систем автоматизированного управления растет и их применение расширяется, соответственно существует потребность в средствах эффективной, качественной и быстрой программной разработке.
Список литературы:
1. Кревский И.Г., Селиверстов М.Н., Григорьева К.В. Формальные языки, грамматики и основы построения трансляторов: Учебное пособие / Под ред. А.М. Бершадского — Пенза: Издательство ПГУ, 2002. — 124 с.
2. Мэтью Мак-Дональд. Pro WPF in C# 2010: Windows Presentation Foundation in .NET 4. — Москва, Санкт-Петербург, Киев: Издательский дом «Вильямс», 2011. — 1024 с.
3. Свердлов С.3. Языки программирования и методы трансляции: Учебное пособие. — СПб.: Питер, 2007. — 638 с.





