ИНЖЕНЕРНАЯ ТЕОРИЯ РАСЧЕТА ГЕОМЕТРИЧЕСКИХ И СИЛОВЫХ ПАРАМЕТРОВ ИЗГОТОВЛЕНИЯ ГНУТЫХ ЭЛЕМЕНТОВ ХУДОЖЕСТВЕННОЙ КОВКИ

Наиболее распространенными декоративными элементами в художественной ковке, по-видимому, являются волюты. В своей основе они восходят к ионическому стилю, представляя собой наиболее характерный элемент капителей ионических колонн. Ковка волюты осуществляется свободным способом, при этом получение правильной спиральной формы целиком зависит от мастерства кузнеца-художника.

В общем случае изготовление волюты заключается в нагреве прутка с последующей законцовкой на наковальне. Далее на ребре или роге наковальни оформляется наиболее крутой завиток. После этого снова нагревают заготовку на возможно большую длину и с помощью спиральной оправки куют спираль (рис. 1) [1; 2].

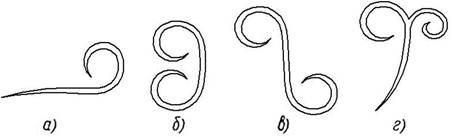
Рисунок 1. Форма волют: а — односторонняя; б — двусторонняя; в — двусторонняя с обратной закруткой; г — двусторонняя с разветвлением от одного прутка

При необходимости изготовления большого числа одинаковых спиралей, обычно делается шаблон (кондуктор), таким образом, чтобы в его контуры вписывался каждый оборот спирали и толщина заготовки, предназначенной для ее изготовления.

Однако при этом, следует принимать во внимание, что формообразующие элементы рабочего инструмента (штампа, матрицы; кондуктора и др.) должны иметь кривизну, отличную от кривизны изгибаемой детали на величину пружинения (увеличение радиуса кривизны после разгрузки). Ввиду этого угол загиба должен быть больше заданного на величину пружинения.

Следовательно, вопрос сводится к решению обратной технологической задачи — нахождению кривизны и угла загиба, на которые необходимо произвести деформацию, с тем, чтобы после пружинения получить их значение равным заданному.

Рассмотрим формообразование волюты, закрученной из квадратного прутка со стороной  мм с переменным радиусом кривизны, полученную по закону архимедовой спирали (рис. 2).

Создаваемый при этом радиус кривизны нейтрального слоя, будет определяться соответствующими участками волюты. Так, радиус кривизны нейтрального слоя первого участка волюты (отсчет от центра спирали и против часовой стрелки)

 мм

Относительный радиус кривизны нейтрального слоя [3]

,

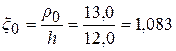где:  мм — высота изгибаемого прутка.

Следует отметить, что остаточная кривизна материала при изгибе определяется величиной упруго-пластических деформаций, связь которых с напряжениями в упругой зоне принимается линейной , а в пластической зоне — степенной

,                                                              (1)

где:  МПа — модуль нормальной упругости материала.

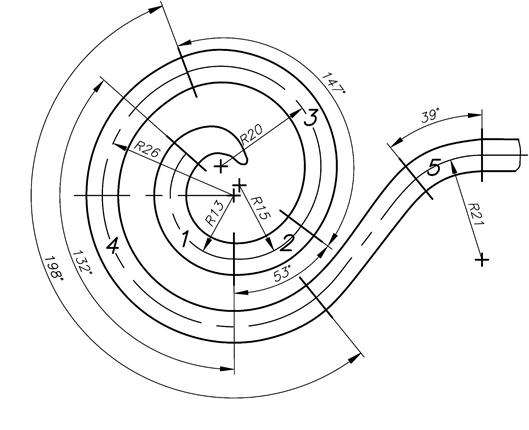
Рисунок 2. Построение срединной линии волюты

Константы K и n удобно представить через основные механические свойства, известные по стандартным испытаниям металла на растяжение. Подчиняя зависимость (1) условию прохождения аппроксимирующей кривой через точки условного предела текучести (, ) и предела прочности (, ) истинной кривой упрочнения, находим константы аппроксимирующей степенной кривой упрочнения в пластической зоне

; .

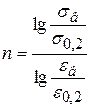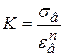Очевидно, физическая зависимость (1) учитывает природу, структуру, термическое состояние и другие физико-механические факторы, так как они отражаются на пределах текучести и пластичности материала, через которые выражены константы функциональной зависимости σ — ε.

В теории обработки металлов давлением, с целью упрощения расчетов, напряженное состояние материала в очаге деформации принято разделять на объемное и плоское.

При изгибе на большие радиусы кривизны  взаимное нажатие волокон друг на друга пренебрежимо мало, напряженное состояние можно принять плоским, тогда приведенный модуль упрочнения

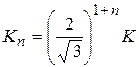.                                       (2)

В случае малого радиуса кривизны, напряженное состояние будет объемным и можно принять .

Переход линейной зависимости σ — ε в степенную на истинной кривой упрочнения происходит при относительной деформации (рис. 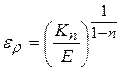3).

,                                          (3)

определяющей положение границ зон упругой и пластической деформации по высоте сечения в зависимости от радиуса кривизны.

Рисунок 3. Аппроксимация истинной (1) диаграммы σ — ε линейной функцией в упругой области и степенной (2) в пластической области деформаций

В качестве материала волюты принимаем широко используемую в художественной ковке сталь Ст. 10 со следующими константами кривой упрочнения (при гибке в холодном состоянии)

 МПа; .

Так как относительный радиус кривизны , напряженное состояние в материале считается объемным, тогда приведенный модуль упрочнения (2)

 МПа.

Деформация, определяющая разделение сечения на упругую и пластическую зоны (3)

.

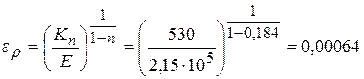Соответствующее этому значению положение границ зон упругой и пластической деформации по высоте сечения зависит от радиуса кривизны нейтрального слоя и относительно последнего определяется ординатой (рис. 4)

 мм

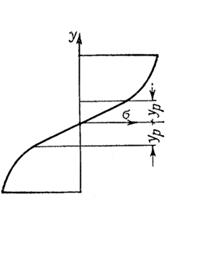
Рисунок 4. Эпюра упруго-пластического изгиба

Коэффициент, характеризующий относительную величину упругой зоны по высоте сечения (зависит от создаваемой кривизны нейтральной линии)

,

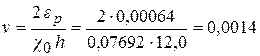где:  — кривизна в сечении изогнутого элемента

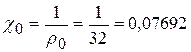 мм^-1.

Относительная кривизна нейтральной линии после пружинения (4)

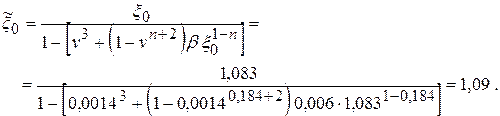
где: β — постоянный для каждого металла коэффициент, выражаемый через его механические свойства

.

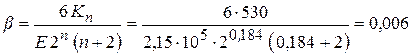Согласно теореме о разгрузке остающиеся в теле деформации и напряжения равны разности их значений в истинном и фиктивном состоянии равновесия. Таким образом, в процессе формообразования вследствие упругого пружинения радиус кривизны увеличится до

 мм

Следовательно, увеличение радиуса волюты составит

 мм

Пружинение вследствие упругого восстановления металла при разгрузке непосредственно изменяет кривизну пластически изогнутого элемента. Изменение угла загиба является следствием изменения кривизны.

Допуская линейную зависимость изменения радиуса изгиба вследствие пружинения, и связывая ее прямой пропорциональностью с углом загиба θ, получаем фактическое значение угла гибки

.

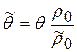1-й изогнутый участок волюты определяется углом загиба  градусов. Следовательно, пружинение уменьшит этот угол до

.

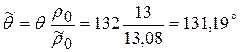Решая обратную задачу, определяем какой угол загиба нужно сообщить изделию в процессе формообразования, чтобы получить требуемое значение

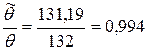 и угол загиба .

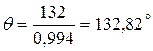Усилие формообразования при гибке представляет интерес с точки зрения определения потребной мощности и выбора соответствующего оборудования для осуществления данного процесса.

Усилие свободной гибки с учетом коэффициента трения  заготовки о формообразующий инструмент [3]

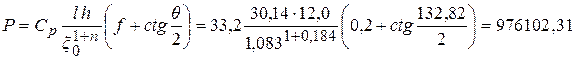 Н,

где:  — коэффициент, зависящий от механических свойств металла и ширины изгибаемой заготовки. При изгибе узких заготовок (объемное напряженное состояние)

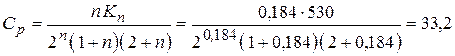 МПа;

l — длина линии изгиба прутковой заготовки. С учетом пружинения

 мм

Для остальных участков волюты, результаты расчета приведены в табл. 1.

Так как гибка волюты происходит последовательными участками, общее усилие операции будет определяться наибольшим усилием, характерным для 4-го участка

 Н (186748,1 кг).

Следует отметить, что приведенные здесь силовые параметры гибки справедливы для деформирования в холодном состоянии, т. е. применительно к условиям массового производства с использованием специализированного технологического оборудования. В случае ручного производства, усилие может быть значительно снижено ввиду нагрева заготовки в кузнечном горне и резкого уменьшения механических свойств материала.

Таблица 1.

Расчет участков волюты

Список литературы:
1.    Семерак Г., Богман К. Художественная ковка и слесарное искусство. — М.: Машиностроение, 1982 г. — 232 с.
2.    Навроцкий А.Г. Художественная ковка: учеб. пособие. — М.: Высш. школа, 1995. — 127 с.
3.    Лысов М.И. Теория и расчет процессов изготовления деталей методами гибки. — М. Машиностроение, 1966. — 236 с.