МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ О РЮКЗАКЕ

Введение.

В современном мире задача оптимальной загрузки или задача о рюкзаке, крайне актуальна, алгоритмы решения рюкзака применяются в криптографии, экономике, информатике, математике, вычислительной лингвистике, генетике и логистике. Применение алгоритмов решения рюкзака ещё больше расширяется за счёт того, что задача о рюкзаке является NP-полной, то есть к ней можно свести множество задач того же класса.

Исследованию задачи посвящено множество научных работ, так Silvano Martello и Paolo Toth написали книгу о своих изысканиях в этой области с названием “Knapsack Problem” (1990), пятью годами позднее Hans Kellerer, Ulrich Pferschy и David Pisinger публикуют одноимённую работу “Knapsack Problem”(1995). Не обошли стороной эту тему и российские исследователи, проблема об оптимальной загрузке упоминалась в книге С. Окулова «Программирование в алгоритмах», работе Б. Шнайдера «Прикладная криптография», учебнике В. Левитана «Алгоритмы: введение в разработку и анализ» и многих других публикациях.

Цель этой работы: найти самый оптимальный, быстрый и точный алгоритм для решения проблемы об оптимальной загрузке.

Задачи работы: найти и исследовать методы решения задачи об оптимальной загрузке на предмет скорости их реализации скорости их работы и объёму использованной памяти, провести их сравнительный анализ по этим критериям и выяснить, для каких условий оптимален каждый из методов.

Объектом исследования будут методы решения задачи, а предметом исследования разработанное мной приложения позволяющее провести сравнительную характеристику этих методов.

Методы, применяемые в работе — метод теоретического анализа, метод сравнения и эксперимент.

Структурно работа содержит две части. В первой приводится постановка задачи и классификация её вариантов и методов решения, а также характеристика каждого метода с описаниями алгоритма, его особенностей и затрат на его выполнение. Вторая часть включает в себя сравнительный анализ алгоритмов.

 Глава 1.          Методы решения задачи о рюкзаке.

Общая постановка задачи о рюкзаке звучит примерно так: как уложить вещи, каждая из которых имеет свой вес и свою стоимость, в рюкзак ограниченной вместимости по весу [1]. Существует шесть различных разновидностей задачи о рюкзаке.

·     Рюкзак 0—1;

·     ограниченный рюкзак;

·     неограниченный рюкзак;

·     рюкзак с мультивыбором;

·     мультипликативный рюкзак;

·     многомерный рюкзак.

Каждая из этих вариаций задачи служит разным целям и задачам и применяется в разных сферах. Так, неограниченны рюкзак может применяться в экономике для нахождения придельной выгоды при ограниченных ресурсах, а многомерный рюкзак для определения оптимальной загрузки транспорта, в то время как рюкзак 0—1 является основой криптосистемы Меркла-Хеллмана.

Рассмотрим подробней каждый вид этой задачи:

1.  Рюкзак 0—1.

Классическая задача о ранце, каждую вещь можно либо положить в рюкзак, либо нет. Все вещи в единственном экземпляре.

2.  Ограниченный рюкзак.

Каждую вещь можно взять ограниченное число раз. Другими словами, для загрузки доступно несколько конечных множеств однотипных вещей.

3.  Неограниченный рюкзак.

Каждую вещь можно взять неограниченное число раз. Количество вещей каждого типа значительно больше, чем может поместиться в рюкзак.

4.  Рюкзак с мультивыбором.

Все предметы делятся на определённые классы. Обязательным является условие выбора предмета из каждого класса.

5.  Мультипликативный рюкзак.

Имеется несколько рюкзаков с разной вместимостью необходимо максимизировать суммарную стоимость рюкзаков.

6.  Многомерный рюкзак.

Ограничений становится больше, то есть, например, не только вес, но и объём. В работе рассматриваются методы решения для классического варианта задачи, но все методы легко адаптируемы для всех типов задачи.

В данной работе будут исследованы различные алгоритмы для решения задачи о рюкзаке. Так как задача является NP-полной, то для неё нет полиномиального алгоритма, решающего задачу за разумное время. Поэтому приходится выбирать между точными, но медленными алгоритмами:

·     Метод простого перебора;

·     Метод ветвей и границ;

·     Динамическое программирование.

·     И неточными, но более быстрыми:

·     Жадный алгоритм;

·     Генетический алгоритм.

1.1                Метод простого перебора.

Самый тривиальный, но в то же время самый затратный по времени метод решения этой задачи. Временная сложность решения равна N!, то есть он работоспособен только для небольшого набора вещей. Его сложность равна O(N!).

Блок схема алгоритма решения задачи о рюкзаке методом простого перебора приведена на рис. 1.1.

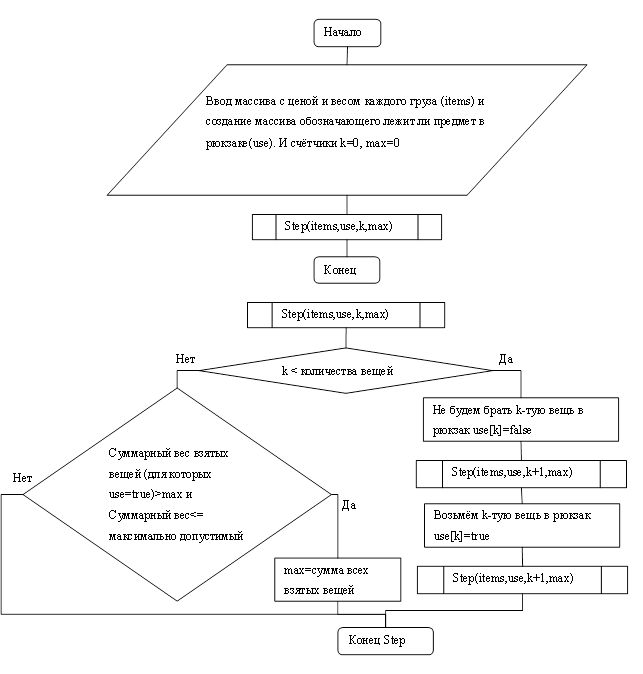
Рисунок 1.1. Блок-схема алгоритма простого перебора

1.2                Метод ветвей и границ.

По факту этот метод — это усовершенствованный метод перебора. Его отличие в том, что мы заранее отсекаем заведомо неверные варианты. Отсечение вариантов происходит следующим образом: Если какая-то вещь вызывает перегруз рюкзака, то не будем далее рассматривать ветку этого решения так как рюкзак будет перегружен. За счёт чего ускоряется решение задачи. Но в отдельных случаях он будет работать так же долго, как и полный перебор [2].

Рисунки 1.2 и 1.3 демонстрируют насколько уменьшится сложность перебора при использовании метода ветвей и границ.

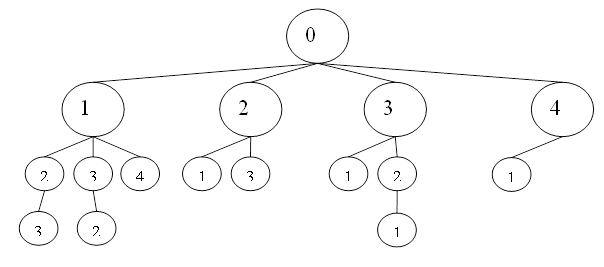
Рисунок 3. Схема перебора для метода ветвей и границ

1.3                Динамическое программирование.

Этот метод в программировании применяется довольно часто и заключается в следующем: изначально задача сильно упрощается, для нашей задачи, например, возьмём рюкзак ёмкостью 1 и всего 1 вещь. После чего будем увеличивать ёмкость рюкзака и смотреть какую максимальную цену мы можем получить. Потом добавляем 2 вещь и проделываем то же самое со 2-й вещью, учитывая результаты с первым грузом.

Для примера возьмём рюкзак вместимостью 13 (W=13) и пять вещей (N=5) (таблица 1.1):

Таблица 1.1.

Таблица вещей

Для иллюстрации работы динамического программирования составим таблицу 1.2.

Таблица 1.2.

Схема решения задачи о рюкзаке методом динамического программирования

Числа от 1 до 13 в первой строчке обозначают вместимость рюкзака k-вещи, которые мы берём. Для каждой клеточки мы считаем какая будет максимальная цена если мы попытаемся добавить к вышележащей клеточке k-ую вещь, учитывая ограничения рюкзака. И средняя сложность его равна O((W-1)*(N-1)*(N+1)/2) ≈ O(N*W).

Но этот алгоритм несёт в себе ещё один недостаток. Количество памяти необходимое для реализации алгоритма так же O(N*W), столько целочисленных ячеек необходимо для формирования таблицы.

1.4                Жадный алгоритм.

Суть этого алгоритма такова, для каждой вещи считаем коэффициент, который является отношением цены к его весу. Дальше берём те вещи, у которых этот коэффициент максимален и которые помещаются в рюкзак.

Рассмотрим пример с вещами из таблицы 1.4.

Таблица 1.4.

Пример набора вещей

Пусть вместимость рюкзака 5 единиц, тогда мы берём 1 груз, потом второй, потом пытаемся взять 3й, но не хватает места. Тогда суммарная стоимость рюкзака 10+6=16, но осталось 2 единицы свободного места. Если бы мы взяли вещи 2 и 3, то суммарная стоимость была бы 22 и свободного места не было бы. Именно поэтому Жадный алгоритм называется приближённым, он не всегда даёт правильный ответ.

Сортировка для последовательного выбора займёт O(N*log(N)) плюс проход по массиву. O(N*log(N))+O(N) но в общем случае O(N*log(N)) [4].

1.5                Генетический алгоритм.

Следующий алгоритм, на мой взгляд, самый неординарный. Суть алгоритма обращается к теории эволюции Чарльза Дарвина. А именно к её главной двигающей силе — естественному отбору. Введём некоторые термины:

Ген (Особь) — последовательность элементов логического типа длиной — равной количеству вещей. Каждому элементу соответствует одно значение: 1 — предмет взят или 0 — предмет не взят.

Популяция — совокупность нескольких особей.

Скрещивание (кроссинговер) — Обмен некоторыми частями двух генов (размер обмениваемых частей определяется случайно).

Пример: на рисунке 1.4 представлен возможные результаты скрещивания.

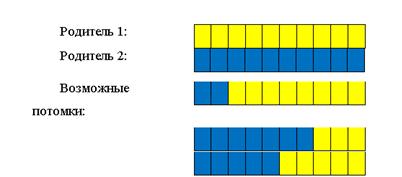
Рисунок. 1.4. Возможные результаты скрещивания

Мутация — случайное событие, которое случайным образом меняет одно значение на противоположное (учитывая переполнение рюкзака). На рисунке 1.5 представлен пример мутации:

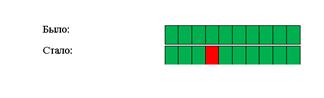
Рисунок 1.5. Пример мутации гена

Коэффициент полезности — некоторое значение, которое отображает, насколько данный ген приближен к ответу на задачу. В нашем случае это суммарная ценность одного гена (при условии, что рюкзак не переполняется).

Итак, суть алгоритма в следующем:

1.  Создаём начальную популяцию с помощью ДСЧ.

2.  Вычисляем коэффициент полезности для каждой особи.

3.  Специальным образом выбираем 2 особи для скрещивания (повторяем 5 раз). Специальный способ заключается в следующем, вероятность выбора каждого существа соответствует его коэффициенту полезности. Т. е. чем больше коэффициент полезности, тем выше вероятность того что это существо будет участвовать в скрещивании.

4.  Получаем несколько особей от каждого скрещивания (пять в нашем случае). Потом сортируем всех потомков и у случайных особей происходит мутация. После чего вновь считается коэффициент полезности для всех особей. Собираем всех существ (и родителей, и потомков) сортируем по коэффициенту полезности. Десять первых существ будут основой новой популяции. Далее повторяем со следующей популяцией действия с шага 1.

Подчеркнём некоторые принципы работы по этому методу:

·     На любом шаге следим, чтобы суммарный вес рюкзака был не больше максимального.

·     Продолжительность алгоритма зависит от ограничения по времени, но чем больше времени выделено на работу алгоритма, тем ближе результат алгоритма будет к искомому.

 Глава 2.          Сравнение методов.

Для исследования эффективности методов нужен был эффективный инструмент, который мог бы помочь в измерении эффективности программы. Такой инструмент был создан для данной работы. Представляет он собой программу, которая реализует каждый из алгоритмов.

2.1                Требования к программе.

Приложение должно быть интуитивно понятно, то есть реализовано в Windows forms. Необходимо предоставить удобный ввод для задания веса и цены каждой вещи. Необходимо реализовать проверку корректности ввода данных или ограничить ввод для корректности ввода.

2.2                Проектирование.

Для начала необходимо создать класс для хранения весов и цен каждой из вещей. Спроектированный класс (Item) представляет собой структуру с двумя значащими полями. Оба поля представлены большим целочисленным типом (BigInteger), этот тип предусматривает переполнение вследствие того, что в основе реализации этого типа лежит длинная арифметика.

Так же необходимо хранить решения. Каждое решение представлено последовательностью 0 и 1(как ранее упоминалось в части 1.4). Но кроме этого решение должно хранить суммарный вес и суммарную цену для этого решения. Класс Nabor состоит из массива логических переменных (по одной на каждую вещь) и два больших целых числа.

2.3                Пользовательский интерфейс.

Для ввода характеристик каждой вещи был выбран TextBox, на которые были наложены ограничения по вводу. Один TextBox для ввода весов, один для ввода цен, один для ввода ограничения рюкзака по весу. Так же нужна кнопка, которая будет запускать алгоритмы.

Для вывода результатов работы в приложении использовались label.

2.4                Сравнительная характеристика методов.

Для сравнительной характеристики программа была изменена для проверки на больших количествах вещей и больших числах. Это сделано для того, чтобы выполнить более точное сравнение по времени (на маленьких тестах слишком быстрое выполнение). На таблице 2.1 вы можете видеть статистику по 10 запускам программы со временем и правильностью ответа:

Таблица 2.1.

Результаты испытания на 10 тестах

Можно заметить, что генетически алгоритм отсутствует в эксперименте, он не был включён в эксперимент, так как его быстродействия ограничивается жёстко. Следовательно, тест на время проводить бессмысленно.

После проведения эксперимента и исследования всех вышеизложенных методов подведём итоги в таблице 2.2.

Таблица 2.2.

Сравнительная характеристика методов

Примечание: Память считается без хранения вещей и вместимости рюкзака (одинаковые у всех)

Объём памяти занимаемый временными переменными достаточно мал (относительно основного объёма) и примерно одинаков для всех алгоритмов

Заключение.

Рассмотренные алгоритмы различны по своей идее по своей реализации и степени надёжности. И соответственно, каждый алгоритм подходит к разным задачам или ТЗ. Так, Перебор может пригодиться тогда, когда нужно оперативное решение задачи, когда есть чуть больше времени можно улучшить перебор, превратив его в метод ветвей и границ (не забываем также, что это самые мало затратные по памяти способы). Если есть ещё больше времени и большей критике подвергается время выполнения, то оптимальным будет динамическое программирование. Если крайне критично время выполнения, но ответ не обязательно нужен лучший (просто какой-нибудь ответ, удовлетворяющий условиям и не последний по стоимости) то жадный алгоритм — это ваш выбор. Если же у вас есть время, но в будущем нужно будет искать ответ в определённых временных рамках то генетический алгоритм — это то, что вам нужно.

Список литературы:
1.    Окулов С. Программирование в алгоритмах. — М.: Бином. Лаборатория знаний, 2013. — 384 с.
2.    Левитин А. Алгоритмы: введение в разработку и анализ = Introduction to The Design and Analysis of Algorithms. М.: Вильямс, 2006. — 576 с.
3.    Martelo S., Toth P. Knapsack problems. J. Wiley & Sons, 1990. — 296 с.
4.    Лекция № 5 «Жадные алгоритмы» преподавателя МГИУ Беловой И. 2005. — 4 с.
5.    The knapsack problem // IFORS — [Электронный ресурс] — Режим доступа: http://www.ifors.ms.unimelb.edu.au/tutorial/knapsack/index.html [Проверено: 20.03.2014].