СРАВНЕНИЕ ДВУХ МЕТОДОВ ДЕКОДИРОВАНИЯ БЧХ КОДОВ, ИХ ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ В MathCAD

Основным средством обеспечения высокой помехоустойчивости большинства систем связи, особенно беспроводных, является корректирующее кодирование.

Широко используются в системах передачи данных циклические коды. Они реализованы в модемных протоколах передачи данных по телефонным сетям, в стандартах компьютерных сетевых технологий, в системе сигнализации ОКС-7, в стандарте сотовой связи GSM и т. д. В рассмотренных системах циклические коды используются в режиме обнаружения ошибок и последующего переспроса блока. Теория и реализация декодера, работающего в таком режиме достаточно просты.

При исправлении большого числа ошибок в блоке, особый интерес представляют коды БЧХ (Боуза-Чоудхури-Хоквингема), являющиеся подклассом циклических кодов.

Теория декодирования при исправлении ошибок значительно сложнее и базируется на арифметике полей Галуа.

Идея обнаружения ошибок в принятых сообщениях основана на передаче в составе блока данных избыточной служебной информации, по которой можно судить с некоторой степенью вероятности о достоверности принятых данных.

Коды БЧХ составляют мощный класс циклических кодов, которые обеспечивают достаточную свободу выбора длины блока, степени кодирования, размеров алфавита и возможностей коррекции ошибок.

Двоичные БЧХ коды с минимальным расстоянием 3, известные также как коды Хемминга, имели широкое применение в компьютерных сетях и устройствах памяти из-за простого и быстрого кодирования и декодирования. К примеру, укороченные (48,36,5) БЧХ коды использованы в Американской сотовой системе с временным разделением каналов (TDMA, стандарт IS-54).

Как сказано выше, вся теория декодирования БЧХ кодов основана на математических операциях в полях Галуа GF (). Использование данной арифметики в декодировании дает возможность упростить сложные комбинационные схемы реализации декодера.

Главная идея декодирования БЧХ кодов заключается в использовании примитивных элементов конечных полей для нумерации позиций кодового слова. Такая нумерация показана на рисунке 1 для вектора , соответствующего многочлену .

Рисунок 1. Нумерация позиций кодового слова элементами поля GF()

Синдромы определены как значения принятого полинома в нулях кода:

Введем многочлен ошибок локаторов ошибок

,                            (1)

корни которого равны обратным величинам локаторов ошибок. Тогда справедливо следующее соотношение между коэффициентами многочлена локаторов ошибок и синдромами:

                            (2)

Ключевое уравнение, представленное в (2), требует интенсивных вычислений в процедуре декодирования БЧХ кодов. На данный момент известны три основных метода решения уравнения (2):

1.  Алгоритм Берлекэмпа-Мэсси (BMA);

2.  Евклидов алгоритм (ЕА);

3.  Алгоритм Питерсона-Горенштейна-Цирлера (PGZ).

Нами изучены и реализованы в универсальной алгебраической среде MathCAD v.14 алгоритмы Евклида и PGZ для декодирования двоичных БЧХ. На рисунке 2 представлена блок-схема декодера двоичных БЧХ кодов.

Общий алгоритм декодирования двоичного БЧХ кода:

·     Вычислить синдромы, вычисляя значения принятого полинома в нулях кода

·     Найти коэффициенты многочлена локаторов ошибок

·     Найти обратные величины корней , т. е. позиции ошибок

·     Исправить принятое слово на вычисленных позициях для вычисленных значений ошибок.

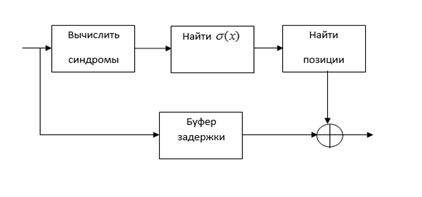
Рисунок 2. Схема двоичного БЧХ декодера

Для разработки данных алгоритмов в нашей работе мы использовали двоичный (15,7,5) код БЧХ, исправляющий две ошибки и порождаемый образующим многочленом .

Ниже мы представили блок-схемы исследуемых методов декодирования:

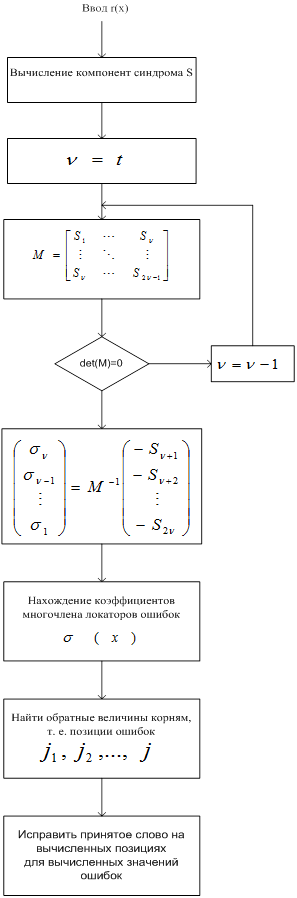
Рисунок 3. Декодер Питерсона-Горинштейна-Цирлера

Рисунок 4. Декодер, построенный по евклидову алгоритму

Для эффективной работы декодеров авторами созданы подпрограммы-функции для удобства программной реализации алгоритмов. В основном эти функции используются для интенсивных вычислений в конечных полях Галуа. К примеру: функция Sum (x,y) для сложения примитивных элементов в полях; Umn (x,y), осуществляющая умножение двух элементов; функция Obr2(x) для обращения элемента поля ; Qual (S), возвращающая степень элемента поля по двоичному представлению; функции  для вычисления определителей матриц 2*2 и 3*3; функция для обращения матрицы 2*2 Inv2(F);функция L(X,а) для определения значения уравнения при подстановке в него элемента поля; а также функция LE(X,a) для вычисления корней полинома локаторов ошибок. Uev(e,V), Svv(A,B),Svv2(A,B),deg(), DelVV(A,D) — функции, используемые для алгоритма Евклида.

По итогам работы видно, что оба алгоритма выполняют свою прямую функцию по исправлению любых одной и двух ошибок в искаженных кодовых комбинациях.

Список литературы:
1.    Р. Морелос-Сарагоса. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. Москва: Техносфера, 2005. — 320 с.
2.    Скляр Б. Цифровая связь. Теоретические основы и практическое применение. Изд. 2-е, испр.: Пер. с англ. — М.: Издательский дом «Вильнюс», 2003. — 1104 с.: ил. — Парал. тит. англ.
3.    Олифер В.Г., Олифер Н.А. Компьютерные сети. принципы, технологии, протоколы: Учебник для вузов. 3-е изд. — СПб.: Питер, 2007. — 958 с.: ил.
4.    Электронный курс по MathCAD — [Электронный ресурс] — Режим доступа. — URL: http://detc.ls.urfu.ru/assets/amath0021/frame.htm (Дата обращения 13.11.2014).