ДЕФОРМАЦИОННАЯ МОДЕЛЬ УТОНЕНИЯ ЛИСТОВОГО МАТЕРИАЛА ПРИ ВЫТЯЖКЕ ПУАНСОНОМ С РАЗЛИЧНОЙ ГЕОМЕТРИЕЙ ПРОФИЛЯ

Получение пространственных изделий путем сворачивания листового материала, является наиболее эффективным и производительным способом придания металлу требуемой формы. В этом отношении процесс листовой вытяжки успешно соперничает с литейным производством не только по стоимости производства, но по качеству металла отлитые детали уступают штампованным.

В настоящее время листовой вытяжке посвящено достаточное количество технической литературы и справочников, однако такие сопутствующие процессы при формоизменении заготовки, как развитие деформаций и изменение толщины стенки до сих пор до конца не исследованы.

С этой целью рассматривается деформационная модель утонения листового материала. Локализуемые в материале деформации изгиба, при втягивании круглой заготовки в штамп, обуславливают появление растянутых и сжатых слоев, разделяемых нейтральным радиусом . В результате давления слоев друг на друга и возникновения тангенциальных напряжений наружный радиус  будет уменьшаться до ; внутренний же радиус  увеличивается до  (рис. 1а).

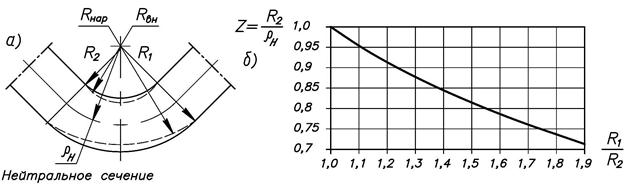
Рисунок 1. Формоизменение гнутого элемента (а) и положение нейтральной поверхности (б)

Используя равенство деформаций в растянутых и сжатых слоях, получаем следующую систему уравнений [1; 2].

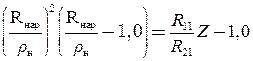;                                   (1а)

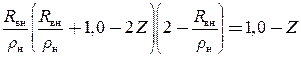,                         (1б)

где:  — коэффициент, определяющий положение нейтральной поверхности и вычисляемый из условия равновесия изгибающих моментов в растянутом и сжатом слоях заготовки:

.

С условием того, что процесс сворачивания изделия протекает с наличием трения по какой-либо поверхности, выражения изгибающих моментов могут включать дополнительный множитель, учитывающий контактное трение f [3]:

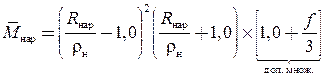;                           (2а)

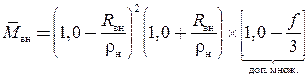.                               (2б)

Коэффициент нейтральной поверхности может быть установлен по расчетному графику, приведенному на рис. 1б, аппроксимация которого определяет зависимость ориентировочного нахождения искомого коэффициента [1]

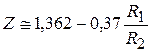.                                              (3)

Исследуем вытяжку цилиндрического стакана с целью установления закона изменения его толщины по основным элементам контура (рис. 2).

В качестве примера проведем расчет геометрических размеров вытягиваемого стакана Ø60×3 мм (D×S) при радиусе скругления пуансона  мм.

Рисунок 2. Профиль изделия

Для первой точки «1», обозначающей кромку изделия, отношение наружного и внутреннего радиусов

.

Коэффициент нейтральной поверхности (3)

.

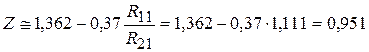Однако заявленное выражение не учитывает возмущающего фактора трения, определяющего незначительную корректировку найденного значения. Поэтому дополнительным итерационным перебором, из условия равновесия изгибающих моментов, уточняется  и согласно системе уравнений (1), значения деформированных радиусов

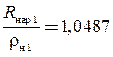 и .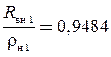

С учетом контактного трения только по наружной поверхности цилиндрической части стакана  (2а)

;

.

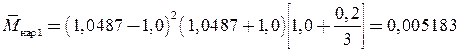Отличие моментов менее 1 % позволяет перейти к дальнейшему определению кинематических параметров гибки. Тогда нейтральный радиус

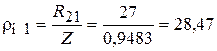 мм.

Деформированное значение наружного радиуса и толщина стакана на кромке в точке «1»

 мм;

 мм и .

Далее исследуем отношение размеров толщины для второй точки «2»

.

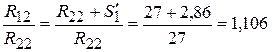При наличии технологического зазора между пуансоном и матрицей, превышающего толщину листового металла, контактное трение в данном сечении отсутствует, что позволяет предварительно определить (3)

, окончательно

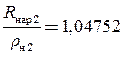;  и .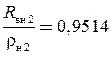

Относительные изгибающие моменты (без учета контактного трения)

 и  (отличие менее 1,0 %).

Тогда нейтральный радиус  мм.

Деформированное значение наружного радиуса и толщина стенки

 мм;

 мм и .

Сделаем аналогичные расчеты утонения и для точки сопряжения торового элемента с донышком. В этом случае расчетное отношение наружного и внутреннего радиусов в точке «3»

.

При отсутствии трения вследствие охвата материалом давящего инструмента — пуансона, относительные изгибающие моменты в растянутой и сжатой зонах

 и  (отличие менее 1,0 %).

Относительное положение нейтральной поверхност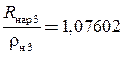и

 ;  и .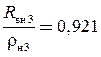

Тогда нейтральный радиус  мм.

Деформированное значение наружного радиуса

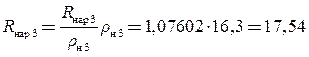 мм,

и толщина стенки

 мм и .

В рамках курсового и дипломного проектирования, в лаборатории кафедры «Машины и технологии обработки металлов давлением» Университета машиностроения (МАМИ), исследовалось сворачивание листовых меди и алюминия в цилиндрические стаканы различной высоты и диаметра. Соответствующие эксперименты производились на специальном вытяжном штампе, спроектированном и выполненном по оригинальным чертежам и позволяющим производить вытяжку листовых заготовок толщиной 2; 3; 4 мм при диаметре, соответственно 80; 110 и 140 мм (рис. 3). Подбор радиуса торцевого скругления сменных штемпелей пуансона, позволил получить изделия с требуемой кривизной донной части.

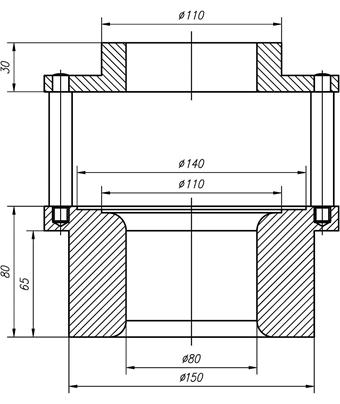
Рисунок 3. Вытяжной штамп

Исследование проводилось на трех плоских заготовках диаметром 110 мм и толщиной 3 мм из меди марки М1, деформируемых в стакан диаметром 60 мм пуансоном диаметром 53,4 мм с радиусом скругления кромки  мм (рис. 4а).

Продольно разрезав каждый стакан на две половинки, получаем 6 образцов по которым в дальнейшем строим выборку статистических расчетов утонения (рис. 4б). Для этого толщину каждого образца измеряем на различных участках, получая параллельные точки в левой (сечение А) и правой (сечение Б) частях одного образца, что вдвое увеличивает статистическую выборку (табл. 1).

Рисунок 4. Полученное изделие

Таблица 1.

Толщины образцов в различных сечениях

Статистическая обработка полученных данных производилась с вычислением среднего арифметического и среднего квадратичного отклонения (табл. 2).

Таблица 2.

Статистическая обработка данных

На основе сделанных расчетов, отмечается изменение толщины материала в процессе его деформации (рис. 4в). При этом средняя толщина материала в торовом скруглении

 мм.

Отличие от расчетного значения

.

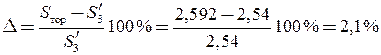Таким образом, отмечается удовлетворительная сходимость практических результатов с изложенной выше методикой определения величины утонения материала, что позволяет в дальнейшем использовать ее для практических расчетов при листовой вытяжке.

Так, например, уменьшение радиуса закругления кромки пуансона до минимальной величины для данной толщины материала  мм (), устанавливает ;  мм и . Аналогичные расчеты изменения толщины донной части рассматриваемой геометрии стакана, в зависимости от радиуса скругления пуансона, представлены в табл. 3.

Таблица 3.

Изменение толщины донной части стакана Ø60×3 мм

Графическое отображение проведенных расчетов представлено на рис. 5.

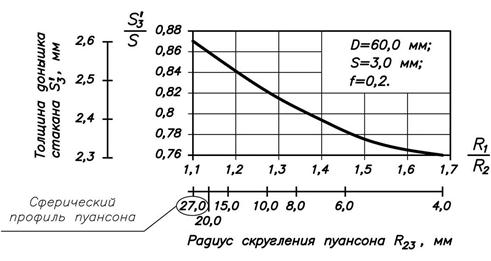
Рисунок 5. Изменение толщины донышка стакана

Таким образом, уменьшение радиуса скругления пуансона со сферического профиля до минимально возможного 4,0 мм, дополнительно увеличивает утонение донной части вытянутого изделия до 11,5 %.

Список литературы:
1.    Кохан Л.С., Лебедев Н.Н., Морозов Ю.А., Мочалов Н.А. Проектирование калибров сортовых станов и операций листовой штамповки. — М.: МГВМИ, 2007. — 340 с.
2.    Кохан Л.С., Морозов Ю.А. Исследование величины утонения при гибке // Современные инструментальные системы, информационные технологии и инновации. Материалы IX-ой Международной научно-практической конференции 22—23 марта 2012 года г. Курск. — Курск: ЮЗГУ, 2012. — С. 107—111.
3.    Кохан Л.С., Морозов Ю.А., Шульгин А.В. Изменение толщины стенок цилиндрических стаканов при вытяжке без прижима // Строительная механика инженерных конструкций и сооружений: обзорно-аналитический и научно-технический журнал. — М.: РУДН, 2014. — вып. 5. — С. 9—13.