ПРИМЕНЕНИЕ ТАБЛИЦЫ РЕШЕНИЙ ДЛЯ АВТОМАТИЗАЦИИ СЕЛЕКЦИИ ПО МНОЖЕСТВУ НЕЗАВИСИМЫХ ПРИЗНАКОВ

В настоящее время существует необходимость в автоматизации процесса селекции по множеству независимых признаков. К примеру, в животноводстве требуются средства для распределения особей в группы по различным качествам. Одним из способов являются таблицы принятия решений [2]. Такие таблицы позволяют в компактной форме установить связь между условиями и действиями. Как правило, таблицы разделяются на четыре части: Признаки, Наличие признака, Категории, Принадлежность к категории.

В первой части представленной одним столбцом записываются признаки, аналогично, во второй части таблицы записываются существующие категории. Остальные столбцы таблицы занимают 3 и 4 части. Третья часть содержит различные варианты состояний условий. Таким же образом в четвертой части записывается информация, какое действие выполнить.

В качестве примера использования таблицы принятия решений можно привести задачу распределения особей по категориям.

Имеется шесть категорий, они обозначены цифрами от 1 до 6. Так же определены признаки, по которым необходимо распределять особей.

Для распределения объектов по категориям программа должна проверить наличие признаков и выдавать на выходе принадлежность категориям. Так же следует отметить, что категории могут пересекаться и содержать более одного признака.

Очевидно, что для составления алгоритма программы, необходимо учесть все возможные комбинации признаков, что является весьма трудоемкой задачей, поскольку количество возможных вариантов будет равно 2ⁿ, где n — число признаков. Ниже представлена таблица решений, которая наглядно показывает все логические зависимости признаков и является наиболее общим описанием программы.

Таблица 1.

Таблица решений

Данный пример показывает простоту, с которой таблица решений показывает возможные варианты признаков и комбинации категорий. К тому же таблицу легко модифицировать при изменении исходных данных, например, при изменении требований к категориям.

Одним из способов обработки таблиц решений, является построение эквивалентного ей дерева решений (ДР). Для этого на основе таблицы решений строится система логических функций , где m — число признаков в таблице решений. Логическая функция представляется следующим образом:

                                                       (1)

где: переменная соответствующая наличию или отсутствию признака;

При этом , если наличие признака ; , если состояние условия  и буква  отсутствует в формуле, если состояние условия не имеет значения. Подробно алгоритм получения системы логических функций описан в [1].

Таблица решений является обобщённым представлением всех возможных деревьев решений, следует отметить, что уже при семи условиях, число возможных деревьев решений будет равно 19*10²⁶. Таким образом, поиск оптимального ДР путем полного перебора невозможен.

Основным фактором, влияющим на количество вершин, а, следовательно, и на число логических проверок, является порядок проверки переменных. Для определения порядка переменных в [1] предложен метод определения структурных характеристик системы логических функций, согласно которому первой выбирается переменная, входящая в наибольшее число логических функций системы. В таблице 2 представлены характеристики системы логических функций для таблицы решений в таблице 1.

Таблица 2.

Характеристики системы

ДР построенная согласно полученному порядку проверки переменных представлена на рис. 1. Число условных вершин: 11.

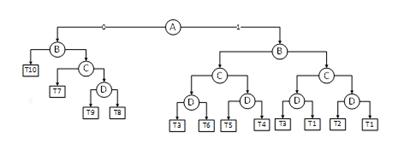
Рисунок 1. ДР с порядком проверки A> B> C> D

Как можно было заметить из таблицы 2, переменные C и D обладают равным числом вхождений. Поэтому, меняя местами эти переменные в порядке проверки состояний условий, можно получить ДР с большим числом вершин чем в диаграмме, представленной на рисунке 1. ДР с порядком проверки A> B> D> C представлена на рис. 2.

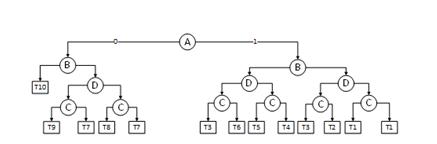
Рисунок 2. ДР с порядком проверки A> B> D> C

Как можно заметить, выбор из двух переменных с одинаковым числом вхождений влияет на результирующую диаграмму решений, следовательно, необходимо учитывать это влияние при выборе переменной. Как можно заметить, каждая переменная является корнем двух поддеревьев, а значит возможно определять порядок проверки переменных для каждого поддерева.

Для этого представим структуру системы логических функций в виде матрицы, следующего вида:

                                                                (2)

где: i — число переменных;

j — число функций.

Элемент  принимает следующие значения:

·     1, если в функции , для переменной , ;

·     0, если в функции , для переменной , ;

·     -1, если в функции , переменная отсутствует.

Матрица характеристик для таблицы решений процесса селекции представлена в табл. 3.

Таблица 3.

Структурные характеристики

Для определения порядка проверки переменных используется следующий алгоритм:

1.  Первой выбирается переменная, номер которой соответствует строке с наибольшей суммой числом неотрицательных элементов:

                                                                     (3)

где:  — сумма элементов строки

Если для двух переменных с номерами k и r, = то выбирается переменная с номером k, если k <r; r, если r<k

2.  Далее из исходной строятся левая и правая подматрицы:

·     Левая подматрица состоит из тех столбцов где , при этом k-ая строка вычеркивается.

·     Правая подматрица состоит из тех столбцов где , при этом k-ая строка вычеркивается.

·     После этого пункты 1 и 2 выполняются для каждой подматрицы.

Дерево решений, полученное в соответствии с определенным выше порядком проверки, будет выглядеть как на рис. 4

Рисунок 3. Асимметричное дерево решений

Как можно заметить, число вершин в дереве решений равно 9. Что позволит уменьшить количество логических проверок.

В данной статье рассмотрен алгоритм построения рационального дерева решений, где в качестве критерия используется уменьшение числа логических проверок. Так же критериями могут быть показатели, зависящие от конкретной области, например, стоимость проверки условия или вероятность появления определенных комбинаций. Однако, данные критерии требуют разработки дополнительных методов построения алгоритмов.

Так же на основе дерева решений легко строится программная реализация алгоритма, что позволяет создавать программы для автоматизации селекции.

Список литературы:
1.    Муромцев В.В. Методы синтеза логических схем: Учебное пособие. — 2-е изд., перераб. и доп. — Белгород: Изд-во БелГТАСМ, 2001. — 78 с.
2.    Хайнби Э. Программирование таблиц решений. — М.: Мир, 1976. — 89 с.