ПРИМЕНЕНИЕ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ В ПРОЦЕССЕ РЕШЕНИЯ ЗАДАЧ НА ОПТИМИЗАЦИЮ

В данной работе представлен подход к решению задач на оптимизацию в различных программных средствах и оценка данных программных средств с различной точки зрения.

        В настоящее время мировая экономика находится в кризисе, от которого в той или иной степени страдают практически все отрасли, такие как машиностроение, медицина, торговля т. д. Соответственно, одним из факторов выживания компании становится увеличение отдачи от бизнес-процессов, что подразумевает под собой увеличение эффективности работы каждого сотрудника, улучшение качества выпускаемой продукции, снижение всевозможных затрат. В связи с этим возникает потребность в оптимизации деятельности компании [2].

Вместе с тем XXI век — это век информационных технологий. Практически в каждом виде практической деятельности человека используются информационные и коммуникационные технологии, поэтому было бы целесообразно применять их и в процессе оптимизации, тем более что решение оптимизационных задач достаточно трудоемкий процесс, при реализации которого необходим учет большего количества параметров и возможно возникновение большего количества ошибок.

Для того чтобы решить задачу на оптимизацию с применением технических средств, необходимо построить математическую модель процесса, включающую в себя совокупность математических соотношений, описывающих суть задачи. Составление математической модели задачи линейного программирования состоит из следующих этапов:

·       выбор переменных задачи;

·       составление системы ограничений;

·       выбор целевой функции;

·       нахождение максимума или минимума полученной функции.

В приведенной ниже таблице представлены программные средства, обладающие возможностями их применения в процессе решения оптимизационных задач.

Таблица 1.

Программные средства для решения задач на оптимизацию

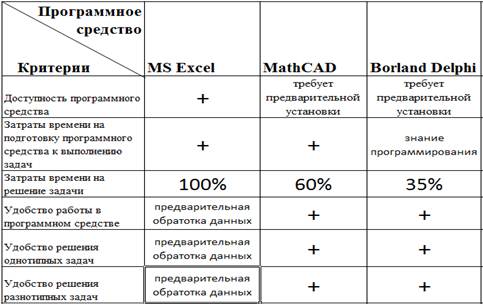
Кроме этого стоит отметить, что значительное влияние на выбор того или иного программного обеспечения оказывает не только его распространенность, но также скорость и удобство выполнения с его применением поставленной задачи.

Таблица 2.

Сравнительная оценка скорости и удобства работы в программных средствах MS Excel, MathCAD, Borland Delphi

В качестве примера решения задачи на оптимизацию я выбрал случайную задачу:

Для изготовления трех видов изделий А, В и С используется токарное, фрезерное, сварочное и шлифовальное оборудование. Затраты времени на обработку одного изделия для каждого из типов оборудования указаны в таблице. В ней же указан общий фонд рабочего времени каждого из типов используемого оборудования, а также прибыль от реализации одного изделия каждого вида [1].

На основе выше приведенного условия была составлена таблица 3 к данной задаче:

Таблица 3.

Табличный вариант условий задачи получения прибыли

Рассмотрим пример решения задачи на оптимизацию в программной среде MathCAD (Рис. 1), т. к. работа в этой среде, во-первых, использование данного средства не требует навыков программирования, а во-вторых, запись команд осуществляется значительно проще, чем в MS Excel.

Решение задачи будет состоять из следующих этапов:

1.  введение необходимого количества переменных и присваивание им начальных значений;

2.  применение вычислительного блока Given и задание ограничивающих условий в данном вычислительном блоке;

3.  применение функции максимума;

4.  вывод результата.

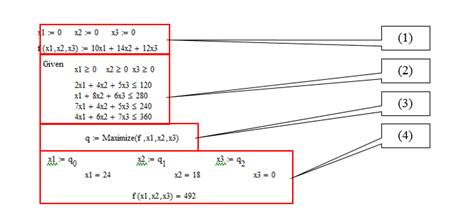
Рисунок 1 Пример решения задачи на оптимизацию в программном средстве MathCAD

Таким образом в данной работе рассмотрены программные средства, позволяющие решать задачи на оптимизацию, и представлен подход к решению одной из задач, заключающийся в применении программного средства MathCAD.

Список литературы:
1.    Задачи оптимального планирования — [Электронный ресурс] — Режим доступа. — URL: http://cl.rushkolnik.ru/docs/10078/index-611.html (дата обращения 17.03.2015)
2.    Планирование персонала на предприятии на примере УЧХОЗ ЗЕРНОВОЕ — [Электронный ресурс] — Режим доступа. URL: http://coolreferat.com/ (дата обращения 16.03.2015).