ИСПОЛЬЗОВАНИЕ АППАРАТА ЛИНЕЙНОЙ АЛГЕБРЫ ДЛЯ ОЦЕНКИ СИЛЫ СОПРОТИВЛЕНИЯ СРЕДЫ

Аппарат линейной алгебры, как правило, применяется к решению задач экономического содержания [3; 5]. Целью данной работы является применение методов решения систем алгебраических уравнений к моделированию и оценке силы сопротивления среды  движущемуся телу с использованием метода анализа размерностей [4; 6].

Размерность силы сопротивления

,

т.е. матрица размерности скорости  имеет вид:

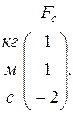
Предположим, от каких величин может зависеть искомая сила.

Очевидно, что сила  должна зависеть от скорости движения . Далее, логично предположить, что тела с большим поперечным сечением испытывают большее сопротивление, чем с меньшим. Поэтому в ответ должна войти площадь S поперечного сечения тела. И, наконец, сила  должна зависеть от параметра, характеризующего свойства среды.

Таких параметров два: плотность среды  и ее вязкость .

Проведем оценку силы сопротивления среды  в обоих случаях.

а)

Следуя [4], запишем искомую силу сопротивления в виде

,

где: a, b, g — показатели степени, которые необходимо определить.

Размерность выбранных величин  и матрица размерности записывается следующим образом:

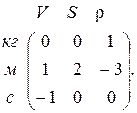
Тогда матричное уравнение для определения показателей степеней a, b, g имеет вид

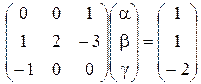, откуда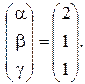

Таким образом,

,

т. е. в этом случае сила сопротивления среды пропорциональна квадрату скорости движения тела.

б)

Запишем искомую силу сопротивления в виде

,

где: a, b, g — показатели степени, которые необходимо определить.

Размерность выбранных величин  и матрица размерности записывается следующим образом:

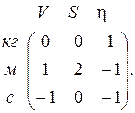
Матричное уравнение для определения показателей степеней a, b, g имеет вид

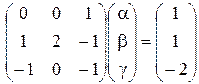, откуда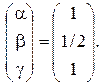

Таким образом,

,

т. е. в этом случае сила сопротивления среды пропорциональна скорости движения тела.

Полученные формулы для силы сопротивления  принципиально отличаются: в одной из них сила зависит от скорости квадратично, в другой — линейно. Поэтому вопрос о доминировании в каждой конкретной задаче двух процессов — лобового сопротивления или вязкости среды — остается открытым.

Для дальнейшего исследования включим в анализ размерности и плотность среды, и ее вязкость.

в)

Запишем искомую силу сопротивления в виде

,

где: a, b, g, δ — показатели степени, которые необходимо определить.

Размерность выбранных величин

и матрица размерности записывается следующим образом:

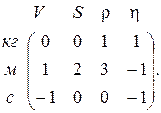
Тогда матричное уравнение для определения показателей степеней a, b, g, δ имеет вид:

.

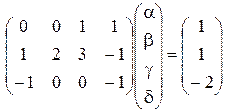Имеем систему трех уравнений с четырьмя неизвестными. Исследование совместности полученной системы проведем по методике [2, с. 40].

Приведем расширенную матрицу элементарными преобразованиями к ступенчатому виду:

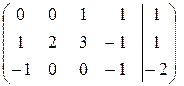
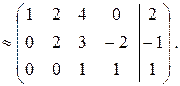
Очевидно, что ранги матрицы системы и расширенной матрицы совпадают и равны 3, т. е. система имеет множество решений.

За базисный возьмем угловой минор 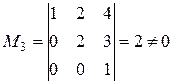, а за базисные переменные выберем неизвестные .

Исходная система приобретает вид: 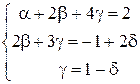, откуда по методу Гаусса находим решения: 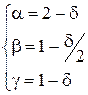, , следовательно,

Группируя входящие в правую часть уравнения величины, получим:

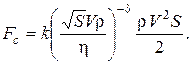
Комбинация величин в скобках стоит в произвольной степени  Это позволяет предположить, что эта комбинация безразмерна.

Действительно, .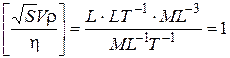

Этот безразмерный параметр в механике сплошных сред называют числом Рейнольдса Re [1, с. 67]:

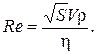
Число Рейнольдса может быть включено в безразмерную величину k, которая в этом случае оказывается не постоянной величиной, а функцией безразмерного параметра:

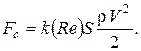
Он играет важную роль в определении характера силы сопротивления. График зависимость силы сопротивления от числа Рейнольдса представлен на рисунке 1 [1, с. 78].

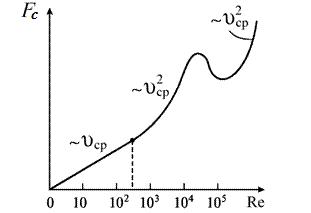
Рисунок 1. Зависимость силы сопротивления среды от числа Рейнольдса

Таким образом, при малых значениях чисел Рейнольдса воспроизводится выражение для силы сопротивления, полученное в п. б), а при больших — формула п. а).

Число Рейнольдса очень полезно с точки зрения моделирования потоков в различных жидкостях и газах, поскольку их поведение зависит не от реальной вязкости, плотности, скорости и линейных размеров элемента потока, а лишь от их соотношения, выражаемого числом Рейнольдса.

Благодаря этому можно, например, поместить в аэродинамическую трубу уменьшенную модель самолета и подобрать скорость потока таким образом, чтобы число Рейнольдса соответствовало реальной ситуации полномасштабного самолета в полете. Далее, можно модель самолета уменьшить в два раза, а скорость обтекания увеличить в два раза и от этого тоже ничего не изменится. И, наконец, можно вместо аэродинамической трубы использовать гидроканал. Расчеты показывают, если модель самолета испытать в воде со скоростью 7 км/час и в воздухе со скоростью 100 км/час, то результат будет одинаков.

Список литературы:
1.    Алешкевич В.А., Деденко Л.Г., Караваев В.А. Механика сплошных сред. — М.: Физический факультет МГУ, 1998. — 92 с.
2.    Демин С.Е., Демина Е.Л. Линейная алгебра. — Нижний Тагил: РИО НТИ (ф) УГТУ-УПИ, 2005. — 124 с.
3.    Кремер Н.Ш. Высшая математика для экономистов. — М.: Изд-во ЮНИТИ — ДАНА, 2007. — 471 с.
4.    Седов Л.И. Методы подобия и размерностей в механике. — М.: Наука, 1972. — 440 с.
5.    Сирл С., Госман У. Матричная алгебра в экономике. — М.: Статистика, 1974. — 288 с.
6.    Хантли Г. Анализ размерностей. — М.: Мир, 1970. — 174 с.