РЕШЕНИЕ МАТЕМАТИЧЕСКИХ ЗАДАЧ ПРИ ПОМОЩИ СИСТЕМЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ AUTOCAD
Секция: 10. Моделирование

XXIV Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
РЕШЕНИЕ МАТЕМАТИЧЕСКИХ ЗАДАЧ ПРИ ПОМОЩИ СИСТЕМЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ AUTOCAD
Линейная алгебра и векторная геометрия являются одними из основных предметов в учебных программах технических специальностей университетов. Продолжая школьную программу и формируя углубленный курс изучения, эти дисциплины затрагивают более сложные разделы математической науки.
Современная школа рассматривает предмет черчение, как предмет необязательный для изучения, поэтому у многих студентов плохо развито пространственное мышление, и, вследствие этого, они испытывают затруднения не только в работах по начертательной геометрии, но и в остальных учебных дисциплинах. Поэтому решение математической задачи, описанной ниже, может дополнительно осложняться неразвитым представлением сложных 3D-объектов.
Одним из основных разделов высшей математики является «Поверхности второго порядка», контрольно-проверочным заданием которого служат задачи на построение поверхности, образованной пересечением двух других или более. Решить подобную задачу можно алгебраически (получив уравнение этой поверхности и сравнив его с табличным), но более удобным и менее затратным по времени способом является моделирование данных объектов в среде, позволяющей выполнять 3D-построение.
Несмотря на то, что выполнить данную работу можно практически в любом графическом редакторе, позволяющем осуществлять 3D-моделирование, целесообразнее будет работать в «AutoCAD» — одной из самых распространенных САПР» [1, c. 3]. Для решения поставленной задачи требуются минимальные навыки владения средой AutoCAD.
Данная работа является результатом исследования студентов указанной специальности под руководством ведущего преподавателя. Были рассмотрены решения многих задач на пересечение поверхностей второго порядка. В данной работе представлено одно из них, как наиболее наглядное.
Нам была поставлена цель решить задачу, имеющую следующее условие: «Построить тело, ограниченное указанными поверхностями: z = 0; z = 2x; x = ![]() ; x + y = 2» [2, c. 145].
; x + y = 2» [2, c. 145].
Для облегчения построений и наглядного представления формы поверхности плоскости выполнены в цветном изображении. Выполнение построений начинается с введения осей OX, OY и OZ в окне 3D-моделирования, рис. 1.
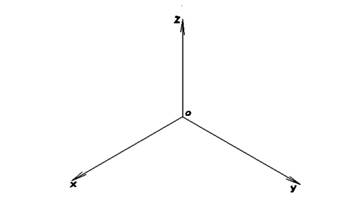
Рисунок 1. Ортогональный базис, заданный осями OX, OY и OZ
Затем вводится первая плоскость z = 0. Очевидно, что это плоскость, образованная пересечением осей OX и OY. Для ее построения выполняется команда «Плоская поверхность», рис. 2. Для облегчения построения каждую последующую плоскость можно убирать в отключенные слои.
Плоскость, заданная уравнением z = 2x, проходит через ось OY перпендикулярно плоскости XOZ, поэтому ее целесообразно построить по двум точкам, находящимся в плоскости XOZ.
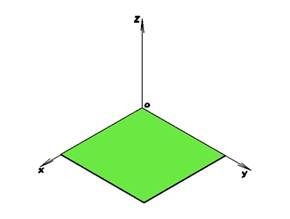
Рисунок 2. Построенная плоскость, заданная уравнением z = 0
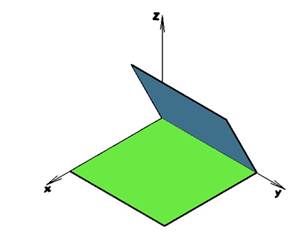
Рисунок 3. Построенная плоскость, заданная уравнением z = 2x
Пусть первая точка имеет координаты (0; 0; 0), а вторая (10; 0; 20). Построив их и соединив, получаем прямую, после чего, применив к этой прямой операцию «Выдавить», получаем необходимую плоскость, рис. 3.
Плоскость, заданная уравнением x = ![]() , проходит через ось OZ перпендикулярно плоскости XOY. График функции x =
, проходит через ось OZ перпендикулярно плоскости XOY. График функции x = ![]() — ветвь параболы, поэтому построение плоскости можно выполнить при помощи построения прямой, проходящей через три точки. Пусть первая точка имеет координаты (0; 0; 0), вторая (20; 40; 0), а третья (40; 160; 0). Соединив их командой «Сплайн» и применив к построенной прямой команду «Выдавить», получаем нужную плоскость, рис. 4.
— ветвь параболы, поэтому построение плоскости можно выполнить при помощи построения прямой, проходящей через три точки. Пусть первая точка имеет координаты (0; 0; 0), вторая (20; 40; 0), а третья (40; 160; 0). Соединив их командой «Сплайн» и применив к построенной прямой команду «Выдавить», получаем нужную плоскость, рис. 4.
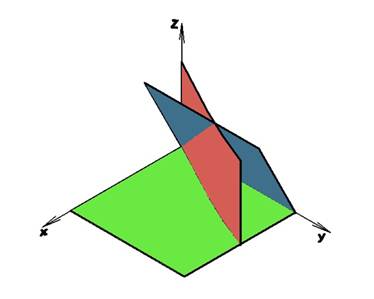
Рисунок 4. Построенная плоскость, заданная уравнением x = ![]()
Последняя плоскость x + y = 2 проходит параллельно оси OZ и перпендикулярно плоскости XOY. Ее построение аналогично построению двум предыдущим плоскостям. В качестве двух удобных точек подойдут: первая с координатами (20; 0; 0) и вторая (0; 20; 0), рис. 5.
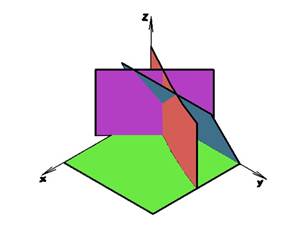
Рисунок 5. Построенная плоскость, заданная уравнением x + y = 2
Для всех плоскостей выполняется команда «Редактирование поверхности/обрезать». В результате можно наблюдать поверхность, образованную пересечением заданных плоскостей, рис. 6.
В результате разработки данной методики решения задач такого типа, студенты не только получают наглядное представление изображения полученной поверхности, но и при желании могут сами самостоятельно построить поверхность своего варианта. Выполнение такого задания способствует развитию пространственного воображения и закреплению знаний и навыков по изученной теме «Поверхности второго порядка».

Рисунок 6. Результат решения задачи
Представленный метод решения задачи дает возможность осуществить точную проверку выполненного задания как самими студентами, так и их преподавателями. Кроме того, студенты получают возможность развить качества, необходимые для будущей профессиональной деятельности в условиях высокой конкуренции на рынке труда согласно современным требованиям работодателей.
Список литературы:
1. Мохов И.С. Самоучитель. AutoCAD 2014. — [Электронный ресурс], 2014. — 68 с.
2. Рябушко А.П. Сборник индивидуальных заданий по высшей математике. Часть I. — Минск.: «Вышэйшая школа», 2014. — 271 с.
3. Сорокоумова Е.А. Педагогическая психология: Краткий курс. — Санкт-Петербург.: «Питер», 2009. — 176 с.





