РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ТРАНСФОРМАТОРОВ МЕТОДАМИ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ

В статье исследуются переходные процессы при подключении трансформаторов к сети операционными методами.

Переходный процесс, трансформатор, операционное исчисление.

При изменении режима работы трансформатора происходит переход от одного установившегося состояния к другому. Обычно этот переходной процесс длится небольшое время (доли секунды), однако он может сопровождаться весьма опасными для трансформатора явлениями. Рассмотрим, как протекают переходные процессы при подключении различных трансформатора к сети.

Задача 1. Пусть дан идеальный трансформатор с коэффициентом взаимоиндукции   и напряжением на входе . Определить выражения переходных токов.

Решение.

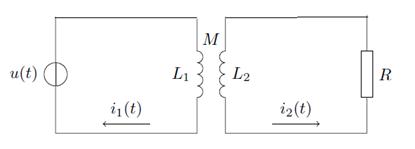
Дифференциальные уравнения Кирхгофа в данном случае имеют вид:

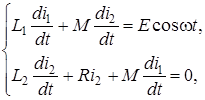 с начальными условиями

Используем для решения системы операционный метод [1–3].

Перейдем к изображениям:

Применим преобразование Лапласа к каждому уравнению системы:

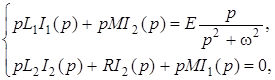
или

Решим полученную систему операторных уравнений по правилу Крамера:

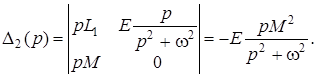
Так как трансформатор идеальный (), тогда

Осталось найти изображения неизвестных функций:

Искомые оригиналы имеют вид:

Задача 2. Рассмотрим теперь трансформатор без потерь с постоянной э.д.с. на входе , в обоих контурах которого включены емкости  и . Определим выражения переходных токов.

Решение.

Данная задача сводится к решению следующей системы уравнений:

с начальными условиями

Перейдем к изображениям:

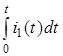
Применим преобразование Лапласа к каждому уравнению системы:

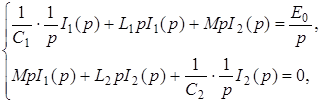
или

Решаем полученную систему операторных уравнений по правилу Крамера:

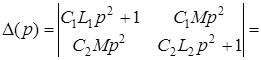
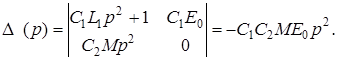
Найдем изображения неизвестных функций:

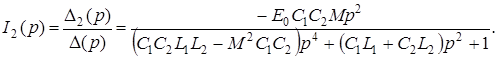
Для упрощения дальнейшего разложения биквадратного трехчлена в знаменателе на множители введем новые переменные:

Тогда

где были введены следующие обозначения:

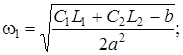
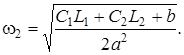
Теперь

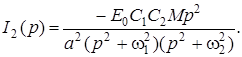
Используя теорему о свертке, найдем искомые оригиналы:

,

Список литературы:

1. Волков И.К. Интегральные преобразования и операционное исчисление: учеб. для вузов / И.К. Волков, А.Н. Канатников. – 2-е изд. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. – (Сер. Математика н техническом университете; Вып. XI).
2. Демин С.Е. Операционное исчисление: учеб. пособие / С.Е. Демин, Е.Л. Демина. – Нижний Тагил: НТИ (филиал) УрФУ, 2012.
3. Пантелеев А.В. Теория функций комплексного переменного и операционное исчисление в примерах и задачах: учеб. пособие / А.В. Пантелеев, А.С. Якимова. – М.: Высш. шк., 2001.